Formulieren Sie das Modell | Trial und Error | das Modell Solve

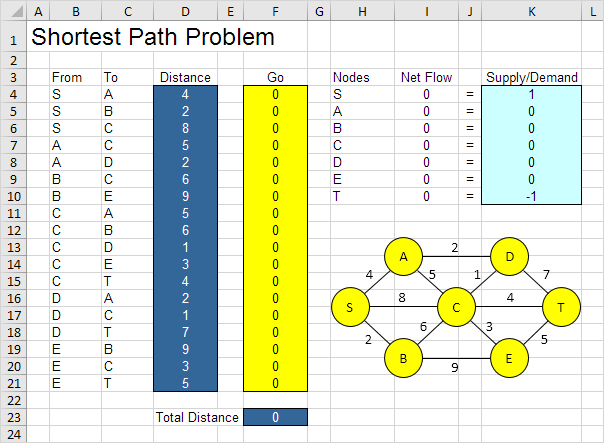
Verwenden Sie den Solver in Excel den kürzesten Weg von Knoten S zu Knoten T in einem ungerichteten Netzwerk zu finden. Punkte in einem Netzwerk werden als Knoten bezeichnet (S, A, B, C, D, E und T). Linien in einem Netzwerk genannt Bögen (SA, SB, SC, AC usw.).

Formulieren Sie das Modell

Das Modell werden wir Blicke zu lösen, wie in Excel folgt.

Shortest Path Problem in Excel

  1. Um dieses kürzesten Weg Problem zu formulieren, beantworten Sie die folgenden drei Fragen.

\ein. Was sind die Entscheidungen getroffen werden? Für dieses Problem müssen wir Excel, um herauszufinden, ob ein Lichtbogen auf dem kürzesten Weg ist oder nicht (Ja = 1, Nein = 0). Zum Beispiel, wenn SB Teil des kürzesten Weges ist, Zelle F5 gleich 1. Wenn nicht, Zelle F5 gleich 0

\ B. Was sind die Einschränkungen für diese Entscheidungen? Der Netto Flow (Flow Out – Durchfluss-In) jedes Knotens sollte auf Angebot / Nachfrage gleich sein. Knoten S sollte nur einen abgehenden Bogen (Net Flow = 1) hat. Knoten T sollte nur eine einlaufende Bogen hat (Nettofluss = -1). Alle anderen Knoten müssen eine abgehende Lichtbogen und einen einlaufenden Bogens, wenn der Knoten auf dem kürzesten Weg (Nettofluß = 0) oder keine Strömung (Nettofluß = 0) ist.

\ C. Wie hoch ist der Gesamtleistungsmaßstab für diese Entscheidungen? Das Gesamtmaß der Leistung ist die Gesamtstrecke des kürzesten Weges, so dass das Ziel ist, diese Menge zu minimieren.

  1. Um das Modell leichter zu verstehen, die folgenden Bereiche nennen.

Range Name

Cells

From

B4:B21

To

C4:C21

Distance

D4:D21

Go

F4:F21

NetFlow

I4:I10

SupplyDemand

K4:K10

TotalDistance

F23

  1. Legen Sie die folgenden Funktionen.

Insert Functions

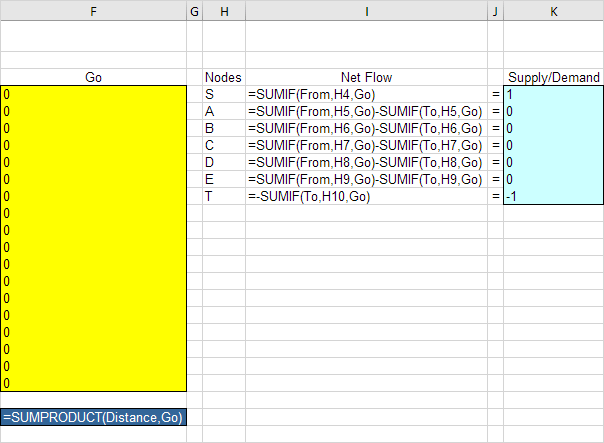
Erläuterung: Der SUMIF Funktionen berechnen den Nettofluss von jedem Knoten. Für Knoten S, fasst die SUMIF Funktion die Werte in der Go-Säule mit einem „S“ in der Spalte Von. Als Ergebnis nur Zelle F4, F5 oder F6 kann 1 (ein abgehender Bogen) sein. Für Knoten T summiert die SUMIF Funktion die Werte in der Go-Spalte mit einem „T“ in der Spalte Zu. Als Ergebnis kann nur Zellen F15, F18 oder F21 seine 1 (ein einlaufender Bogen). Für alle anderen Knoten, sieht Excel in der Von- und Bis-Spalte. Gesamtdistanz gleich die SUMPRODUCT von Entfernung und Go.

Trial and Error

Mit dieser Formulierung wird es einfach, jede Probelösung zu analysieren.

  1. Zum Beispiel hat der Pfad SBET eine Gesamtstrecke von 16

Trial Solution

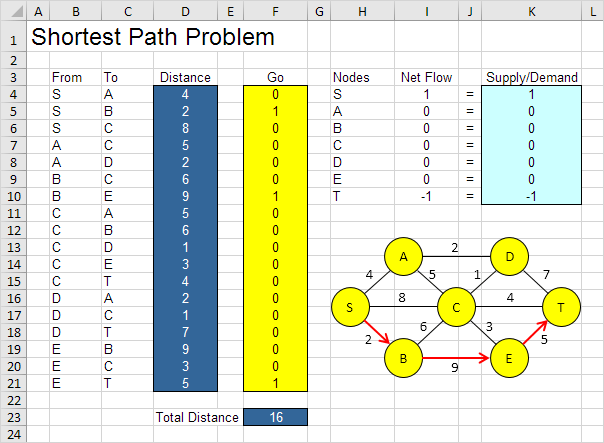
Es ist nicht zu verwenden Versuch und Irrtum notwendig. Wir werden als nächstes beschreiben, wie die Excel Solver schnell verwendet werden können, um die optimale Lösung zu finden.

Lösen Sie das Modell

Um die optimale Lösung zu finden, führen Sie die folgenden Schritte.

  1. Wählen Sie auf der Registerkarte Daten in der Gruppe Analyse auf Solver.

Click Solver

Hinweis: kann nicht die Solver-Taste finden? Klicken Sie hier, um das Add-In Solver zu laden.

Geben Sie den Solver-Parameter (weiter lesen). Das Ergebnis sollte mit dem Bild übereinstimmen.

Solver Parameters

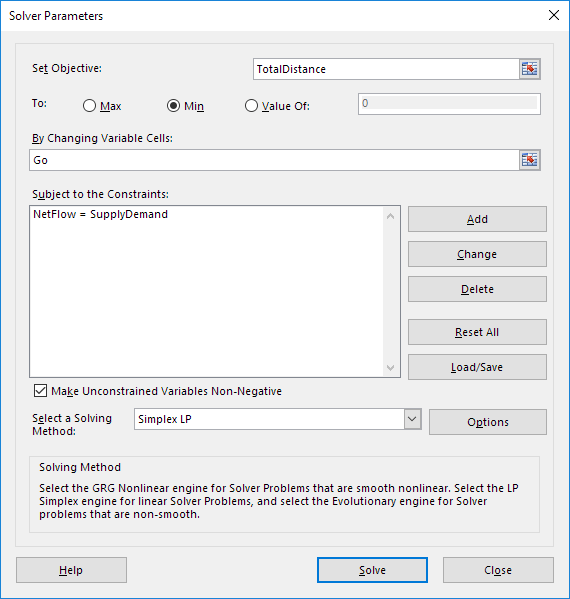
Sie haben die Wahl der Bereichsnamen eingeben oder in der Tabelle auf die Zellen klicken.

Geben Sie TotalDistance für die Ziel-2.

  1. Klicken Sie auf Min.

  2. Gehen Sie Geben Sie für die Änderung Variable Zellen.

  3. Klicken Sie auf Fügen Sie die folgende Einschränkung einzugeben.

Net Flow Constraint

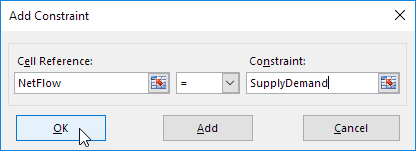
  1. Überprüfen ‚Make Unconstrained Variablen Non-Negative‘ und wählen Sie ‚Simplex LP‘.

  2. Klicken Sie abschließend lösen.

Ergebnis:

Solver Results

Die optimale Lösung:

Shortest Path Problem Result

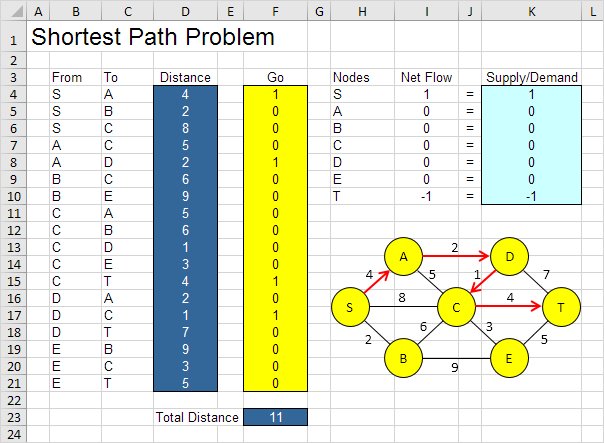
Fazit: SADCT ist der kürzeste Weg mit einer Gesamtstrecke von 11