Wie Korrelationskoeffizient in Excel finden
Was ist der Korrelationskoeffizient?
Der Korrelationskoeffizient eines Datensatzes ist eine statistische Zahl, die angibt, wie stark zwei Variablen miteinander in Beziehung stehen. Man kann sagen, dass dies der Prozentsatz der Beziehung zwischen zwei Variablen (x und y) ist. Es kann nicht größer als 100% und kleiner als -100% sein.
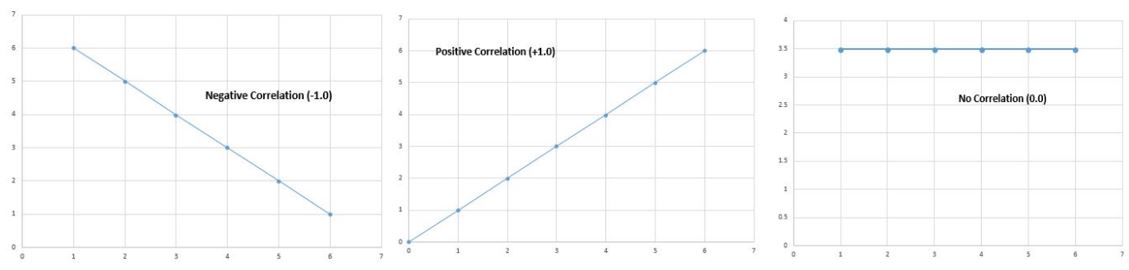
Der Korrelationskoeffizient liegt zwischen -1,0 und +1,0.
Ein negativer Korrelationskoeffizient sagt uns, dass wenn eine Variable zunimmt, die andere Variable abnimmt. Eine Korrelation von -1,0 ist eine perfekte negative Korrelation. Dies bedeutet, dass wenn x um 1 Einheit zunimmt, y um 1 Einheit abnimmt.
Ein positiver Korrelationskoeffizient sagt uns, dass wenn der Wert einer Variablen zunimmt, auch der Wert einer anderen Variablen zunimmt. Dies bedeutet, dass wenn x um 1 Einheit zunimmt, y auch um 1 Einheit zunimmt.
Die Korrelation von 0 besagt, dass es überhaupt keine Beziehung zwischen zwei Variablen gibt.
Die mathematische Formel des Korrelationskoeffizienten lautet:
Deckung ~ xy ~ / (Std ~ x ~ * Std ~ y ~)
Coveriance ~ xy ~ ist die Kovarianz (Stichprobe oder Population) des Datensatzes.
Std ~ x ~ = Es ist die Standardabweichung (Stichprobe oder Population) von Xs.
Std ~ y = ~ Es ist die Standardabweichung (Stichprobe oder Population) von Ys.
Wie berechnet man den Korrelationskoeffizienten in Excel?
Wenn Sie die Korrelation in Excel berechnen müssen, müssen Sie die mathematische Formel nicht verwenden. Sie können diese Methoden verwenden. Berechnung des Korrelationskoeffizienten mit der COREL-Funktion.
-
Berechnung des Korrelationskoeffizienten mit dem Analysis Toolpak.
Sehen wir uns ein Beispiel an, um den Korrelationskoeffizienten in Excel zu berechnen.
Beispiel für die Berechnung des Korrelationskoeffizienten in Excel Hier habe ich einen Beispieldatensatz. Wir haben xs im Bereich A2: A7 und ys im Bereich B2: B7.
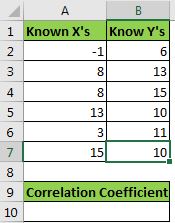
Wir müssen den Korrelationskoeffizienten von xs und ys berechnen.
Verwenden der Excel CORREL-Funktion
Syntax der CORREL-Funktion:
|
=CORREL(array1,array2) |
array1: * Dies ist der erste Satz von Werten (xs)
array2: * Dies ist der zweite Wertesatz (ys).
Hinweis: Array 1 und Array 2 sollten dieselbe Größe haben.
Verwenden wir die CORREL-Funktion, um den Korrelationskoeffizienten zu erhalten. Schreiben Sie diese Formel in A10.
|
=CORREL(A2:A7,B2:B7) |
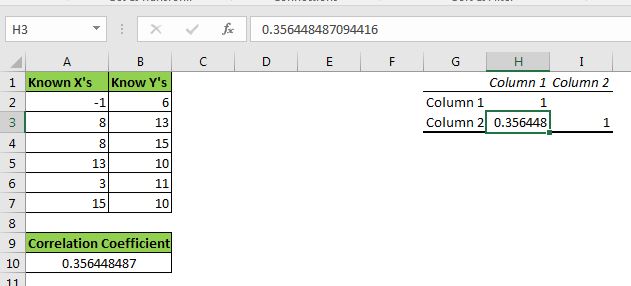
Wir erhalten eine Korrelation von 0,356448487 oder 36% zwischen x und y.
Verwenden des Excel Analysis Toolpak
Gehen Sie folgendermaßen vor, um die Korrelation mit dem Analyse-Toolpaket zu berechnen:
-
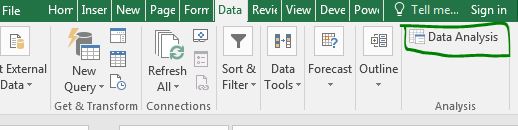
Wechseln Sie in der Multifunktionsleiste zur Registerkarte Daten. In der linken Ecke finden Sie die Option zur Datenanalyse. Klick es an. Wenn Sie es nicht sehen können, müssen Sie zuerst „verlinken: / tips-the-analysis-toolpak-in-excel [Analyse-Toolpak installieren]“.
-
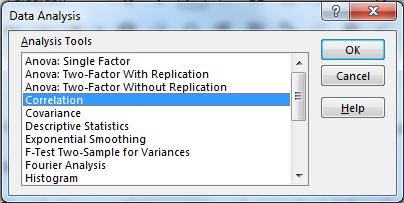
Wählen Sie aus den verfügbaren Optionen Korrelation aus.
-
Wählen Sie den Eingabebereich als A2: B7. Wählen Sie den Ausgabebereich aus, in dem Sie Ihre Ausgabe sehen möchten.
-
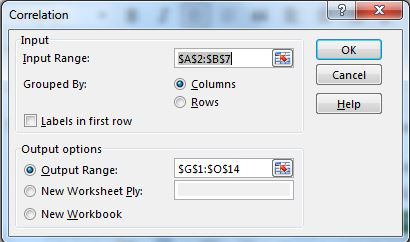
Klicken Sie auf OK. Sie haben Ihren Korrelationskoeffizienten im gewünschten Bereich. Dies ist genau der Wert, der von der CORREL-Funktion zurückgegeben wird.
How correlation is being calculated?* To understand how we are getting this value, we need to find it manually. This will clear our doubts.
Wie wir wissen, ist der Korrelationskoeffizient:
Deckung ~ xy ~ / (Std ~ x ~ * Std ~ y ~)
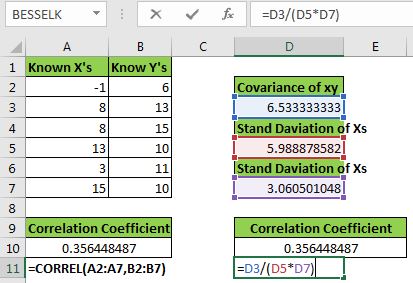
Zuerst müssen wir die Kovarianz berechnen. Wir können die COVERIACE.S-Funktion von Excel verwenden, um sie zu berechnen.
|
=COVARIANCE.S(A2:A7,B2:B7) |
Als nächstes berechnen wir die Standardabweichung von x und y mit dem STDEV.S
Funktion.
|
= |
|
= |
Schreiben Sie nun in Zelle D10 diese Formel.
|
=D3/(D5*D7) |
Dies entspricht = Kovarianz ~ xy ~ / (Std ~ x ~ * Std ~ y ~). Sie können sehen, dass wir genau den gleichen Wert erhalten, den die CORREL-Funktion angibt. Jetzt wissen Sie, wie wir den Korrelationskoeffizienten in Excel abgeleitet haben.
Hinweis: * Im obigen Beispiel haben wir COVARIANCE.S (Kovarianz der Stichprobe) und `link: / statistische Formeln-wie-verwendet-stdev-s-Funktion-in-Excel [STDEV.S] verwendet. `
(Standardabweichung der Probe). Der Korrelationskoeffizient ist der gleiche, wenn Sie COVARIANCE.P und link: / statistische Formeln-wie-verwenden-Excel-stdev-p-Funktion [STDEV.P] verwenden. Solange beide derselben Kategorie angehören, gibt es keinen Unterschied. Wenn Sie COVARIANCE.S (Kovarianz der Stichprobe) und link: / static-formulas-how-to-use-excel-stdev-p-function [STDEV.P]
verwenden (Standardabweichung der Grundgesamtheit) Dann ist das Ergebnis anders und falsch .__ Also Leute, so können wir den Korrelationskoeffizienten in Excel berechnen. Ich hoffe, dies war erklärend genug, um den Korrelationskoeffizienten zu erklären. Sie können jetzt Ihren eigenen Korrelationskoeffizientenrechner in Excel erstellen.
Verwandte Artikel:
link: / statistische-formeln-berechnen-abfangen-in-excel [INTERCEPT in Excel berechnen]
link: / statistische-formeln-berechnen-Steigung-in-Excel [Berechnung der Steigung in Excel]
link: / tips-regression-data-analyse-tool [Regressionen in Excel]
link: / statistische-formeln-wie-man-ein-standard-abweichungs-graph-in-excel erstellt [wie man einen Standard-Abweichungsgraphen erstellt]
link: / tips-descriptive-statistics [Beschreibende Statistik in Microsoft Excel 2016]
link: / statistische-formeln-wie-man-die-excel-normdist-funktion benutzt [wie man die Excel-NORMDIST-Funktion benutzt]
link: / tips-how-to-create-a-pareto-chart-in-microsoft-excel [Pareto-Diagramm und -Analyse]
Beliebte Artikel:
link: / Tastatur-Formel-Verknüpfungen-50-Excel-Verknüpfungen-zur-Steigerung-Ihrer-Produktivität [50 Excel-Verknüpfung zur Steigerung Ihrer Produktivität]
link: / formeln-und-funktionen-einführung-der-vlookup-funktion [Die VLOOKUP-Funktion in Excel]
link: / tips-countif-in-microsoft-excel [COUNTIF in Excel 2016]
link: / excel-formel-und-funktion-excel-sumif-funktion [Verwendung der SUMIF-Funktion in Excel]