Wie die Z.TEST Funktion in Excel verwenden
In diesem Artikel erfahren Sie, wie Sie die Z.TEST-Funktion in Excel verwenden.
Was ist Hypothesentest und wie wird Z-Test zum Testen von Hypothesen verwendet? In der Statistik wird der Hypothesentest verwendet, um die Schätzung des Mittelwerts für den Populationsdatensatz unter Verwendung der unterschiedlichen Verteilungsfunktion basierend auf dem Teil des Populationsdatensatzes mit dem Namen Beispieldatensatz zu ermitteln. Eine statistische Hypothese, manchmal auch als bestätigende Datenanalyse bezeichnet, ist eine Hypothese, die auf der Grundlage der Beobachtung eines Prozesses überprüft werden kann, der über eine Reihe von Zufallsvariablen modelliert wird. Es gibt zwei Arten von Hypothesen. Eine ist die Nullhypothese, die die behauptete Aussage ist, und die andere ist die alternative Hypothese, die der Nullhypothese genau entgegengesetzt ist. Wenn wir zum Beispiel sagen, dass die maximale Grenze für Blei in einem Maggi-Paket 225 ppm (parts per million) nicht überschreiten darf und jemand behauptet, dass es mehr als eine feste Grenze gibt als die Nullhypothese (bezeichnet mit U ~ 0 ~) und die alternative Hypothese (bezeichnet) von U ~ a ~)
U ~ 0 ~ = Bleigehalt im Maggi-Paket ist größer oder gleich 225 ppm. U ~ a ~ = Bleigehalt im Maggi-Paket beträgt weniger als 225 ppm.
Die obige Hypothese ist also ein Beispiel für einen rechtsseitigen Test, da die zugrunde liegende Situation auf der rechten Seite der Verteilungskurve liegt.
Wenn die zugrunde liegende Situation auf der linken Seite liegt, wird dies als Test mit linkem Schwanz bezeichnet. Nehmen wir noch ein Beispiel, das einen einseitigen Test veranschaulicht. Zum Beispiel, wenn Selina sagt, dass sie durchschnittlich 60 Liegestütze machen kann. Nun könnten Sie diese Aussage bezweifeln und versuchen, die Situation im Statistikbegriff zu hypothetisieren. Dann ist die Null- und die alternative Hypothese unten angegeben. U ~ 0 ~ = Selina kann 60 Liegestütze machen. U ~ a ~ = Selina kann nicht 60 Liegestütze machen. Dies ist eine Zwei -Tailed Test, bei dem die zugrunde liegende Situation auf beiden Seiten der beanspruchten Aussage liegt. Diese gezielten Tests wirken sich auf das Ergebnis der Statistik aus. Wählen Sie also die Null- und Alternativhypothese sorgfältig aus.
Z-Test Ein Z-Test ist ein statistischer Test, für den die Verteilung der Teststatistik unter der Nullhypothese durch eine Normalverteilung angenähert werden kann. Der Z-Test testet den Mittelwert einer Verteilung, in der wir die Populationsvarianz bereits kennen. Aufgrund des zentralen Grenzwertsatzes sind viele Teststatistiken für große Stichproben ungefähr normal verteilt. Es wird angenommen, dass die Teststatistik eine Normalverteilung aufweist, z. B. sollte die Standardabweichung bekannt sein, damit ein genauer Z-Test durchgeführt werden kann. Zum Beispiel möchte ein Anleger testen, ob die durchschnittliche tägliche Rendite einer Aktie größer als 1% ist, und kann mit dem Z-Test bewertet werden. Eine Z-Statistik oder ein Z-Score * ist eine Zahl, die angibt, wie viele Standardabweichungen über oder unter der mittleren Grundgesamtheit ein aus einem Z-Test abgeleiteter Score ist. Mathematisch entscheiden wir zuerst die Nullhypothese und berechnen den Z-Score für die Verteilung unter Verwendung der Formel.
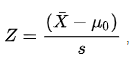
Hier ist X (mit einem Balken) der Mittelwert des Stichprobenarrays. U ~ 0 ~ ist der geschätzte Populationsmittelwert. S ist die Standardabweichung, wobei s gleich std / (n) ^ 1/2 ^ ist (wobei n die Stichprobengröße ist.) .
Wie oben angegeben, folgt der Z – Test der Standardnormalverteilung. Mathematisch folgt es in Excel der folgenden Formel.
Z.TEST (Array, x, Sigma) = 1 – Norm.S.Dist ((Durchschnitt (Array) – x) / (Sigma / (n) ^ 1/2 ^), WAHR)
oder wenn Sigma weggelassen wird:
Z.TEST (Array, x) = 1- Norm.S.Dist ((Durchschnitt (Array) – x) / (STDEV (Array) / (n) ^ 1/2 ^), TRUE)
Dabei ist x der Mittelwert der Stichprobe (Array) und n COUNT (Array).
Lassen Sie uns lernen, wie Sie den Z-Test mit der Z.TEST-Funktion durchführen, um die Beziehung zwischen den beiden angegebenen Datensätzen (tatsächlich und beobachtet) zu berechnen.
Z.TEST Funktion in Excel
Die Z.TEST-Funktion gibt die Wahrscheinlichkeit zurück, dass der Stichprobenmittelwert größer ist als der Durchschnitt der Beobachtungen im Datensatz (Array). Die Funktion akzeptiert die folgenden Argumente.
Z.TEST Funktionssyntax für eine Endwahrscheinlichkeit:
|
=Z.TEST ( array , x , [sigma] ) |
Die Funktion kann auch verwendet werden, um die zweiseitige Wahrscheinlichkeit umzuwandeln.
Z.TEST Funktionssyntax für eine Endwahrscheinlichkeit:
|
=2 * MIN(Z.TEST ( array , x , [sigma] ), 1-Z.TEST ( array , x , [sigma] ) ) |
Array: Beispieldatenverteilung x: Wert, für den der z-Test ausgewertet wird [Sigma] *: [optional] Die Populationsstandardabweichung (bekannt). Wenn nicht angegeben, wird die Standardabweichung der Stichprobe verwendet.
Beispiel:
All dies könnte verwirrend zu verstehen sein. Lassen Sie uns anhand eines Beispiels verstehen, wie die Funktion verwendet wird. Hier haben wir einen Beispieldatensatz Sales und wir müssen die Z-Testwahrscheinlichkeit für den gegebenen hypothetischen Populationsmittelwert unter der Annahme eines Endtests ermitteln.
Verwenden Sie die Formel:
|
= Z.TEST( A2:A9 , C3 ) |
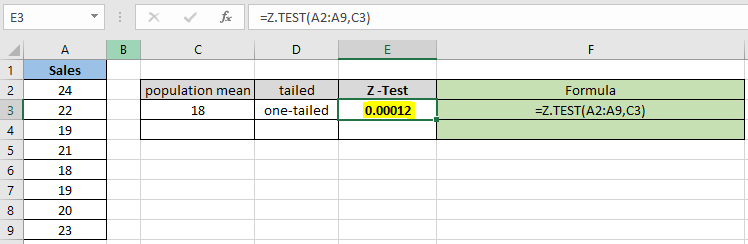
Der Wahrscheinlichkeitswert wird dezimal angegeben, sodass Sie den Wert in Prozent umwandeln können, indem Sie das Format der Zelle in Prozent ändern.
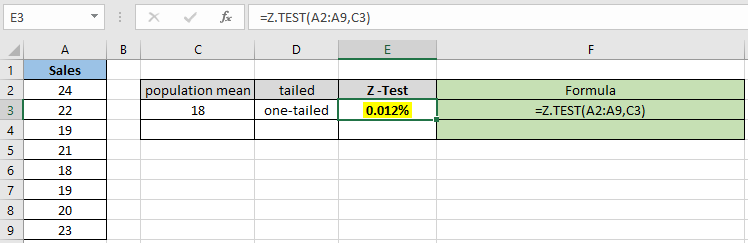
Wie Sie sehen können, beträgt der Wahrscheinlichkeitswert für den hypothetischen Populationsmittelwert 18 0,012% für die einseitige Verteilung. Berechnen Sie nun die Wahrscheinlichkeit unter der Annahme von zwei Endverteilungen mit denselben Parametern.
Verwenden Sie die Formel:
|
= 2 * MIN( Z.TEST(A2:A9,C4) , 1 – Z.TEST(A2:A9,C4) ) |
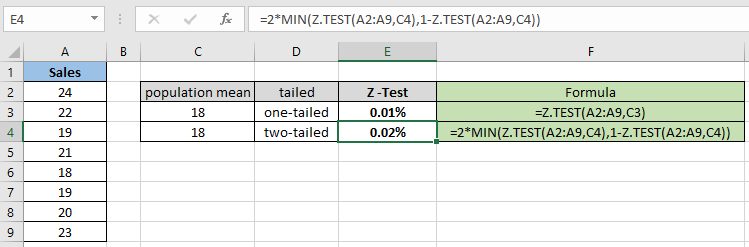
Für die zweiseitige Verteilung wird die Wahrscheinlichkeit für denselben Beispieldatensatz verdoppelt. Daher ist es notwendig, die Nullhypothese und die Alternativhypothese zu überprüfen. Berechnen Sie nun die Wahrscheinlichkeit für den unterschiedlichen hypothetischen Populationsmittelwert und eine Schwanzverteilung.
Verwenden Sie die Formel:
|
= Z.TEST( A2:A9 , C5 ) |
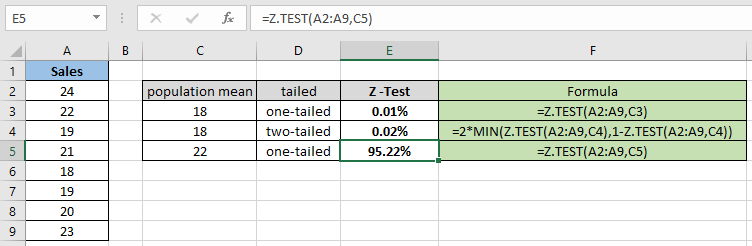
Wie Sie sehen können, beträgt der Wahrscheinlichkeitswert für den hypothetischen Populationsmittelwert 22 für die einseitige Verteilung 95,22%. Berechnen Sie nun die Wahrscheinlichkeit unter der Annahme von zwei Endverteilungen mit denselben Parametern.
Verwenden Sie die Formel:
|
= 2 * MIN( Z.TEST(A2:A9,C6) , 1 – Z.TEST(A2:A9,C6) ) |
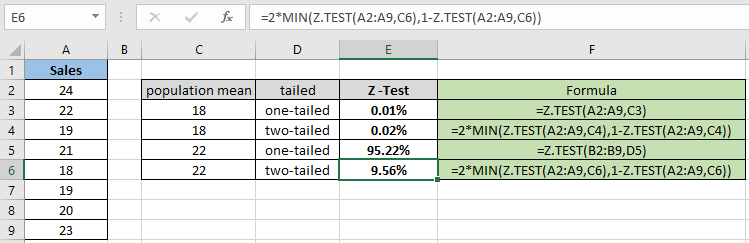
Da Sie von der obigen Momentaufnahme abweichen können, wird der Wahrscheinlichkeitswert bei der Berechnung der zweiseitigen Verteilung geringer. Die Funktion gibt 9,56% für den hypothetischen Populationsmittelwert 22 zurück.
Z.TEST stellt die Wahrscheinlichkeit dar, dass der Stichprobenmittelwert größer als der beobachtete Wert AVERAGE (Array) ist, wenn der zugrunde liegende Populationsmittelwert 0 ist. Aus der Symmetrie der Normalverteilung ergibt sich, wenn AVERAGE (Array) <x, Z.TEST Geben Sie einen Wert größer als 0,5 zurück.
Hier finden Sie alle Beobachtungsnotizen, die die Z.TEST-Funktion in Excel verwenden
Hinweise:
-
Die Funktion funktioniert nur mit Zahlen. Wenn der Populationsmittelwert oder das Sigma-Argument nicht numerisch ist, gibt die Funktion #VALUE zurück! Error.
-
Der Wert in Dezimalzahl oder der Wert in Prozent entspricht dem Wert in Excel.
Konvertieren Sie den Wert bei Bedarf in Prozent.
-
Die Funktion gibt #NUM zurück! Fehler, wenn das Sigma-Argument 0 ist.
-
Die Funktion gibt # N / A zurück! Fehler, wenn das bereitgestellte Array leer ist.
-
Die Funktion gibt # DIV / 0 zurück! Fehler, .. Wenn die Standardabweichung des Arrays 0 ist und das Sigma-Argument weggelassen wird.
-
Wenn das Array nur einen Wert enthält.
-
Hoffe, dieser Artikel über die Verwendung der Z.TEST-Funktion in Excel ist erklärend. Weitere Artikel zu statistischen Formeln und verwandten Excel-Funktionen finden Sie hier. Wenn Ihnen unsere Blogs gefallen haben, teilen Sie sie Ihren Freunden auf Facebook mit. Und Sie können uns auch auf Twitter und Facebook folgen. Wir würden gerne von Ihnen hören, uns mitteilen, wie wir unsere Arbeit verbessern, ergänzen oder innovieren und für Sie verbessern können. Schreiben Sie uns unter [email protected].
Verwandte Artikel:
link: / statistische-formeln-wie-man-die-t-test-funktion-in-excel benutzt [wie man die Excel-T-TEST-Funktion in Excel verwendet]: Der T.TEST wird verwendet, um das Vertrauen einer Analyse zu bestimmen. Mathematisch wird verwendet, um zu wissen, ob der Mittelwert der beiden Stichproben gleich ist oder nicht. T.TEST wird verwendet, um die Nullhypothese zu akzeptieren oder abzulehnen.
link: / statistische-formeln-wie-zu-verwenden-excel-f-test-funktion [Verwendung der Excel F.TEST-Funktion in Excel]: Die F.TEST-Funktion wird verwendet, um die F-Statistik von zwei Stichproben in zu berechnen Excel intern und gibt die zweiseitige Wahrscheinlichkeit der F-Statistik unter Nullhypothese zurück.
link: / statistische-formeln-wie-man-die-devsq-funktion-in-excel benutzt [wie man die DEVSQ-Funktion in Excel benutzt]: Die DEVSQ-Funktion ist eine eingebaute statistische Funktion zur Berechnung der Quadratsumme Abweichungen vom Mittelwert oder Durchschnitt des Bereichs der bereitgestellten Datenwerte.
link: / static-formulas-how-to-use-excel-normdist-function [Verwendung der Excel-NORM.DIST-Funktion]: Berechnen Sie den Z-Score für die normale kumulative Verteilung für die vorgegebenen Werte mit der NORMDIST-Funktion in Excel.
link: / statistische-formeln-wie-man-die-excel-norm-inv-funktion benutzt [wie man die Excel NORM.INV-Funktion benutzt]: Berechnen Sie die Umkehrung des Z-Scores für die kumulative Normalverteilung für die vorgegebene Wahrscheinlichkeit Werte mit der Funktion NORM.INV in Excel.
link: / excel-finanzielle-formeln-wie-berechnet-standard-abweichung-in-excel [Berechnen der Standardabweichung in Excel]: * Um die Standardabweichung zu berechnen, haben wir verschiedene Funktionen in Excel. Die Standardabweichung ist die Quadratwurzel des Varianzwerts, sagt jedoch mehr über den Datensatz als über die Varianz aus.
link: / static-formulas-excel-var-function [Verwendung der VAR-Funktion in Excel]: Berechnen Sie die Varianz für den Beispieldatensatz in Excel mithilfe der VAR-Funktion in Excel.
Beliebte Artikel:
link: / tips-if-condition-in-excel [Verwendung der IF-Funktion in Excel]: Die IF-Anweisung in Excel überprüft die Bedingung und gibt einen bestimmten Wert zurück, wenn die Bedingung TRUE ist, oder gibt einen anderen bestimmten Wert zurück, wenn FALSE .
link: / formeln-und-funktionen-einführung-der-vlookup-funktion [Verwendung der VLOOKUP-Funktion in Excel]: Dies ist eine der am häufigsten verwendeten und beliebtesten Funktionen von Excel, die zum Nachschlagen von Werten aus verschiedenen Bereichen verwendet wird und Blätter. link: / excel-formel-und-funktion-excel-sumif-funktion [Verwendung der SUMIF-Funktion in Excel]: Dies ist eine weitere wichtige Dashboard-Funktion. Auf diese Weise können Sie Werte unter bestimmten Bedingungen zusammenfassen.
link: / tips-countif-in-microsoft-excel [Verwendung der COUNTIF-Funktion in Excel]: Zählen Sie Werte mit Bedingungen, die diese erstaunliche Funktion verwenden. Sie müssen Ihre Daten nicht filtern, um bestimmte Werte zu zählen. Die Countif-Funktion ist wichtig, um Ihr Dashboard vorzubereiten.