¿Cómo encontrar coeficiente de correlación en Excel
¿Cuál es el coeficiente de correlación?
El coeficiente de correlación de un conjunto de datos es un número estadístico que indica qué tan fuertemente están relacionadas dos variables entre sí. Se puede decir que es el porcentaje de la relación entre dos variables (xey). No puede ser mayor al 100% ni menor al -100%.
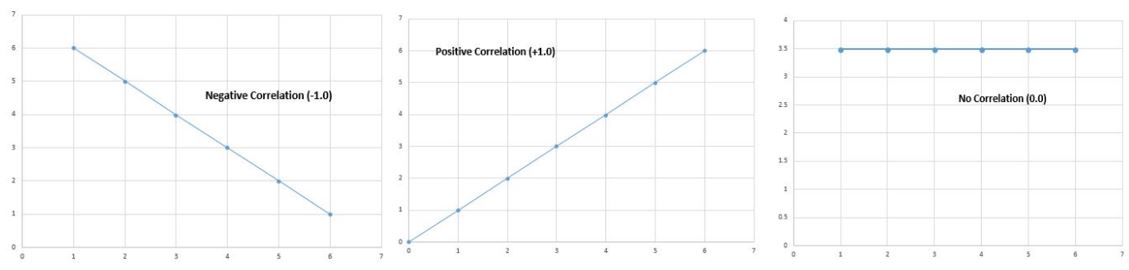
El coeficiente de correlación se sitúa entre -1,0 y +1,0.
Un coeficiente de correlación negativo nos dice que si una variable aumenta, la otra disminuye. Una correlación de -1,0 es una correlación negativa perfecta. Esto significa que si x aumenta en 1 unidad, y disminuye en 1 unidad.
Un coeficiente de correlación positivo nos dice que si el valor de una variable aumenta, el valor de otra también aumenta. Esto significa que si x aumenta en 1 unidad, y también aumenta en 1 unidad.
La correlación de 0 dice que no existe relación entre dos variables.
La fórmula matemática del coeficiente de correlación es:
Cobertura ~ xy ~ / (Estándar ~ x ~ * Estándar ~ y ~)
La cobertura ~ xy ~ es la covarianza (muestra o población) del conjunto de datos.
Std ~ x ~ = Es la desviación estándar (muestra o población) de Xs.
Std ~ y = ~ Es la desviación estándar (muestra o población) de Ys.
¿Cómo calcular el coeficiente de correlación en Excel?
Si necesita calcular la correlación en Excel, no es necesario que utilice la fórmula matemática. Puede utilizar estos métodos. Cálculo del coeficiente de correlación mediante la función COREL.
-
Cálculo del coeficiente de correlación utilizando Analysis Toolpak.
Veamos un ejemplo para saber cómo calcular el coeficiente de correlación en Excel.
Ejemplo de cálculo del coeficiente de correlación en Excel Aquí tengo un conjunto de datos de muestra. Tenemos xs en el rango A2: A7 e ys en B2: B7.
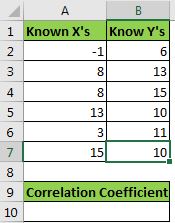
Necesitamos calcular el coeficiente de correlación de xs e ys.
Usando la función CORREL de Excel
Sintaxis de la función CORREL:
|
=CORREL(array1,array2) |
array1: * Este es el primer conjunto de valores (xs)
array2: * Es el segundo conjunto de valores (ys).
Nota: la matriz 1 y la matriz 2 deben ser del mismo tamaño.
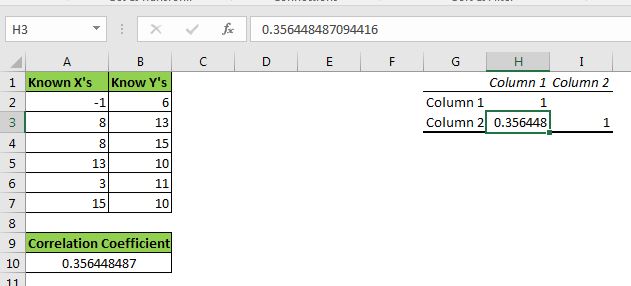
Usemos la función CORREL para obtener el coeficiente de correlación. Escribe esta fórmula en A10.
|
=CORREL(A2:A7,B2:B7) |
Obtenemos una correlación de 0.356448487 o 36% entre xey.
Usando el paquete de herramientas de análisis de Excel
Para calcular la correlación utilizando el paquete de herramientas de análisis, siga estos pasos:
-
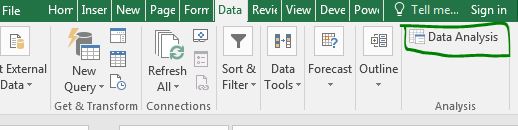
Vaya a la pestaña Datos en la cinta. En la esquina más a la izquierda, encontrará la opción de análisis de datos. Haz click en eso. Si no puede verlo, primero necesita
link: / tips-the-analysis-toolpak-in-excel [instalar el paquete de herramientas de análisis].
-
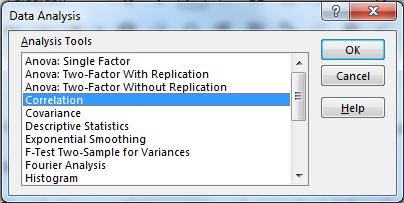
De las opciones disponibles, seleccione Correlación.
-
Seleccione el rango de entrada como A2: B7. Seleccione el rango de salida donde desea ver su salida.
-
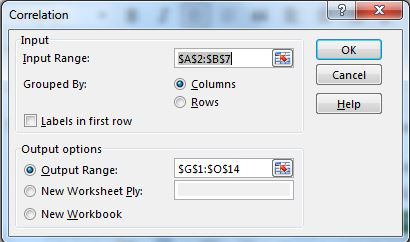
Pulsa el botón Aceptar. Tiene su coeficiente de correlación en el rango deseado. Es exactamente el mismo valor que devuelve la función CORREL.
How correlation is being calculated?* To understand how we are getting this value, we need to find it manually. This will clear our doubts.
Como sabemos, el coeficiente de correlación es:
Cobertura ~ xy ~ / (Estándar ~ x ~ * Estándar ~ y ~)
Primero, necesitamos calcular la covarianza. Podemos usar la función COVERIACE.S de Excel para calcularlo.
|
=COVARIANCE.S(A2:A7,B2:B7) |
A continuación, calculemos la desviación estándar de xey usando el`link: / stats-formulas-how-to-use-stdev-s-function-in-excel [STDEV.S] `
función.
|
= |
|
= |
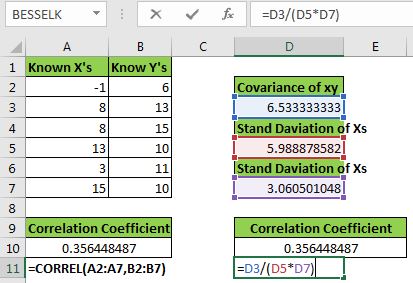
Ahora en la celda D10, escribe esta fórmula.
|
=D3/(D5*D7) |
Esto es equivalente a = Covarianza ~ xy ~ / (Std ~ x ~ * Std ~ y ~). Puede ver que obtenemos exactamente el mismo valor dado por la función CORREL. Ahora ya sabe cómo hemos obtenido el coeficiente de correlación en Excel.
Nota: * En el ejemplo anterior, hemos utilizado COVARIANCE.S (covarianza de la muestra) y `link: / statistics-formulas-how-to-use-stdev-s-function-in-excel [STDEV.S] `
(desviación estándar de la muestra). El coeficiente de correlación será el mismo si usa COVARIANCE.P y`link: / statistics-formulas-how-to-use-excel-stdev-p-function [STDEV.P] . Siempre que ambos sean de la misma categoría, no habrá diferencia. Si usa COVARIANCE.S (covarianza de la muestra) y `enlace: / fórmulas-estadísticas-cómo-usar-excel-stdev-p-function [DESVEST.P]
(desviación estándar de la población), entonces el resultado será diferente e incorrecto .__ Así que sí, chicos, así es como podemos calcular el coeficiente de correlación en Excel. Espero que esto sea lo suficientemente explicativo para explicar el coeficiente de correlación. Ahora puede crear su propia calculadora de coeficientes de correlación en Excel.
Artículos relacionados:
enlace: / fórmulas-estadísticas-calcular-interceptar-en-excel [Calcular INTERCEPTO en Excel]
vínculo: / fórmulas-estadísticas-cálculo-pendiente-en-excel [Cálculo de PENDIENTE en Excel]
enlace: / tips-regression-data-analysis-tool [Regresiones en Excel]
enlace: / fórmulas-estadísticas-cómo-crear-gráfico-de-desviación-estándar-en-excel [Cómo crear un gráfico de desviación estándar]
link: / tips-descriptive-statistics [Estadísticas descriptivas en Microsoft Excel 2016]
enlace: / fórmulas-estadísticas-cómo-usar-excel-normdist-function [Cómo usar la función NORMDIST de Excel]
link: / tips-how-to-create-a-Pareto-chart-in-microsoft-excel [Pareto Chart and Analysis]
Artículos populares:
link: / keyboard-formula-shortcuts-50-excel-shortcuts-to-incrementa-your-productividad [50 Excel Shortcut to Increase Your Productivity]
enlace: / fórmulas-y-funciones-introducción-de-vlookup-function [La función VLOOKUP en Excel]
enlace: / tips-countif-in-microsoft-excel [COUNTIF en Excel 2016]
link: / excel-formula-and-function-excel-sumif-function [Cómo usar la función SUMIF en Excel]