Cómo utilizar la función de Excel COVARIANCE.S?
¿Qué es la covarianza?
Como aprendimos en enlace: / fórmulas-estadísticas-cómo-usar-excel-covarianza-p [función COVERAINCE.P], la medición de la relación entre las dos variables aleatorias se llama covarianza. Como sugiere el nombre, la covarianza de las dos variables nos dice cómo varía una variable cuando cambia la otra. La covarianza no define la dependencia de una variable de otra. Hay dos tipos de cálculos de covarianza.
Primero es la covarianza de la población y el otro es la covarianza de la muestra. En este artículo, aprenderemos a calcular la covarianza de la muestra en Excel.
El valor de covarianza puede ser un valor negativo o positivo. Un valor negativo significa que ambas variables se mueven en direcciones opuestas. Y, lo adivinó bien, una covarianza positiva significa que las dos variables se mueven en la misma dirección.
Puede sonar como un enlace: / fórmulas-estadísticas-cómo-encontrar-coeficiente-de-correlación-en-excel [coeficiente de correlación] pero es diferente. Hablaremos de ello al final.
¿Cómo encontrar la covarianza de la muestra en Excel?
Excel proporciona COVARIANCE.S para calcular fácilmente la covarianza de datos de muestra. Se introdujo en Excel 2010 y, desde esa versión, se está utilizando ampliamente. Lo estoy usando en Excel 2016. Hay otra versión de este método llamada enlace: / fórmulas-estadísticas-cómo-usar-excel-covarianza-p [COVARIANCIA.P], que se usa para calcular la covarianza de la población.
La sintaxis de COVARIANCE.S:
|
=COVARIANCE.S(array1,array2) |
Array1: * Los valores de la primera variable.
Array2: * Los valores de la segunda variable.
Nota: * Estas matrices se pueden colocar en cualquier orden. La longitud de las dos matrices debe ser la misma. Si las dos matrices son de dos longitudes diferentes, Excel mostrará el error # N / A.
Ahora que conocemos la covarianza, veamos un ejemplo para aclarar aún más las cosas.
Ejemplo: Calcule la covarianza de la población en Excel
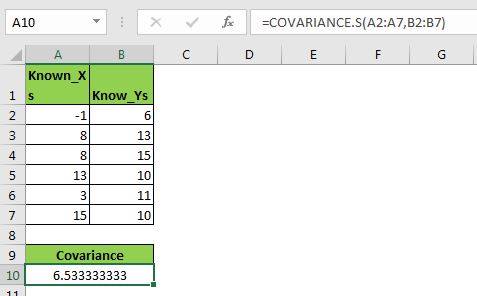
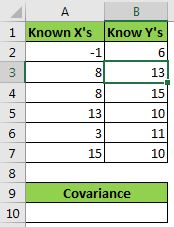
Aquí tengo un conjunto de datos de muestra. En el rango A2: A7, tengo una variable X y en el rango B2: B7 otra variable Y. Ahora calculemos las covarianzas de estos datos y veamos cómo estas dos variables se afectan entre sí.
 Let’s use the Excel COVARAINCE.S function:
Let’s use the Excel COVARAINCE.S function:
|
=COVARIANCE.S(A2:A7,B2:B7) |
Esto devuelve un valor de 6.533333333.
Interpretación de covarianza
El valor de covarianza que obtuvimos es un valor positivo. Dice que X e Y se mueven en la misma dirección. En otras palabras, Y aumentará si X aumenta y viceversa. Si la covarianza fuera un valor negativo, lo contrario sería cierto.
¿Cómo se calcula COVARIANCE.S?
Bueno, la fórmula matemática para calcular la covarianza de la muestra es la siguiente:
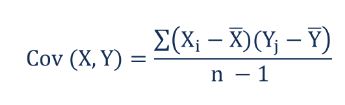
Aquí X ~ i ~ es cualquier valor en la variable X donde X bar es la media muestral de la variable X.
Y ~ i ~ es cualquier valor en la variable Y donde Y bar es la media muestral de la variable Y.
N es el numero de observaciones. Restamos 1 del denominador. Es por estar seguro, ya que son solo datos de muestra y hemos tomado nota de los datos capturados de toda la población. Por eso siempre es mayor que la covarianza de la población.
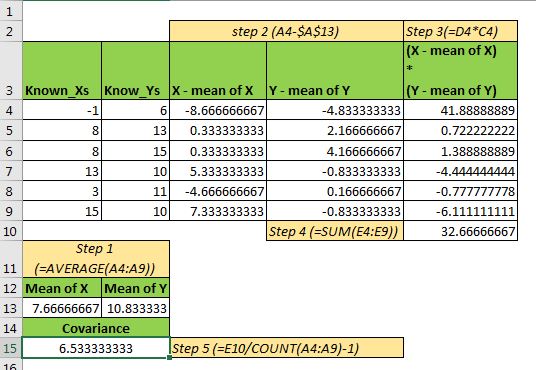
Si intenta calcular la covarianza de la muestra en Excel manualmente, así es como lo haría.
-
Primero,
enlace: / fórmulas-estadísticas-cómo-calcular-la-media-en-excel [calcular la media aritmética]de las variables X e Y en la celda. Puede utilizar la función PROMEDIO.
|
= |
-
Reste la media de X de cada valor de X. Haga lo mismo con Y.
|
=A4-$A$13 |
-
Ahora múltiples rangos de X-mean X e Y-mean Y. Vea la imagen de arriba.
|
=D4*C4 |
-
Ahora, suma los valores obtenidos mediante la multiplicación.
|
=SUM(E4:E9) |
-
Finalmente, divida la suma obtenida con una serie de observaciones. En nuestro caso, es 6.
|
=E10/( |
El número que obtenemos es 6.533333333, que es exactamente el mismo que obtuvimos de la función COVARIANCE.S de Excel.
La diferencia en covarianza y coeficiente de correlación
La primera y principal diferencia es la fórmula. El vínculo: / fórmulas-estadísticas-cómo-encontrar-coeficiente-de-correlación-en-excel [coeficiente de correlación] se calcula dividiendo la covarianza por el producto de la desviación estándar de Xs e Ys.
La covarianza nos dice la dirección de dos variables aleatorias, ya sea que se muevan en la misma dirección o en una dirección diferente. No dice la fuerza de la relación entre dos variables. Donde la correlación muestra la fuerza de la relación entre dos variables en el rango -100% a 100%.
Así que sí, chicos, así es como se usa COVARIANCE.P en Excel. En este artículo, no solo aprendimos sobre la función COVARIANCE.P, sino que también aprendimos cómo la calculamos manualmente y cómo la derivamos. Espero haber sido lo suficientemente explicativo. Si tiene alguna duda sobre esta función estática o cualquier otra función estática de Excel, coméntela en la sección de comentarios a continuación.
Artículos relacionados:
enlace: / fórmulas-estadísticas-cómo-encontrar-coeficiente-de-correlación-en-excel [Cómo encontrar el coeficiente de correlación en Excel]
enlace: / fórmulas-estadísticas-calcular-interceptar-en-excel [Calcular INTERCEPTO en Excel]
enlace: / fórmulas-estadísticas-calculando-pendiente-en-excel [Calculando PENDIENTE en Excel]
link: / stats-formulas-how-to-use-excel-normdist-function [Cómo usar la función NORMDIST de Excel]
enlace: / tips-regression-data-analysis-tool [Regresiones en Excel 2010]
link: / tips-how-to-create-a-Pareto-chart-in-microsoft-excel [Pareto Chart and Analysis]
Artículos populares:
link: / keyboard-formula-shortcuts-50-excel-shortcuts-to-incrementa-your-productividad [50 Excel Shortcut to Increase Your Productivity]
enlace: / fórmulas-y-funciones-introducción-de-vlookup-function [La función VLOOKUP en Excel]
enlace: / tips-countif-in-microsoft-excel [COUNTIF en Excel 2016]
link: / excel-formula-and-function-excel-sumif-function [Cómo usar la función SUMIF en Excel]