Cómo utilizar la función Z.TEST en Excel
En este artículo, aprenderemos cómo usar la función Z.TEST en Excel.
¿Qué es la prueba de hipótesis y cómo utilizar Z -Test para la prueba de hipótesis? En estadística, la prueba de hipótesis se utiliza para encontrar la estimación de la media para el conjunto de datos de población utilizando la función de distribución diferente basada en la parte del conjunto de datos de población denominada conjunto de datos de muestra. Una hipótesis estadística, a veces llamada análisis de datos confirmatorios, es una hipótesis que se puede comprobar sobre la base de la observación de un proceso que se modela mediante un conjunto de variables aleatorias. Hay dos tipos de hipótesis. Una es la hipótesis nula, que es la declaración reclamada y la otra es la hipótesis alternativa, que es exactamente opuesta a la hipótesis nula. Por ejemplo, si decimos que el límite máximo de plomo en un paquete maggi no debe exceder de 225 ppm (partes por millón) y alguien afirma que hay más de un límite fijo que la hipótesis nula (indicada por U ~ 0 ~) y la hipótesis alternativa (indicada por U ~ a ~)
U ~ 0 ~ = el contenido de plomo en el paquete maggi es mayor o igual a 225 ppm. U ~ a ~ = el contenido de plomo en el paquete maggi es inferior a 225 ppm.
Entonces, la hipótesis anterior es un ejemplo de una prueba de cola derecha, ya que la situación subyacente se encuentra en el lado derecho de la curva de distribución.
Si la situación subyacente se encuentra en el lado izquierdo, se llamaría prueba de cola izquierda. Tomemos un ejemplo más que ilustra una prueba de una cola. Por ejemplo, si Selina dijo que puede hacer 60 flexiones en promedio. Ahora puede dudar de esa afirmación y tratar de hacer una hipótesis de la situación en términos estadísticos, entonces, la hipótesis nula y alternativa se establece a continuación U ~ 0 ~ = selina puede hacer 60 flexiones U ~ a ~ = selina no puede hacer 60 flexiones Esta es una -prueba detallada donde la situación subyacente se encuentra a ambos lados de la declaración reclamada Estas pruebas de cola afectan el resultado de las estadísticas. Por lo tanto, elija cuidadosamente la hipótesis nula y alternativa.
Prueba Z Una prueba Z es cualquier prueba estadística para la cual la distribución de la estadística de prueba bajo la hipótesis nula se puede aproximar mediante una distribución normal. La prueba Z prueba la media de una distribución en la que ya conocemos la varianza de la población. Debido al teorema del límite central, muchos estadísticos de prueba tienen una distribución aproximadamente normal para muestras grandes. Se asume que la estadística de prueba tiene una distribución normal, como la desviación estándar debe conocerse para poder realizar una prueba z precisa. Por ejemplo, un inversor desea probar si el rendimiento medio diario de una acción es superior al 1% y puede evaluarse mediante la prueba Z. Una estadística Z o puntuación Z * es un número que representa cuántas desviaciones estándar por encima o por debajo de la población media tiene una puntuación derivada de una prueba Z. Primero decidimos matemáticamente la hipótesis nula y calculamos la puntuación Z para la distribución usando la fórmula.
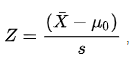
Aquí X (con una barra) es la media de la matriz de muestra U ~ 0 ~ es la media de la población estimada s es la desviación estándar donde s es igual a std / (n) ^ 1/2 ^ (donde n es el tamaño de la muestra) .
Como se indicó anteriormente, la prueba Z sigue una distribución normal estándar. Entonces matemáticamente en Excel sigue la siguiente fórmula.
PRUEBA Z (matriz, x, sigma) = 1- Lista normal. S. ((Promedio (matriz) – x) / (sigma / (n) ^ 1/2 ^), VERDADERO)
o cuando se omite sigma:
PRUEBA Z (matriz, x) = 1- Lista estándar. S. ((Promedio (matriz) – x) / (DESVEST (matriz) / (n) ^ 1/2 ^), VERDADERO)
donde x es la media de la muestra PROMEDIO (matriz) yn es CONTAR (matriz).
Aprendamos a hacer la prueba Z usando la función Z.TEST para calcular la relación entre los dos conjuntos de datos dados (real y observado).
Función Z.TEST en Excel
La función PRUEBA Z devuelve la probabilidad de que la media de la muestra sea mayor que el promedio de observaciones en el conjunto de datos (matriz). La función toma los siguientes argumentos.
Z.TEST Sintaxis de la función para probabilidad de una cola:
|
=Z.TEST ( array , x , [sigma] ) |
La función también se puede utilizar para conmutar la probabilidad de dos colas.
Z.TEST Sintaxis de la función para probabilidad de una cola:
|
=2 * MIN(Z.TEST ( array , x , [sigma] ), 1-Z.TEST ( array , x , [sigma] ) ) |
matriz: distribución de datos de muestra x: valor para el que se evalúa la prueba z [sigma] *: [opcional] La desviación estándar de la población (conocida). Si se omite, se utiliza la desviación estándar de la muestra.
Ejemplo:
Todos estos pueden ser confusos de entender. Entendamos cómo usar la función usando un ejemplo. Aquí tenemos un conjunto de datos de muestra Ventas y necesitamos encontrar la probabilidad de la prueba Z para la media poblacional hipotética dada asumiendo una prueba de una cola.
Usa la fórmula:
|
= Z.TEST( A2:A9 , C3 ) |
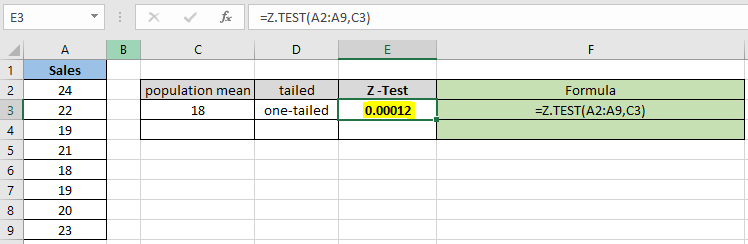
El valor de probabilidad viene en decimal, por lo que puede convertir el valor a porcentaje cambiando el formato de la celda a porcentaje.
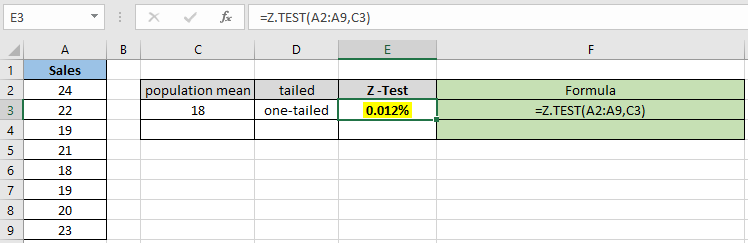
Como puede ver, el valor de probabilidad para la media poblacional hipotética 18 resulta ser 0.012% para la distribución de una cola. Ahora calcule la probabilidad asumiendo dos distribuciones con colas que tienen los mismos parámetros.
Usa la fórmula:
|
= 2 * MIN( Z.TEST(A2:A9,C4) , 1 – Z.TEST(A2:A9,C4) ) |
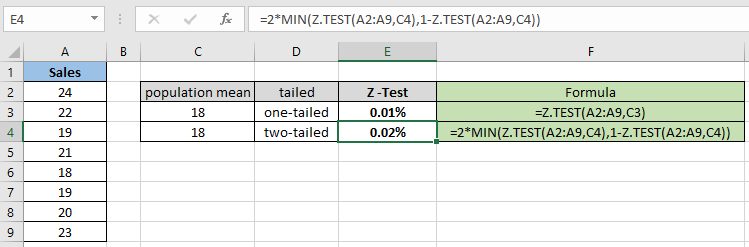
Para la distribución de dos colas, la probabilidad se duplica para el mismo conjunto de datos de muestra. Entonces es necesario verificar la hipótesis nula y la hipótesis alternativa. Ahora calcule la probabilidad para las diferentes medias poblacionales hipotetizadas y una distribución de cola.
Usa la fórmula:
|
= Z.TEST( A2:A9 , C5 ) |
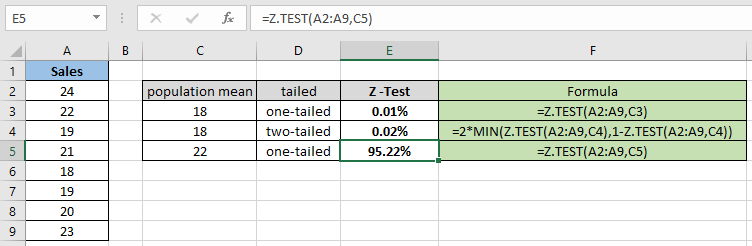
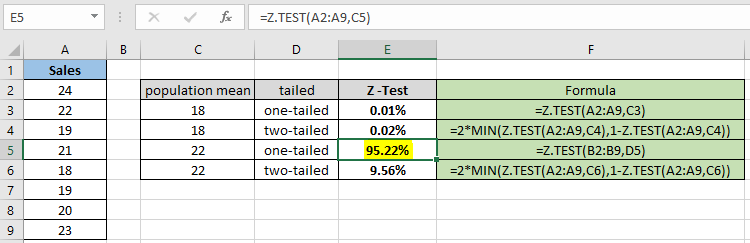
Como puede ver, el valor de probabilidad para la media poblacional hipotética 22 resulta ser 95.22% para la distribución de una cola. Ahora calcule la probabilidad asumiendo dos distribuciones con colas que tienen los mismos parámetros.
Usa la fórmula:
|
= 2 * MIN( Z.TEST(A2:A9,C6) , 1 – Z.TEST(A2:A9,C6) ) |
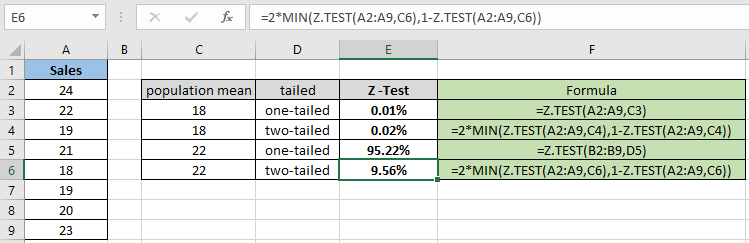
Como puede diferir de la instantánea anterior, el valor de probabilidad es menor cuando se calcula la distribución de dos colas. La función devuelve 9.56% para la media poblacional hipotética 22.
PRUEBA Z representa la probabilidad de que la media de la muestra sea mayor que el valor observado PROMEDIO (matriz), cuando la media de la población subyacente es 0. De la simetría de la distribución Normal, si PROMEDIO (matriz) <x, PRUEBA Z devuelve un valor superior a 0,5.
Aquí están todas las notas de observación usando la función Z.TEST en Excel
Notas:
-
La función solo funciona con números. Si la media de población o el argumento sigma no es numérico, la función devuelve # ¡VALOR! error.
-
El valor en decimal o el valor en porcentaje es el mismo valor en Excel.
Convierta el valor a porcentaje, si es necesario.
-
La función devuelve # ¡NUM! Error, si el argumento sigma es 0.
-
¡La función devuelve # N / A! Error si la matriz proporcionada está vacía.
-
¡La función devuelve # DIV / 0! Error, .. Si la desviación estándar de la matriz es 0 y se omite el argumento sigma.
-
Si la matriz contiene solo un valor.
-
Espero que este artículo sobre cómo usar la función Z.TEST en Excel sea explicativo. Encuentre más artículos sobre fórmulas estadísticas y funciones de Excel relacionadas aquí. Si te gustaron nuestros blogs, compártelo con tus amigos en Facebook. Y también puedes seguirnos en Twitter y Facebook. Nos encantaría saber de usted, háganos saber cómo podemos mejorar, complementar o innovar nuestro trabajo y hacerlo mejor para usted. Escríbanos a [email protected].
Artículos relacionados:
link: / statistics-formulas-how-to-use-t-test-function-in-excel [Cómo usar la función TEST de Excel en Excel]: El T.TEST se utiliza para determinar la confianza de un análisis. Matemáticamente, se utiliza para saber si la media de las dos muestras es igual o no. T.TEST se utiliza para aceptar o rechazar la hipótesis nula.
link: / statistics-formulas-how-to-use-excel-f-test-function [Cómo usar la función F.TEST de Excel en Excel]: La función F.TEST se usa para calcular el estadístico F de dos muestras en sobresale internamente y devuelve la probabilidad de dos colas del estadístico F bajo Hipótesis nula.
enlace: / fórmulas-estadísticas-cómo-usar-la-función-devsq-en-excel [Cómo usar la función DEVSQ en Excel]: La función DEVSQ es una función estadística incorporada para calcular la suma de cuadrados desviaciones de la media o promedio del rango de valores de datos proporcionados.
link: / statistics-formulas-how-to-use-excel-normdist-function [Cómo usar la función NORM.DIST de Excel]: Calcule el puntaje Z para la distribución acumulativa normal para los valores preespecificados usando la función NORMDIST en Sobresalir.
link: / statistics-formulas-how-to-use-excel-norm-inv-function [Cómo usar la función Excel NORM.INV]: Calcule la inversa de la puntuación Z para la distribución acumulativa normal para la probabilidad preespecificada valores usando la función NORM.INV en Excel.
link: / excel-financial-formulas-how-to-calculate-standard-desviation-in-excel [Cómo calcular la desviación estándar en Excel]: * Para calcular la desviación estándar tenemos diferentes funciones en Excel. La desviación estándar es la raíz cuadrada del valor de la varianza, pero dice más sobre el conjunto de datos que la varianza.
link: / statistics-formulas-excel-var-function [Cómo usar la función VAR en Excel]: Calcule la varianza para el conjunto de datos de muestra en Excel usando la función VAR en Excel.
Artículos populares:
link: / tips-if-condition-in-excel [Cómo usar la función IF en Excel]: La declaración IF en Excel verifica la condición y devuelve un valor específico si la condición es VERDADERA o devuelve otro valor específico si es FALSO .
link: / formulas-and-functions-introduction-of-vlookup-function [Cómo usar la función VLOOKUP en Excel]: Esta es una de las funciones más utilizadas y populares de Excel que se usa para buscar valores de diferentes rangos y sábanas. link: / excel-formula-and-function-excel-sumif-function [Cómo usar la función SUMIF en Excel]: Esta es otra función esencial del tablero. Esto le ayuda a resumir valores en condiciones específicas.
link: / tips-countif-in-microsoft-excel [Cómo usar la función CONTAR.SI en Excel]: Cuente valores con condiciones usando esta función asombrosa. No necesita filtrar sus datos para contar valores específicos. La función Countif es esencial para preparar su tablero.