esempio IRR Semplice | valori attuali | regola IRR

Utilizzare la funzione IRR in Excel per calcolare tasso interno di un progetto di rendimento. Il tasso di rendimento interno è il tasso di sconto che rende il valore attuale netto pari a zero.

esempio IRR semplice

Ad esempio, il progetto A richiede un investimento iniziale di $ 100 (cella B5).

  1. ci aspettiamo un profitto di $ 0 alla fine del primo periodo, un profitto di $ 0 alla fine del secondo periodo e un profitto di $ 152.09 alla fine del terzo periodo.

Cash Flows

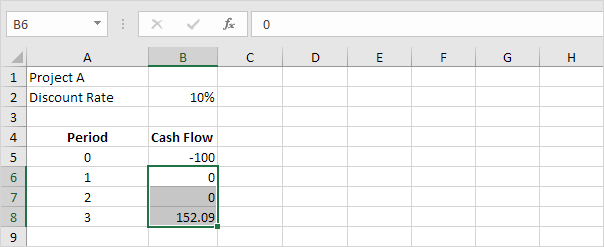
Nota: il tasso di sconto pari al 10%. Questo è il tasso di rendimento del migliore investimento alternativo. Ad esempio, si potrebbe anche mettere il proprio denaro in un conto di risparmio a un tasso di interesse del 10%.

  1. Il link corretto : / examples-VAN [formula NPV] in Excel utilizza la funzione NPV per calcolare il valore attuale di una serie di flussi di cassa futuri e sottrae l’investimento iniziale.

Net Present Value

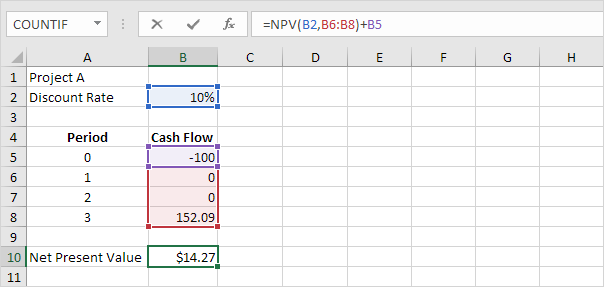
Spiegazione: un valore attuale netto positivo indica che il tasso del progetto di rendimento superiore al tasso di sconto. In altre parole, è meglio investire i vostri soldi nel progetto A che mettere il vostro denaro in un conto di risparmio a un tasso di interesse del 10%.

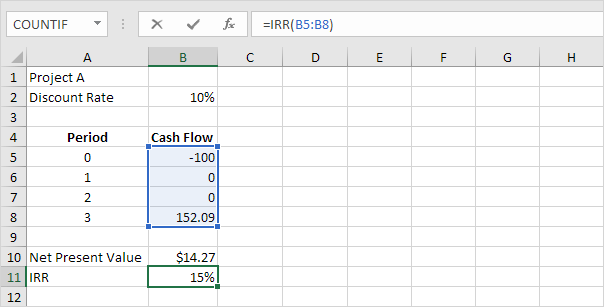
  1. La funzione IRR sottostante calcola il tasso di rendimento interno del progetto A.

IRR function in Excel

  1. Il tasso di rendimento interno è il tasso di sconto che rende il valore attuale netto pari a zero. Per vedere chiaramente questo, sostituire il tasso di sconto del 10% nella cella B2 con il 15%.

Net Present Value of 0

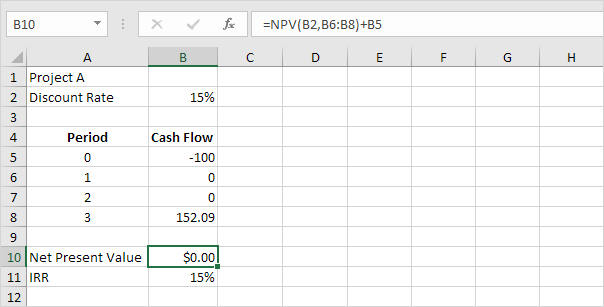
Spiegazione: un valore attuale netto di 0 indica che il progetto genera un tasso di rendimento pari al tasso di sconto. In altre parole, entrambe le opzioni, investire il vostro denaro nel progetto A o di mettere il vostro denaro in un alto rendimento conto di risparmio ad un tasso di interesse del 15%, producono un rendimento uguale.

  1. Possiamo controllare questo. Si supponga di mettere $ 100 in una banca. Quanto sarà il vostro investimento vale la pena dopo 3 anni ad un tasso di interesse annuo del 15%? La risposta è di $ 152.09.

Compound Interest

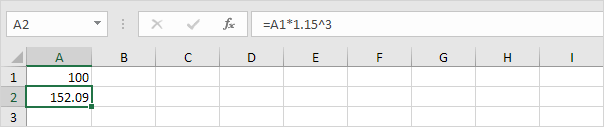
Conclusione: è possibile confrontare le prestazioni di un progetto per un conto di risparmio con un tasso di interesse pari al IRR.

valori attuali

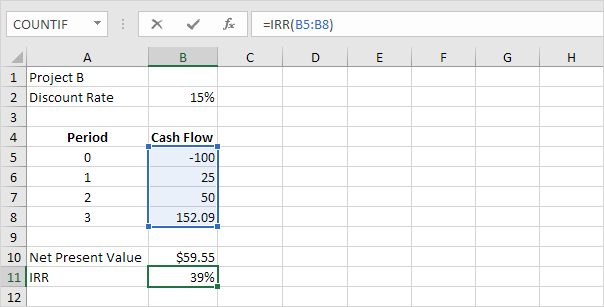
Ad esempio, il progetto B richiede un investimento iniziale di $ 100 (cella B5).

Ci aspettiamo un profitto di $ 25 alla fine del primo periodo, un profitto di $ 50 alla fine del secondo periodo e un profitto di $ 152.09 alla fine del terzo periodo.

  1. La funzione IRR sottostante calcola il tasso di rendimento interno del progetto B.

Internal Rate of Return

  1. Anche in questo caso, il tasso di rendimento interno è il tasso di sconto che rende il valore attuale netto pari a zero. Per vedere chiaramente questo, sostituire il tasso di sconto del 15% nella cella B2 con il 39%.

NPV equals 0

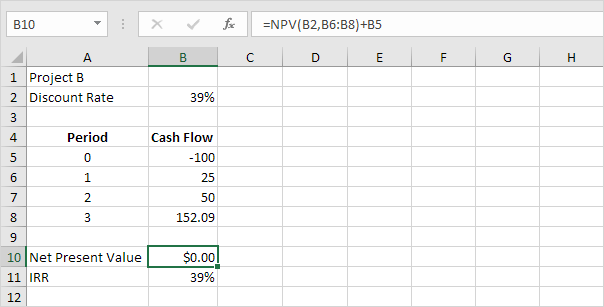
Spiegazione: un valore attuale netto di 0 indica che il progetto genera un tasso di rendimento pari al tasso di sconto. In altre parole, entrambe le opzioni, investire il vostro denaro in progetto di B o di mettere il vostro denaro in un alto rendimento conto di risparmio ad un tasso di interesse del 39%, producono un rendimento uguale.

  1. Possiamo controllare questo. In primo luogo, si calcola il valore attuale (PV) di ciascun flusso di cassa. Successivamente, abbiamo riassumere questi valori.

Sum Present Values

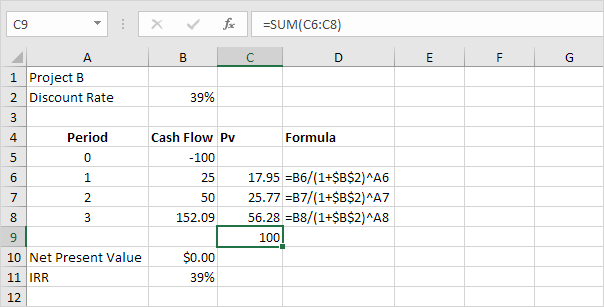
Spiegazione: invece di investire $ 100 nel progetto B, si potrebbe anche mettere $ 17.95 in un conto di risparmio per 1 anno, $ 25.77 in un conto di risparmio per 2 anni e $ 56.28 in un conto di risparmio per tre anni, a un tasso di interesse annuo pari alla IRR (39%).

regola IRR

La regola IRR afferma che se il TIR è maggiore del tasso di rendimento richiesto, si dovrebbe accettare il progetto. I valori IRR sono spesso utilizzati per confrontare gli investimenti.

  1. La funzione IRR sottostante calcola il tasso di rendimento interno del progetto X.

IRR

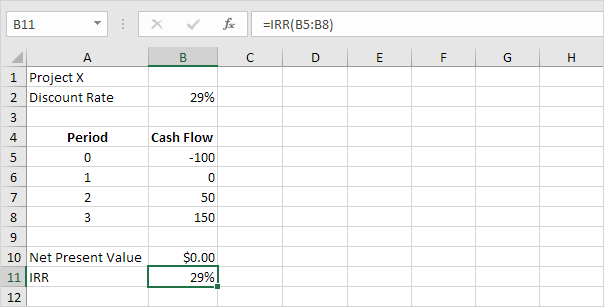
Conclusione: se il tasso di rendimento richiesto è pari al 15%, si dovrebbe accettare questo progetto perché il TIR di questo progetto è pari a 29%.

  1. La funzione IRR sottostante calcola il tasso di rendimento interno del progetto Y.

Higher IRR

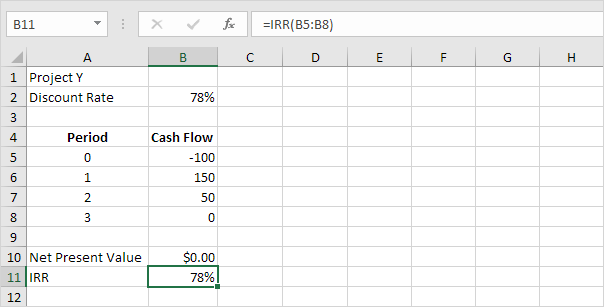
Conclusione: in generale, un IRR più alto indica un investimento migliore.

Pertanto, il progetto Y è un investimento migliore di progetto X.

  1. La funzione IRR sottostante calcola il tasso di rendimento interno del progetto Z.

Low Cash Flows

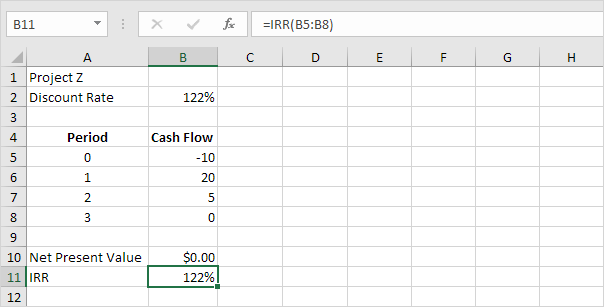
Conclusione: un IRR superiore non è sempre meglio. Progetto Z ha un IRR superiore al progetto Y, ma i flussi di cassa sono molto più bassi.