L’analisi di regressione in Excel
Questo esempio vi insegna come eseguire un’analisi di regressione lineare in Excel e come interpretare l’output di riepilogo.
Qui di seguito potete trovare i nostri dati. La grande domanda è: esiste una relazione tra quantità vendute (in uscita) e del prezzo e pubblicità (Input). In altre parole: possiamo prevedere Quantità venduta se conosciamo il prezzo e la pubblicità?
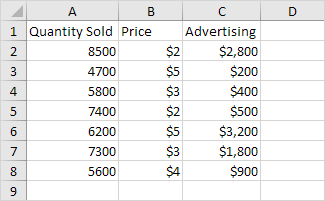
-
Nella scheda Dati, nel gruppo Analisi, scegliere Analisi dati.
Nota: non riesce a trovare il pulsante di analisi dei dati? Clicca qui per caricare gli strumenti di analisi aggiuntivo.
-
Selezionare regressione e fare clic su OK.
-
Selezionare la Y Range (A1: A8). Questa è la variabile predittore (chiamato anche variabile dipendente).
-
Selezionare l’intervallo X (B1: C8). Queste sono le variabili esplicative (chiamati anche variabili indipendenti). Queste colonne devono essere adiacenti l’uno all’altro.
-
Controllare le etichette.
-
Fare clic nella casella Intervallo di output e selezionare la cella A11.
-
Controllare Residui.
-
Fare clic su OK.
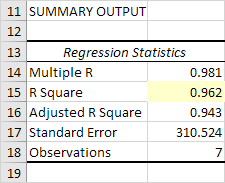
Excel produce il seguente output Summary (arrotondato a 3 decimale).
R Piazza
R al quadrato è uguale a 0,962, che è una misura molto buona. 96% della variazione della quantità venduta è spiegata dalle variabili prezzo indipendente e pubblicità. Il più vicino a 1, migliore è la retta di regressione (continua a leggere) si adatta ai dati.
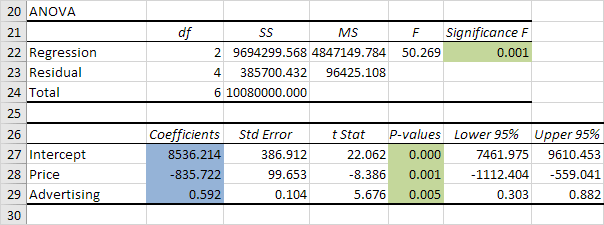
Significato F e P-valori
Per verificare se i risultati sono affidabili (statisticamente significativo), sguardo al significato F (0,001). Se questo valore è inferiore a 0,05, sei ok.
Se significato F è maggiore di 0,05, è probabilmente meglio a smettere di usare questo insieme di variabili indipendenti. Eliminare una variabile con un alto valore di P (maggiore di 0,05) e rieseguire la regressione fino Importanza F scende sotto 0,05.
La maggior parte o tutti i valori di P dovrebbe essere al di sotto di sotto di 0,05. Nel nostro esempio, questo è il caso. (0.000, 0.001 e 0.005).
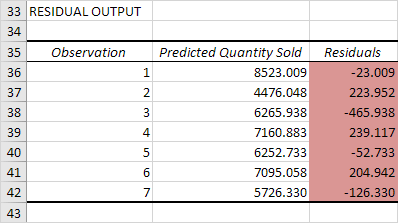
Coefficienti
La retta di regressione è: y = Quantità venduta = 8536,214 -835,722 Prezzo + 0,592 Pubblicità. In altre parole, per ogni unità di aumento di prezzo, Quantità venduta diminuisce con 835.722 unità. Per ogni unità di aumento Pubblicità, quantità aumenta venduto con 0.592 unità. Si tratta di informazioni preziose.
È inoltre possibile utilizzare questi coefficienti per fare una previsione. Ad esempio, se il prezzo è uguale a $ 4 e pubblicità pari a $ 3000, si potrebbe essere in grado di raggiungere un quantitativo venduto di 8536,214 -835,722 4 + 0,592 3000 = 6970.
Residui
I residui mostrano quanto lontano i punti dati reali sono fom i previsti punti di dati (utilizzando l’equazione). Ad esempio, il primo punto di dati è uguale 8500. Usando l’equazione, il punto dati predetto uguale 8536,214 -835,722 2 + 0,592 2800 = 8523,009, dando un residuo 8500 – 8523,009 = -23,009.
È inoltre possibile creare un grafico a dispersione di questi residui.