Formulare il Modello | Trial and Error | Collegamento: # risolvono-modello [Risolvere il Modello]

Utilizzare il risolutore in Excel per trovare il percorso più breve dal nodo al nodo S T in una rete non orientato. Punti in una rete sono detti nodi (S, A, B, C, D, E e T). Le linee in una rete sono chiamati archi (SA, SB, SC, AC, ecc).

Formulare il modello

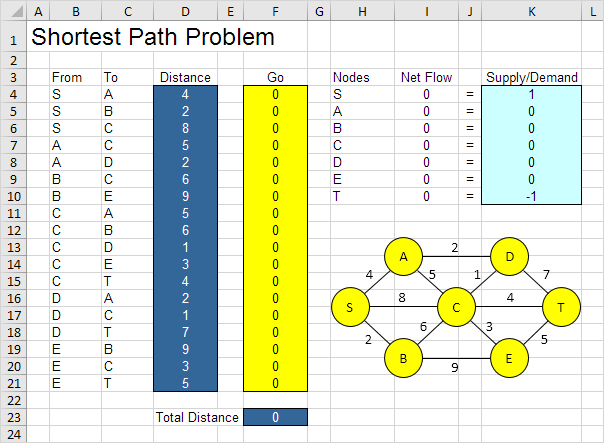
Il modello ci accingiamo a risolvere appare come segue in Excel.

Shortest Path Problem in Excel

  1. Per formulare questo problema del cammino minimo, rispondere alle seguenti tre domande.

\un. Quali sono le decisioni da prendere? Per questo problema, abbiamo bisogno di Excel per scoprire se un arco è il percorso più breve o no (sì = 1, No = 0). Per esempio, se SB è parte del percorso più breve, cellule F5 è uguale a 1. In caso contrario, la cella F5 è uguale a 0.

\ B. Quali sono i vincoli su queste decisioni? Il flusso netto (Flow Out – Flusso In) di ogni nodo deve essere uguale alla domanda / offerta. Nodo S dovrebbe avere un solo arco uscente (flusso netto = 1). Nodo T dovrebbe avere un solo arco in entrata (flusso netto = -1). Tutti gli altri nodi dovrebbero avere un arco in uscita e un arco in entrata se il nodo è il percorso più breve (flusso netto = 0) o assenza di flusso (flusso netto = 0).

\ C. Qual è la misura complessiva della prestazione per queste decisioni? La valutazione generale della performance è la distanza totale del percorso più breve, quindi l’obiettivo è quello di minimizzare questa quantità.

  1. Per rendere il modello più facile da capire, nominare i seguenti intervalli.

Range Name

Cells

From

B4:B21

To

C4:C21

Distance

D4:D21

Go

F4:F21

NetFlow

I4:I10

SupplyDemand

K4:K10

TotalDistance

F23

  1. Inserire le seguenti funzioni.

Insert Functions

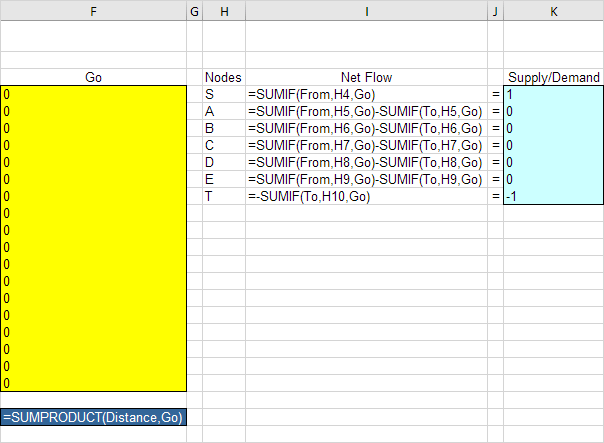
Spiegazione: Il link: / Esempi-SUMIF [SUMIF] funzioni calcolare il flusso netto di ogni nodo. Per il nodo S, la funzione SUMIF somma i valori nella colonna Go con una “S” nella colonna Da. Come risultato, solo cella F4, F5 ed F6 può essere 1 (un solo arco uscente). Per il nodo T, la funzione SUMIF somma i valori nella colonna Go con una “T” nella colonna To. Come risultato, solo F15 celle, F18 o F21 può essere 1 (un arco in entrata). Per tutti gli altri nodi, Excel guarda in Da e colonna. Distanza totale è uguale alla MATR.SOMMA.PRODOTTO di distanza e Go.

Trial and Error

Con questa formulazione, diventa facile per analizzare qualsiasi soluzione di prova.

  1. Ad esempio, lo SBET percorso ha una distanza totale di 16.

Trial Solution

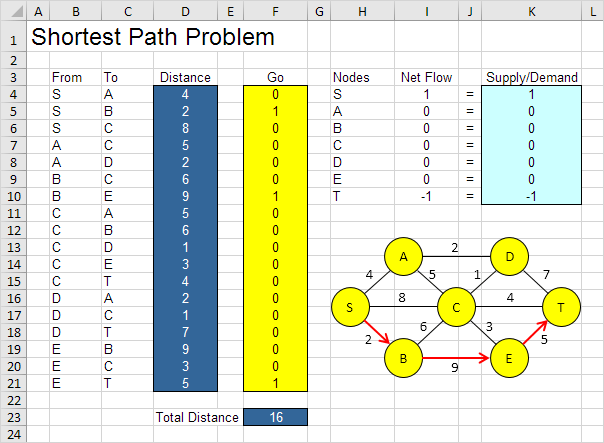
Non è necessario al processo uso ed errori. Descriveremo il prossimo come il Risolutore di Excel può essere utilizzato per trovare rapidamente la soluzione ottimale.

risolvere il modello

Per trovare la soluzione ottimale, eseguire le seguenti operazioni.

  1. Nella scheda Dati, nel gruppo Analizza, fare clic su Risolutore.

Click Solver

Nota: non riesce a trovare il pulsante Solver? Clicca qui per caricare il componente aggiuntivo Risolutore.

Inserire i parametri Solver (continua a leggere). Il risultato deve essere coerente con l’immagine qui sotto.

Solver Parameters

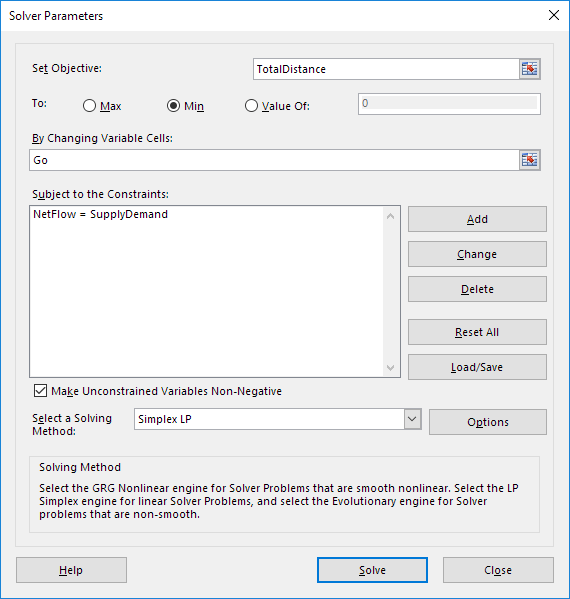
Avete la scelta di scrivere i nomi di intervallo o cliccando sulle celle del foglio di calcolo.

  1. Inserire TotalDistance per l’obiettivo.

  2. Fare clic su Min.

  3. Inserire Go per il cambio celle variabili.

  4. Fare clic su Aggiungi per immettere il seguente vincolo.

Net Flow Constraint

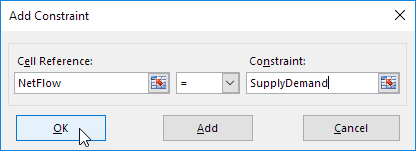
  1. Controllare ‘Fare Variabili non vincolata non negativi’ e selezionare ‘Simplex LP’.

  2. Infine, fare clic su Risolvi.

Risultato:

Solver Results

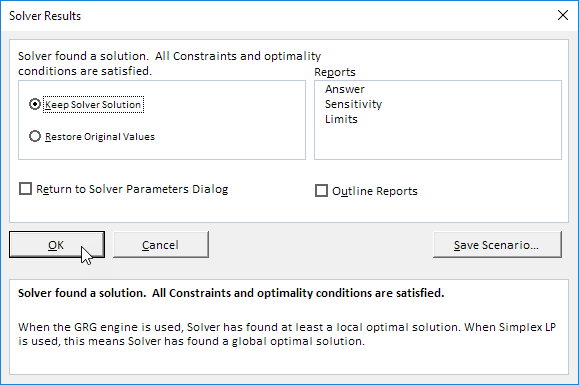
La soluzione ottimale:

Shortest Path Problem Result

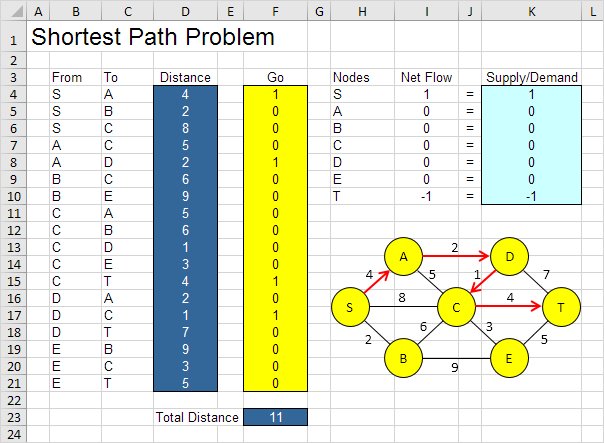
Conclusione: SADCT è il percorso più breve con una distanza totale di 11.