Как использовать Z.TEST функцию в Excel
В этой статье мы узнаем, как использовать функцию Z.TEST в Excel.
Что такое проверка гипотез и как использовать Z-тест для проверки гипотез? В статистике проверка гипотез используется для нахождения оценки среднего для набора данных о населении с использованием другой функции распределения, основанной на части набора данных о населении, называемой набором данных о населении. Статистическая гипотеза, иногда называемая подтверждающим анализом данных, — это гипотеза, которую можно проверить на основе наблюдения за процессом, моделируемым с помощью набора случайных величин. Есть два типа гипотез. Одна — нулевая гипотеза, которая является заявленным утверждением, а другая — альтернативная гипотеза, которая прямо противоположна нулевой гипотезе. Например, если мы говорим, что максимальный предел свинца в пакете maggi не должен превышать 225 ppm (частей на миллион), и кто-то утверждает, что существует более фиксированный предел, чем нулевая гипотеза (обозначенная U ~ 0 ~) и альтернативная гипотеза (обозначенная пользователя U ~ a ~)
U ~ 0 ~ = содержание свинца в пакете maggi больше или равно 225 ppm. U ~ a ~ = содержание свинца в пакете maggi менее 225 частей на миллион.
Таким образом, приведенная выше гипотеза является примером правостороннего теста, поскольку основная ситуация находится в правой части кривой распределения.
Если основная ситуация находится на левой стороне, то это будет называться левым тестом. Возьмем еще один пример, иллюстрирующий односторонний тест. Например, если Селина сказала, что может сделать в среднем 60 отжиманий. Теперь вы можете усомниться в этом утверждении и попытаться предположить ситуацию в терминах статистики, тогда нулевая и альтернативная гипотеза изложены ниже U ~ 0 ~ = Селина может сделать 60 отжиманий U ~ a ~ = Селина не может сделать 60 отжиманий Это два подробный тест, в котором основная ситуация лежит по обе стороны заявленного утверждения. Эти хвостовые тесты влияют на результат статистики. Поэтому внимательно выбирайте нулевую и альтернативную гипотезы.
Z — тест Z-тест — это любой статистический тест, для которого распределение тестовой статистики при нулевой гипотезе может быть аппроксимировано нормальным распределением. Z-тест проверяет среднее значение распределения, в котором мы уже знаем дисперсию генеральной совокупности. Из-за центральной предельной теоремы многие статистические данные тестов приблизительно нормально распределяются для больших выборок. Предполагается, что статистика теста имеет нормальное распределение, например, стандартное отклонение должно быть известно для выполнения точного z-теста. Например, инвестор хочет проверить, превышает ли средняя дневная доходность акции 1%, с помощью Z-теста. Z-статистика или Z-оценка * — это число, представляющее, на сколько стандартных отклонений выше или ниже среднего значения для совокупности составляет оценка, полученная с помощью Z-теста. Математически сначала мы решаем нулевую гипотезу и вычисляем Z-балл для распределения по формуле.
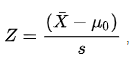
Здесь X (с полосой) — это среднее значение массива выборок. U ~ 0 ~ — это оценочное среднее значение генеральной совокупности. S — стандартное отклонение, где s равно std / (n) ^ 1/2 ^ (где n — размер выборки). .
Как указано выше, Z-тест следует стандартному нормальному распределению. Итак, математически в Excel это следует следующей формуле.
Z.TEST (массив, x, сигма) = 1- Norm.S.Dist ((Average (array) — x) / (sigma / (n) ^ 1/2 ^), TRUE)
или если сигма опущена:
Z.TEST (массив, x) = 1- Norm.S.Dist ((Среднее (массив) — x) / (СТАНДОТКЛОН (массив) / (n) ^ 1/2 ^), ИСТИНА)
где x — выборочное среднее СРЕДНЕЕ (массив), а n — СЧЁТ (массив).
Давайте узнаем, как выполнить Z-тест, используя функцию Z.TEST для вычисления отношения между двумя заданными наборами данных (фактическим и наблюдаемым).
Функция Z.TEST в Excel
Функция Z.TEST возвращает вероятность того, что среднее значение выборки будет больше, чем среднее значение наблюдений в наборе данных (массиве). Функция принимает следующие аргументы.
Z.TEST Синтаксис функции для односторонней вероятности:
|
=Z.TEST ( array , x , [sigma] ) |
Функцию также можно использовать для коммутации двусторонней вероятности.
Z.TEST Синтаксис функции для односторонней вероятности:
|
=2 * MIN(Z.TEST ( array , x , [sigma] ), 1-Z.TEST ( array , x , [sigma] ) ) |
array: образец распределения данных x: значение, для которого оценивается z-критерий [сигма] *: [необязательно] Стандартное отклонение генеральной совокупности (известное). Если не указано, используется стандартное отклонение выборки.
Пример:
Все это может сбивать с толку. Давайте разберемся, как пользоваться функцией, на примере. Здесь у нас есть образец набора данных «Продажи», и нам нужно найти вероятность Z-теста для данного гипотетического среднего значения совокупности, предполагая односторонний тест.
Используйте формулу:
|
= Z.TEST( A2:A9 , C3 ) |
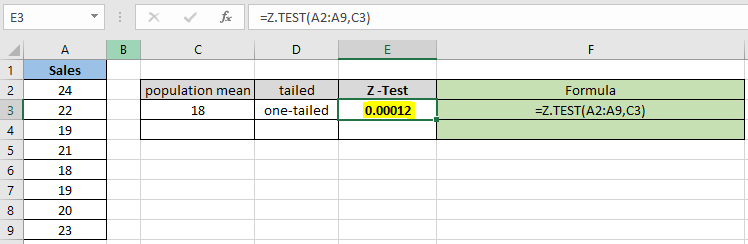
Значение вероятности представлено в десятичном формате, поэтому вы можете преобразовать значение в процент, изменив формат ячейки на процент.
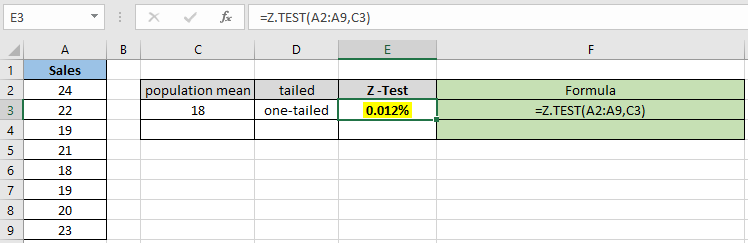
Как вы можете видеть, значение вероятности для гипотетического среднего 18 составляет 0,012% для одностороннего распределения. Теперь вычислите вероятность, предполагая, что двусторонние распределения имеют одинаковые параметры.
Используйте формулу:
|
= 2 * MIN( Z.TEST(A2:A9,C4) , 1 — Z.TEST(A2:A9,C4) ) |
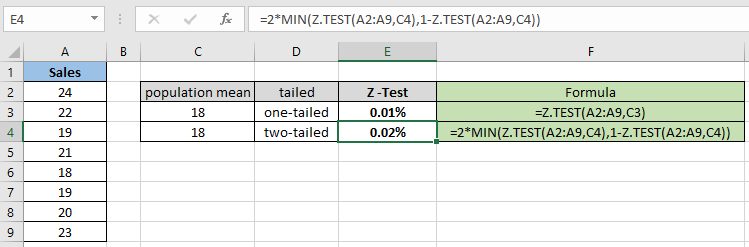
Для двустороннего распределения вероятность удваивается для одного и того же набора данных. Поэтому необходимо проверить нулевую гипотезу и альтернативную гипотезу. Теперь рассчитайте вероятность для различных гипотетических средних значений совокупности и одностороннего распределения.
Используйте формулу:
|
= Z.TEST( A2:A9 , C5 ) |
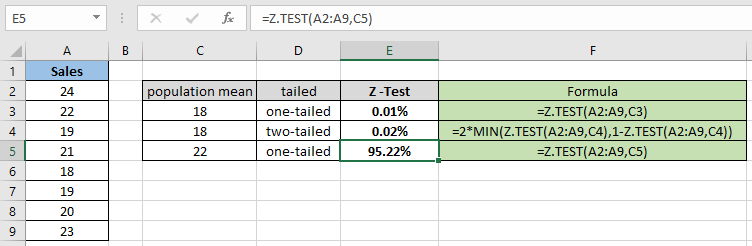
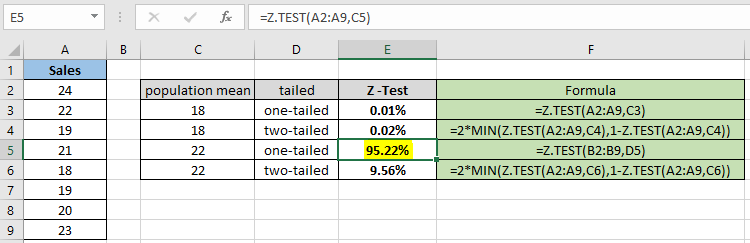
Как вы можете видеть, значение вероятности для гипотетического среднего 22 составляет 95,22% для одностороннего распределения. Теперь вычислите вероятность, предполагая, что двусторонние распределения имеют одинаковые параметры.
Используйте формулу:
|
= 2 * MIN( Z.TEST(A2:A9,C6) , 1 — Z.TEST(A2:A9,C6) ) |
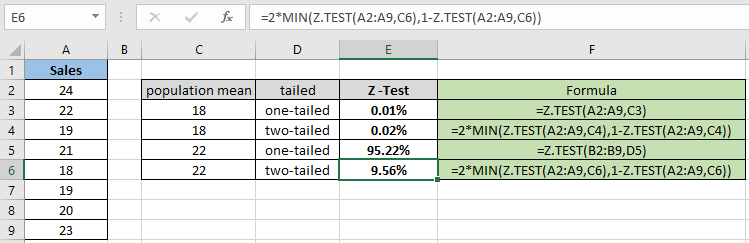
Как вы можете отличить от приведенного выше снимка, значение вероятности становится меньше при вычислении двустороннего распределения. Функция возвращает 9,56% для предполагаемого среднего значения для населения 22.
Z.TEST представляет вероятность того, что среднее значение выборки будет больше наблюдаемого значения AVERAGE (массив), когда базовое среднее значение генеральной совокупности равно 0. Исходя из симметрии нормального распределения, если AVERAGE (массив) <x, Z.TEST будет вернуть значение больше 0,5.
Вот все заметки с использованием функции Z.TEST в Excel
Примечания:
-
Функция работает только с числами. Если среднее значение генеральной совокупности или аргумент сигма не являются числовыми, функция возвращает # ЗНАЧ! ошибка.
-
Десятичное значение или значение в процентах — это то же значение в Excel.
При необходимости преобразуйте значение в проценты.
-
Функция возвращает # ЧИСЛО! Ошибка, если аргумент сигмы равен 0.
-
Функция возвращает # Н / Д! Ошибка, если предоставленный массив пуст.
-
Функция возвращает # DIV / 0! Ошибка, .. Если стандартное отклонение массива равно 0 и аргумент сигма опущен.
-
Если массив содержит только одно значение.
-
Надеюсь, эта статья о том, как использовать функцию Z.TEST в Excel, носит пояснительный характер. Дополнительные статьи о статистических формулах и связанных функциях Excel можно найти здесь. Если вам понравились наши блоги, поделитесь ими с друзьями на Facebook. А также вы можете подписаться на нас в Twitter и Facebook. Мы будем рады услышать от вас, дайте нам знать, как мы можем улучшить, дополнить или усовершенствовать нашу работу и сделать ее лучше для вас. Напишите нам на [email protected].
Статьи по теме:
link: / statistics-formulas-how-to-use-t-test-function-in-excel [Как использовать функцию TEST в Excel в Excel]: T.TEST используется для определения достоверности анализа. Математически он используется, чтобы узнать, равны ли средние двух выборок или нет. T.TEST используется для принятия или отклонения нулевой гипотезы.
link: / statistics-formulas-how-to-use-excel-f-test-function [Как использовать функцию Excel F.TEST в Excel]: Функция F.TEST используется для вычисления F-статистики двух выборок в excel внутренне и возвращает двустороннюю вероятность F-статистики при нулевой гипотезе.
link: / statistics-formulas-how-to-use-the-devsq-function-in-excel [Как использовать функцию DEVSQ в Excel]: функция DEVSQ — это встроенная статистическая функция для вычисления суммы квадратов отклонения от среднего или среднего диапазона предоставленных значений данных.
link: / statistics-formulas-how-to-use-excel-normdist-function [Как использовать функцию НОРМ.РАСП в Excel]: вычислить балл Z для нормального кумулятивного распределения для предварительно указанных значений с помощью функции НОРМРАСП в Excel.
link: / statistics-formulas-how-to-use-excel-norm-inv-function [Как использовать функцию Excel NORM.INV]: вычислить обратную оценку Z для нормального кумулятивного распределения для предварительно заданной вероятности значения с помощью функции НОРМ.ОБР в Excel.
link: / excel-financial-formulas-how-to-calculate-standard-deviation-in-excel [Как рассчитать стандартное отклонение в Excel]: * Для вычисления стандартного отклонения в Excel есть различные функции. Стандартное отклонение — это квадратный корень из значения дисперсии, но он больше говорит о наборе данных, чем дисперсия.
link: / statistics-formulas-excel-var-function [Как использовать функцию VAR в Excel]: вычислить дисперсию для образца набора данных в Excel с помощью функции VAR в Excel.
Популярные статьи:
link: / tips-if-condition-in-excel [Как использовать функцию IF в Excel]: оператор IF в Excel проверяет условие и возвращает конкретное значение, если условие истинно, или другое конкретное значение, если оно ложно .
link: / formulas-and-functions-Introduction-of-vlookup-function [Как использовать функцию ВПР в Excel]: Это одна из наиболее часто используемых и популярных функций Excel, которая используется для поиска значений из разных диапазонов и листы. link: / excel-formula-and-function-excel-sumif-function [Как использовать функцию СУММЕСЛИ в Excel]: Это еще одна важная функция информационной панели. Это поможет вам суммировать значения для конкретных условий.
link: / tips-countif-in-microsoft-excel [Как использовать функцию СЧЁТЕСЛИ в Excel]: Подсчет значений с условиями с помощью этой удивительной функции. Вам не нужно фильтровать данные для подсчета определенных значений. Функция Countif важна для подготовки вашей приборной панели.