В этой статье мы узнаем, как рассчитать средневзвешенное значение в Microsoft Excel.

Понятие среднего происходит из математики. Среднее значение можно определить как результат, который мы получаем после сложения нескольких величин и последующего деления этой суммы на количество величин.

Средневзвешенное значение аналогично среднему арифметическому, где вместо того, чтобы каждая из точек данных вносила равный вклад в окончательное среднее значение, некоторые точки данных вносили больший вклад, чем другие.

Если все веса равны, то средневзвешенное значение остается таким же, как и среднее арифметическое.

Давайте разберемся на примере:

Мы хотим вычислить среднее значение оценок учащегося по четырем предметам. * В столбце A есть тема, а в столбце B — оценки

img1

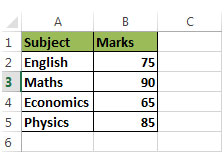
Мы сложим числа, а затем разделим результат на количество испытуемых (75 + 90 + 65 + 85) / 4 = 78,5 * Это невзвешенное среднее значение, потому что в этом сценарии мы присвоили каждому числу одинаковый приоритет.

Средневзвешенное значение — это тип среднего, в котором элемент веса также учитывается при нахождении среднего, потому что этот один элемент может значительно повлиять на конечный результат, чем другой элемент.

А теперь давайте разберемся с другим примером

В столбце A у нас есть тема & в столбце B, у нас есть оценки

img2

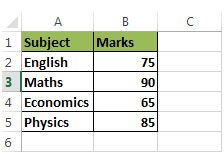
Предположим, что студент хочет поступить в математический колледж из-за интереса к математике. Команда колледжа осознала, что более высокий процент студентов хотят поступить в свой колледж из-за хороших доступных факультетов и их отличной репутации по математике. Таким образом, очевидно, что колледж будет уделять больше внимания оценкам по математике, и, следовательно, они придумали идею присвоения веса каждому предмету следующим образом:

img3

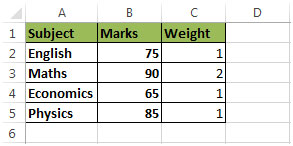
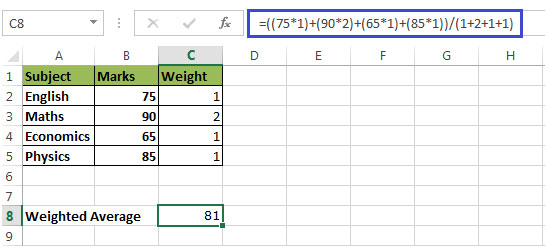
Это показывает, что колледж уделяет больше внимания оценкам по математике по сравнению с оценками по другим предметам. Если мы умножим оценки на вес, то есть (оценки x вес), мы получим: 75 x 1) + (90 x 2) + (65 x 1) + (85 x 1 / (1 + 2 + 1 + 1)

  • Получится 81

img4

  • Средневзвешенное значение (81) выше невзвешенного среднего (78,5)

  • Итак, в этом случае оценки по математике повлияли на конечный результат больше, чем любой другой элемент.

  • В показанном выше примере мы поняли разницу между взвешенным и невзвешенным средним.