Sơ đồ hộp và chiếc râu trong Excel
Simple Box and Whisker Plot
-
Ví dụ: chọn phạm vi A1: A7.
Lưu ý: bạn không cần phải sắp xếp các điểm dữ liệu từ nhỏ nhất đến lớn nhất, nhưng nó sẽ giúp bạn hiểu được âm mưu của hộp và râu.
-
Trên tab Chèn, trong nhóm Biểu đồ, hãy bấm vào biểu tượng Biểu đồ Thống kê.

-
Nhấp vào Hộp và Râu.
Kết quả:
Giải thích: dòng giữa của hộp thể hiện số trung vị hoặc số giữa (8). Dấu x trong hộp biểu thị giá trị trung bình (cũng là 8 trong ví dụ này). Đường trung bình chia tập dữ liệu thành nửa dưới \ {2, 4, 5} và nửa trên \ {10, 12, 15}. Dòng dưới cùng của hộp biểu thị giá trị trung bình của nửa dưới hoặc phần tư thứ nhất (4). Dòng trên cùng của hộp biểu thị giá trị trung bình của nửa trên hoặc phần tư thứ 3 (12). Râu (đường thẳng đứng) kéo dài từ hai đầu hộp đến giá trị nhỏ nhất (2) và giá trị lớn nhất (15).
Ngoại lệ
-
Ví dụ: chọn phạm vi A1: A11.
Lưu ý: số trung vị hoặc số giữa (8) chia tập dữ liệu thành hai nửa: \ {1, 2, 2, 4, 5} và \ {10, 12, 15, 18, 35}. Phần tư thứ nhất (Q ~ 1 ~) là trung bình của hiệp một. Q ~ 1 ~ = 2. Phần tư thứ 3 (Q ~ 3 ~) là trung vị của nửa sau. Q ~ 3 ~ = 15.
-
Trên tab Chèn, trong nhóm Biểu đồ, hãy bấm vào biểu tượng Biểu đồ Thống kê.

-
Nhấp vào Hộp và Râu.

Kết quả:
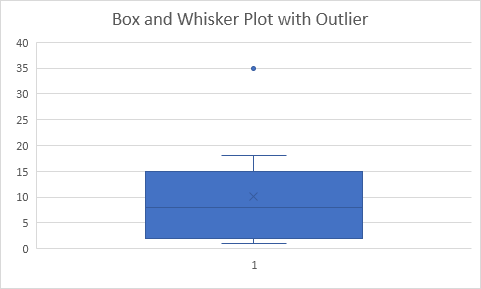
Giải thích: phạm vi liên phần tư (IQR) được định nghĩa là khoảng cách giữa phần tư thứ nhất và phần tư thứ ba. Trong ví dụ này, IQR = Q ~ 3 ~ – Q ~ 1 ~ = 15 – 2 = 13. Một điểm dữ liệu được coi là ngoại lệ nếu nó vượt quá khoảng cách 1,5 lần IQR bên dưới phần tư thứ nhất (Q ~ 1 ~ – 1,5 IQR = 2 – 1,5 13 = -17,5) hoặc 1,5 lần IQR trên phần tư thứ 3 (Q ~ 3 ~ + 1,5 IQR = 15 + 1,5 13 = 34,5). Do đó, trong ví dụ này, 35 được coi là giá trị ngoại lệ. Do đó, râu trên mở rộng đến giá trị lớn nhất (18) trong phạm vi này.
-
Thay đổi điểm dữ liệu cuối cùng thành 34.
Kết quả:
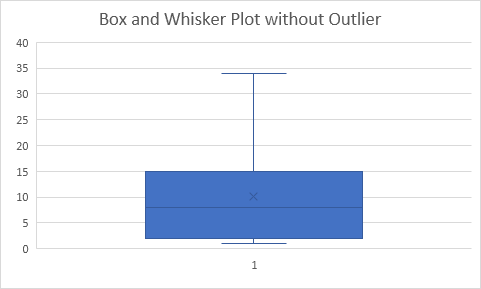
Giải thích: tất cả các điểm dữ liệu nằm trong khoảng -17,5 đến 34,5. Kết quả là, râu mở rộng đến giá trị nhỏ nhất (2) và giá trị lớn nhất (34).
Tính toán lô đất
Hầu hết thời gian, bạn không thể dễ dàng xác định phần tư thứ nhất và phần tư thứ ba nếu không thực hiện các phép tính.
-
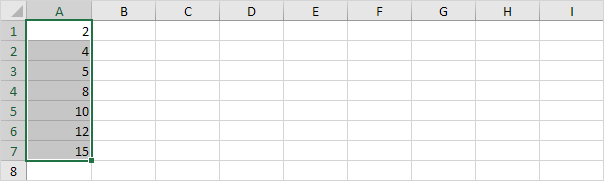
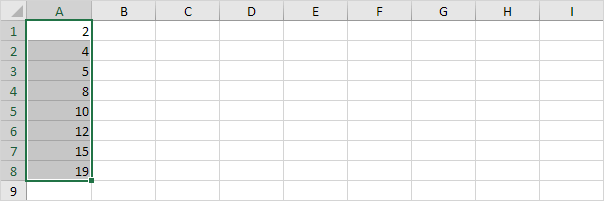
Ví dụ: chọn số điểm dữ liệu chẵn bên dưới.
-
Trên tab Chèn, trong nhóm Biểu đồ, hãy bấm vào biểu tượng Biểu đồ Thống kê.

-
Nhấp vào Hộp và Râu.

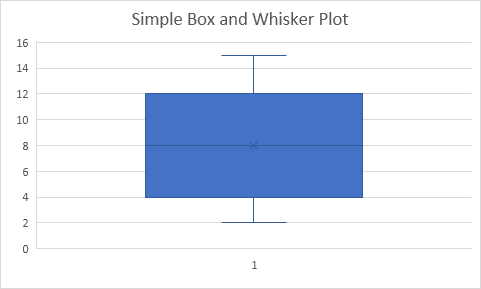
Kết quả:
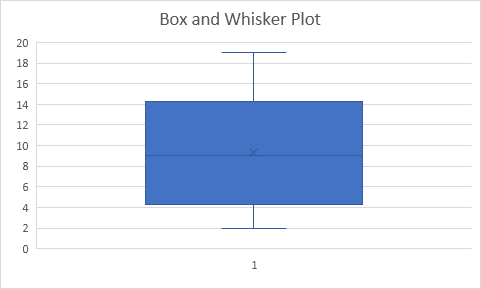
Giải thích: Excel sử dụng hàm QUARTILE.EXC để tính phần tư thứ nhất (Q ~ 1 ~), phần tư thứ 2 (Q ~ 2 ~ hoặc trung vị) và phần tư thứ 3 (Q ~ 3 ~).
Hàm này nội suy giữa hai giá trị để tính một phần tư.
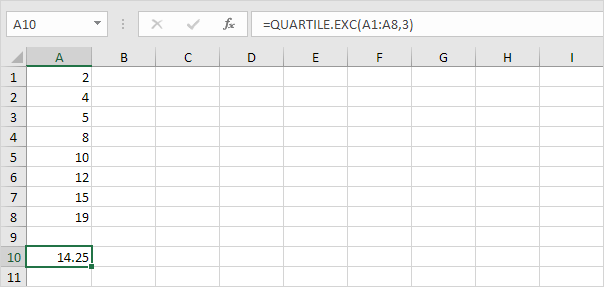
Trong ví dụ này, n = 8 (số điểm dữ liệu).
-
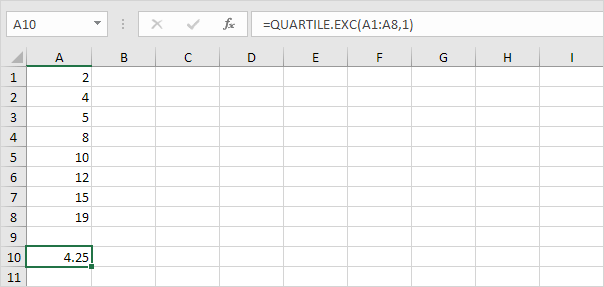
Giá trị thứ Q ~ 1 ~ = 1/4 (n + 1) = 1/4 (8 + 1) giá trị thứ = 2 1/4 Giá trị thứ 4 = 4 + 1/4 (5-4) = 4 1/4 . Bạn có thể xác minh con số này bằng cách sử dụng hàm QUARTILE.EXC hoặc xem hộp và biểu đồ râu ria.
-
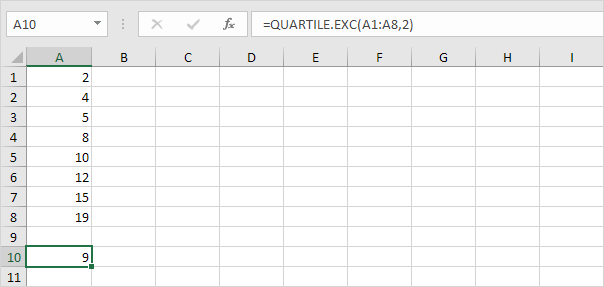
Giá trị thứ Q ~ 2 ~ = 1/2 (n + 1) = 1/2 (8 + 1) giá trị thứ = 4 Giá trị 1/2 = 8 + 1/2 (10-8) = 9. Điều này làm cho giác, trung vị là trung bình cộng của hai số ở giữa.
-
Giá trị thứ Q ~ 3 ~ = 3/4 (n + 1) = 3/4 (8 + 1) giá trị thứ = 6 Giá trị 3/4 = 12 + 3/4 * (15-12) = 14 1 / 4. Một lần nữa, bạn có thể xác minh con số này bằng cách sử dụng hàm QUARTILE.EXC hoặc xem hộp và biểu đồ râu ria.