Cách sử dụng hàm IRR
Sử dụng hàm IRR trong Excel để tính tỷ lệ hoàn vốn nội bộ của dự án. Tỷ suất hoàn vốn nội bộ là tỷ suất chiết khấu làm cho giá trị hiện tại ròng bằng không.
Ví dụ IRR đơn giản
Ví dụ: dự án A yêu cầu vốn đầu tư ban đầu là 100 đô la (ô B5).
-
Chúng tôi kỳ vọng lợi nhuận $ 0 vào cuối kỳ đầu tiên, lợi nhuận $ 0 vào cuối kỳ thứ hai và lợi nhuận là $ 152,09 vào cuối kỳ thứ ba.
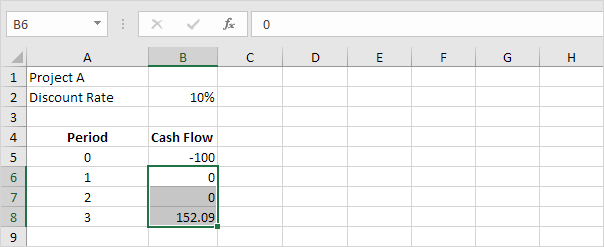
Lưu ý: tỷ lệ chiết khấu bằng 10%. Đây là tỷ suất sinh lợi của khoản đầu tư thay thế tốt nhất. Ví dụ, bạn cũng có thể gửi tiền vào tài khoản tiết kiệm với lãi suất 10%.
-
Liên kết
đúng: /amples-npv [công thức NPV]trong Excel sử dụng hàm NPV để tính giá trị hiện tại của một loạt các dòng tiền trong tương lai và trừ đi khoản đầu tư ban đầu.
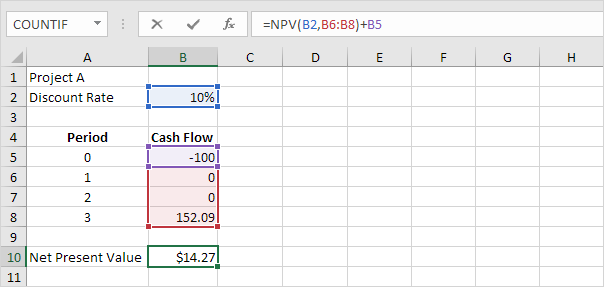
Giải thích: giá trị hiện tại ròng dương chỉ ra rằng tỷ suất sinh lợi của dự án vượt quá tỷ suất chiết khấu. Nói cách khác, đầu tư tiền của bạn vào dự án A tốt hơn là gửi tiền vào tài khoản tiết kiệm với lãi suất 10%.
-
Hàm IRR dưới đây tính toán tỷ suất hoàn vốn nội bộ của dự án A.
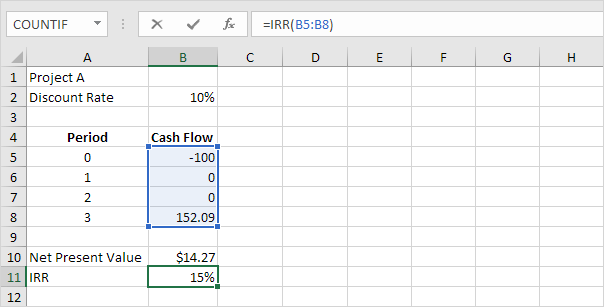
-
Tỷ suất hoàn vốn nội bộ là tỷ lệ chiết khấu làm cho giá trị hiện tại ròng bằng không. Để thấy rõ điều này, hãy thay tỷ lệ chiết khấu 10% trong ô B2 bằng 15%.
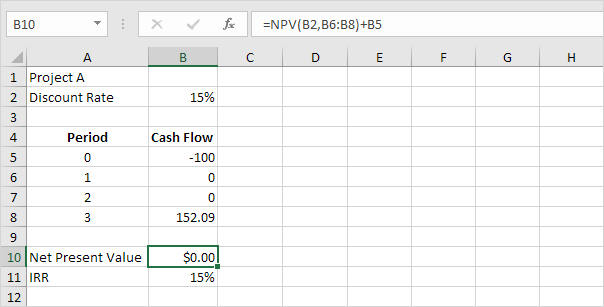
Giải thích: giá trị hiện tại ròng bằng 0 chỉ ra rằng dự án tạo ra tỷ suất sinh lợi bằng với tỷ suất chiết khấu. Nói cách khác, cả hai lựa chọn, đầu tư tiền của bạn vào dự án A hoặc gửi tiền của bạn vào một tài khoản tiết kiệm năng suất cao với lãi suất 15%, đều mang lại lợi nhuận như nhau.
-
Chúng tôi có thể kiểm tra điều này. Giả sử bạn gửi 100 đô la vào ngân hàng. Khoản đầu tư của bạn sẽ có giá trị bao nhiêu sau 3 năm với lãi suất hàng năm là 15%? Câu trả lời là $ 152,09.
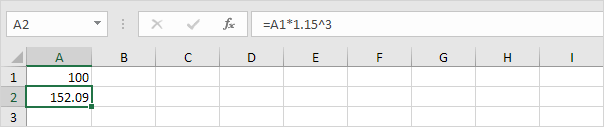
Kết luận: bạn có thể so sánh hiệu suất của một dự án với một tài khoản tiết kiệm có lãi suất bằng IRR.
Giá trị hiện tại
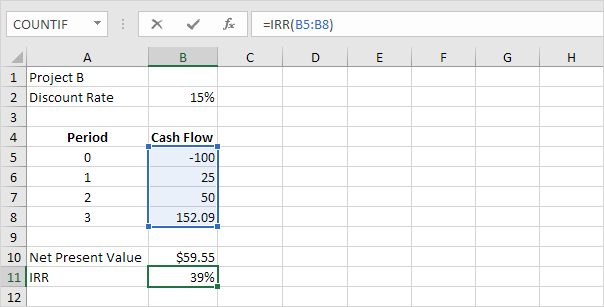
Ví dụ: dự án B yêu cầu đầu tư ban đầu là 100 đô la (ô B5).
Chúng tôi kỳ vọng lợi nhuận là $ 25 vào cuối kỳ đầu tiên, lợi nhuận $ 50 vào cuối kỳ thứ hai và lợi nhuận là $ 152,09 vào cuối kỳ thứ ba.
-
Hàm IRR dưới đây tính toán tỷ suất hoàn vốn nội bộ của dự án B.
-
Một lần nữa, tỷ suất hoàn vốn nội bộ là tỷ suất chiết khấu làm cho giá trị hiện tại ròng bằng không. Để thấy rõ điều này, hãy thay tỷ lệ chiết khấu 15% trong ô B2 bằng 39%.
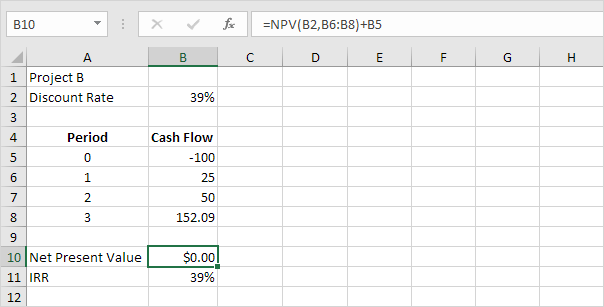
Giải thích: giá trị hiện tại ròng bằng 0 chỉ ra rằng dự án tạo ra tỷ suất sinh lợi bằng với tỷ suất chiết khấu. Nói cách khác, cả hai lựa chọn, đầu tư tiền của bạn vào dự án B hoặc gửi tiền của bạn vào một tài khoản tiết kiệm năng suất cao với lãi suất 39%, đều mang lại lợi nhuận như nhau.
-
Chúng tôi có thể kiểm tra điều này. Đầu tiên, chúng tôi tính giá trị hiện tại (pv) của mỗi dòng tiền. Tiếp theo, chúng tôi tính tổng các giá trị này.
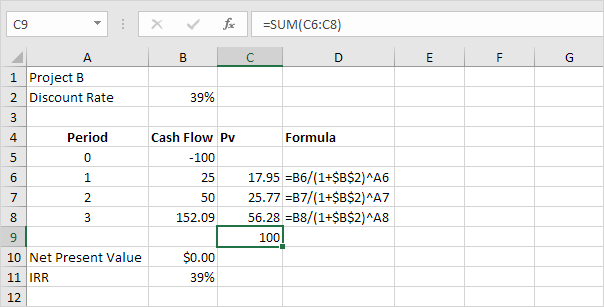
Giải thích: thay vì đầu tư 100 đô la vào dự án B, bạn cũng có thể gửi 17,95 đô la vào tài khoản tiết kiệm trong 1 năm, 25,77 đô la vào tài khoản tiết kiệm trong 2 năm và 56,28 đô la vào tài khoản tiết kiệm trong ba năm, với lãi suất hàng năm bằng IRR (39%).
Quy tắc IRR
Quy tắc IRR nêu rõ rằng nếu IRR lớn hơn tỷ lệ hoàn vốn yêu cầu, bạn nên chấp nhận dự án. Giá trị IRR thường được sử dụng để so sánh các khoản đầu tư.
-
Hàm IRR dưới đây tính toán tỷ suất hoàn vốn nội bộ của dự án X.
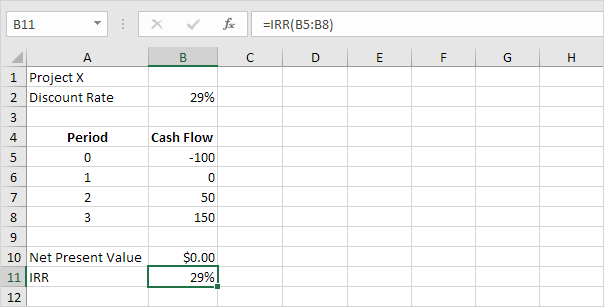
Kết luận: nếu tỷ suất sinh lợi yêu cầu bằng 15%, bạn nên chấp nhận dự án này vì IRR của dự án này bằng 29%.
-
Hàm IRR dưới đây tính toán tỷ suất hoàn vốn nội bộ của dự án Y.
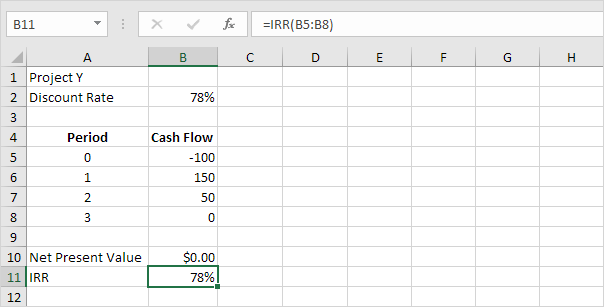
Kết luận: nói chung, IRR cao hơn cho thấy một khoản đầu tư tốt hơn.
Do đó, dự án Y là một khoản đầu tư tốt hơn dự án X.
-
Hàm IRR dưới đây tính toán tỷ suất hoàn vốn nội bộ của dự án Z.
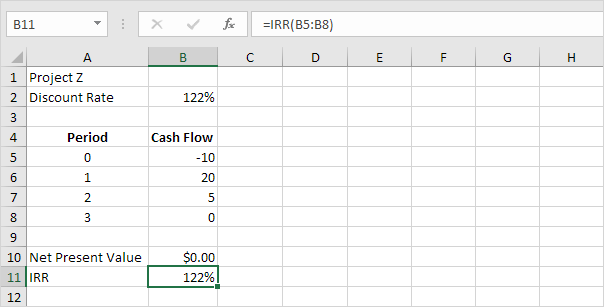
Kết luận: IRR cao hơn không phải lúc nào cũng tốt hơn. Dự án Z có IRR cao hơn dự án Y nhưng dòng tiền thấp hơn nhiều.