Ví dụ này hướng dẫn bạn cách chạy phân tích hồi quy tuyến tính trong Excel và cách diễn giải Kết quả tóm tắt.

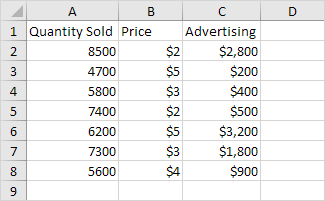
Dưới đây bạn có thể tìm thấy dữ liệu của chúng tôi. Câu hỏi lớn đặt ra là: Liệu có mối quan hệ giữa Số lượng Bán (Đầu ra) với Giá cả và Quảng cáo (Đầu vào). Nói cách khác: chúng ta có thể dự đoán Số lượng Bán được nếu chúng ta biết Giá cả và Quảng cáo?

Regression Data in Excel

  1. Trên tab Dữ liệu, trong nhóm Phân tích, hãy bấm Phân tích Dữ liệu.

Click Data Analysis

Lưu ý: không tìm thấy nút Phân tích dữ liệu? Nhấp vào đây để tải bổ trợ Analysis ToolPak.

  1. Chọn Hồi quy và nhấp OK.

Select Regression

  1. Chọn Dãy Y (A1: A8). Đây là biến dự báo (còn gọi là biến phụ thuộc).

  2. Chọn Dãy X (B1: C8). Đây là các biến giải thích (còn gọi là biến độc lập). Các cột này phải liền kề nhau.

  3. Kiểm tra Nhãn.

  4. Nhấp vào hộp Phạm vi đầu ra và chọn ô A11.

  5. Kiểm tra phần dư.

  6. Nhấp vào OK.

Regression Input and Output

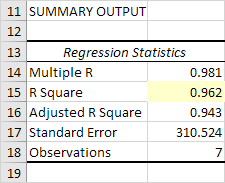
Excel tạo ra Kết quả Tóm tắt sau (làm tròn đến 3 chữ số thập phân).

R Square

R Square bằng 0,962, rất phù hợp. 96% sự thay đổi về Số lượng Bán được giải thích bởi các biến độc lập Giá và Quảng cáo. Càng gần 1, dòng hồi quy (đọc tiếp) càng phù hợp với dữ liệu.

R Square

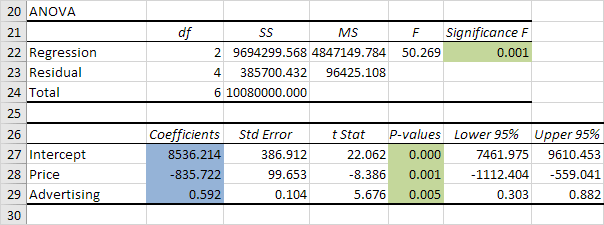
Ý nghĩa F và giá trị P

Để kiểm tra xem kết quả của bạn có đáng tin cậy (có ý nghĩa thống kê) hay không, hãy nhìn vào Mức độ có nghĩa F (0,001). Nếu giá trị này nhỏ hơn 0,05, bạn không sao.

Nếu Significance F lớn hơn 0,05, có lẽ tốt hơn nên ngừng sử dụng tập hợp các biến độc lập này. Xóa một biến có giá trị P cao (lớn hơn 0,05) và chạy lại hồi quy cho đến khi Mức ý nghĩa F giảm xuống dưới 0,05.

Hầu hết hoặc tất cả các giá trị P phải dưới 0,05. Trong ví dụ của chúng tôi, đây là trường hợp. (0,000, 0,001 và 0,005).

Anova

Hệ số

Đường hồi quy là: y = Số lượng Bán = 8536.214 -835.722 Giá + 0,592 Quảng cáo. Nói cách khác, với mỗi đơn vị tăng giá, Số lượng bán được giảm đi 835,722 đơn vị. Đối với mỗi đơn vị quảng cáo tăng, Số lượng bán tăng với 0,592 đơn vị. Đây là thông tin có giá trị.

Bạn cũng có thể sử dụng các hệ số này để dự báo. Ví dụ: nếu giá bằng 4 đô la và Quảng cáo bằng 3000 đô la, bạn có thể đạt được Số lượng đã bán là 8536.214 -835.722 4 + 0.592 3000 = 6970.

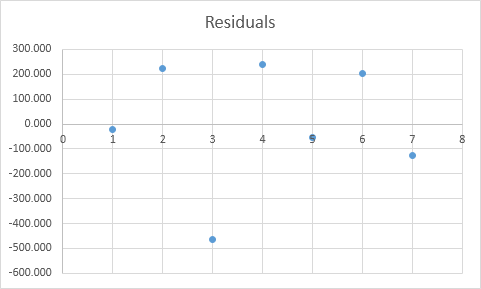
Dư

Các phần còn lại cho bạn thấy các điểm dữ liệu thực tế cách các điểm dữ liệu dự đoán (sử dụng phương trình) bao xa. Ví dụ: điểm dữ liệu đầu tiên bằng 8500. Sử dụng phương trình, điểm dữ liệu dự đoán bằng 8536.214 -835.722 2 + 0.592 2800 = 8523.009, cho số dư là 8500 – 8523.009 = -23.009.

Residuals

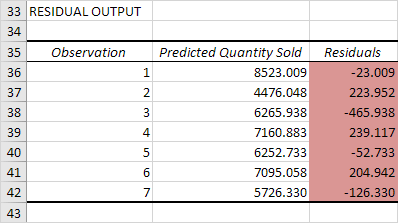
Bạn cũng có thể tạo một biểu đồ phân tán của những phần còn lại này.

Scatter Plot