Vấn đề về đường dẫn ngắn nhất trong Excel
Sử dụng bộ giải trong Excel để tìm đường đi ngắn nhất từ nút S đến nút T trong một mạng vô hướng. Các điểm trong mạng được gọi là các nút (S, A, B, C, D, E và T). Các đường trong mạng được gọi là cung (SA, SB, SC, AC, v.v.).
Hình thành mô hình
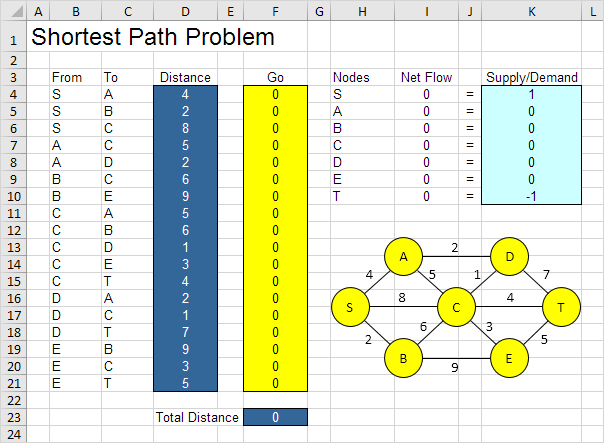
Mô hình chúng ta sẽ giải quyết trông như sau trong Excel.
-
Để hình thành bài toán về con đường ngắn nhất này, hãy trả lời ba câu hỏi sau.
\ a. Các quyết định được thực hiện là gì? Đối với vấn đề này, chúng ta cần Excel để tìm xem một cung có nằm trên đường ngắn nhất hay không (Có = 1, Không = 0). Ví dụ: nếu SB là một phần của đường đi ngắn nhất, ô F5 bằng 1. Nếu không, ô F5 bằng 0.
\ b. Những ràng buộc đối với những quyết định này là gì? Lưu lượng ròng (Dòng ra – Dòng vào) của mỗi nút phải bằng Cung / Cầu. Nút S chỉ nên có một cung đi ra (Net Flow = 1). Nút T chỉ nên có một vòng cung đang chạy (Net Flow = -1). Tất cả các nút khác phải có một cung đi ra và một cung đi vào nếu nút nằm trên đường ngắn nhất (Luồng ròng = 0) hoặc không có luồng nào (Luồng ròng = 0).
\ c. Thước đo tổng thể về hiệu suất cho những quyết định này là gì? Số đo tổng thể của hiệu suất là tổng khoảng cách của đường đi ngắn nhất, vì vậy mục tiêu là giảm thiểu đại lượng này.
-
Để làm cho mô hình dễ hiểu hơn, hãy đặt tên cho các phạm vi sau.
|
Range Name |
Cells |
|
From |
B4:B21 |
|
To |
C4:C21 |
|
Distance |
D4:D21 |
|
Go |
F4:F21 |
|
NetFlow |
I4:I10 |
|
SupplyDemand |
K4:K10 |
|
TotalDistance |
F23 |
-
Chèn các chức năng sau.
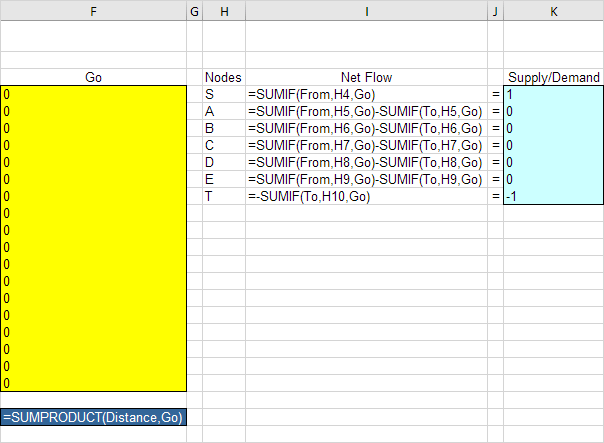
Thử và Lỗi
Với công thức này, việc phân tích bất kỳ dung dịch thử nào trở nên dễ dàng.
-
Ví dụ, đường dẫn SBET có tổng khoảng cách là 16.
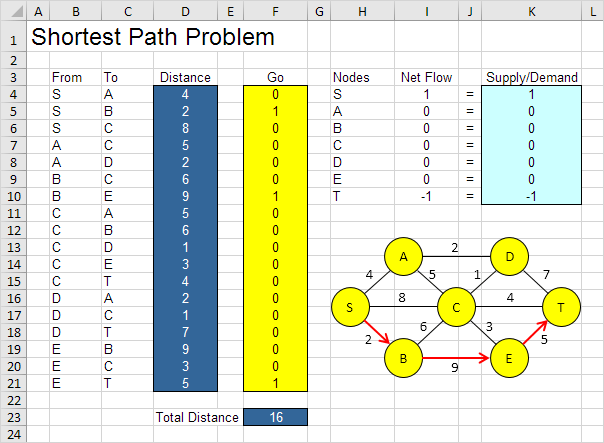
Không nhất thiết phải sử dụng thử và sai. Tiếp theo, chúng tôi sẽ mô tả cách sử dụng Excel Solver để nhanh chóng tìm ra giải pháp tối ưu.
Giải quyết mô hình
Để tìm ra giải pháp tối ưu, hãy thực hiện các bước sau.
-
Trên tab Dữ liệu, trong nhóm Phân tích, hãy bấm Bộ giải.
Lưu ý: không tìm thấy nút Solver? Nhấp vào đây để tải phần bổ trợ Solver.
Nhập các thông số của bộ giải (đọc tiếp). Kết quả phải phù hợp với hình dưới đây.
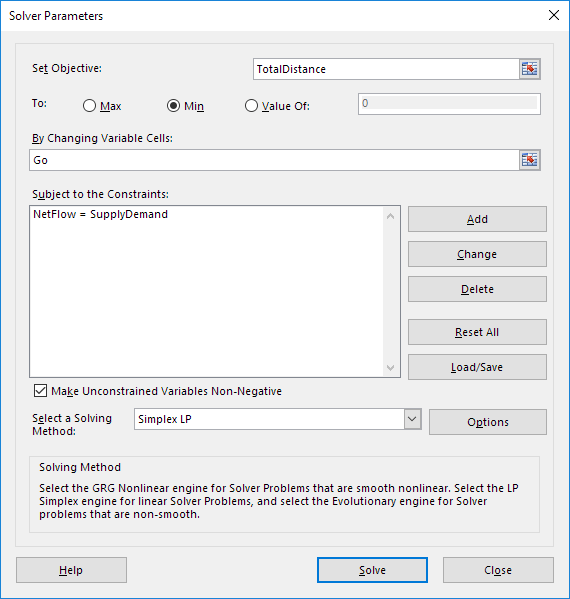
Bạn có thể chọn nhập tên phạm vi hoặc nhấp vào các ô trong bảng tính.
-
Nhập TotalDistance cho Mục tiêu.
-
Nhấp vào Min.
-
Nhập Go cho các ô có thể thay đổi.
-
Nhấp vào Thêm để nhập ràng buộc sau.
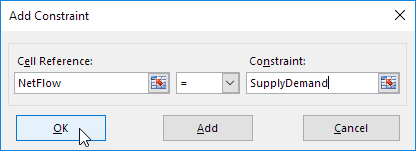
-
Kiểm tra ‘Làm cho các biến không bị ràng buộc thành không phủ định’ và chọn ‘Simplex LP’.
-
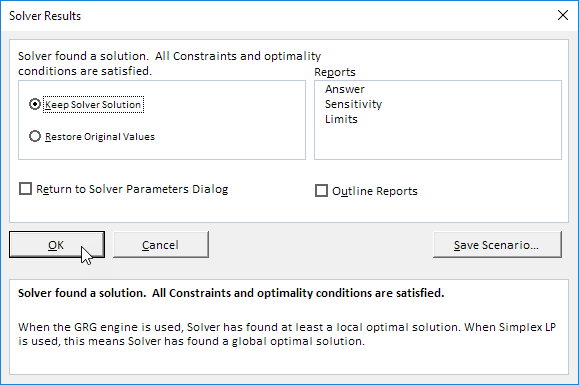
Cuối cùng, nhấp vào Giải quyết.
Kết quả:
Giải pháp tối ưu:
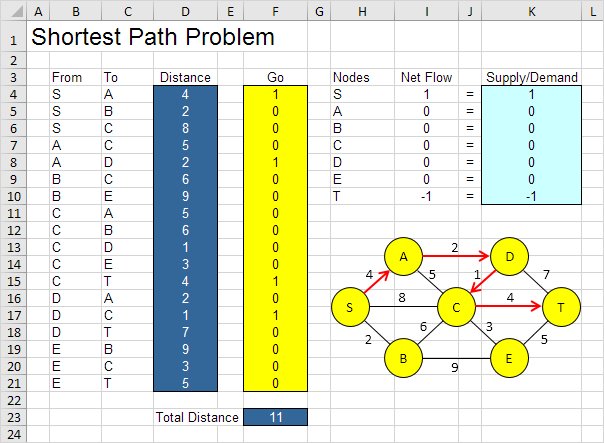
Kết luận: SADCT là đường đi ngắn nhất với tổng khoảng cách là 11.