Cách sử dụng hàm BINOM.INV trong Excel

Trong bài viết này, chúng ta sẽ tìm hiểu Cách sử dụng hàm BINOM.INV trong Excel.
Phân phối xác suất nhị thức và nghịch đảo của phân phối tích lũy nhị thức là gì? Phân phối nhị thức là một thước đo thống kê chủ yếu được sử dụng để tìm xác suất của một số thành công xảy ra từ số lần thử nghiệm độc lập. Ví dụ: có hai kết quả của một sự kiện, hoặc thành công được biểu thị bằng p, hoặc thất bại được biểu thị bằng 1-p *.
Xác suất p có thể nhận giá trị trong khoảng [0, 1]. Công thức toán học để tìm giá trị kỳ vọng cho phân phối nhị thức của sự kiện xảy ra trong phép thử độc lập x * được hiển thị bên dưới.
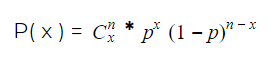
Ở đây C là hàm tổ hợp có thể được dịch là n! / (x! * (n-x)!) đâu! là biểu tượng cho hàm giai thừa.
Công thức trên được sử dụng để tính xác suất của một sự kiện xảy ra trong x thử nghiệm độc lập. Đối với hàm trên, bạn có thể sử dụng hàm BINOM.DIST trong Excel. Bây giờ, lấy nghịch đảo của hàm đã nêu ở trên, chúng ta có thể tính số thử nghiệm nhỏ nhất cần thiết mà phân phối nhị thức tích lũy hoặc giá trị tới hạn cho phân phối nhị thức lớn hơn hoặc bằng một giá trị tiêu chí hoặc alpha. Ví dụ, nghịch đảo của phân phối tích lũy nhị thức có thể được sử dụng để tính số lần tung đồng xu tối thiểu mà có 50% cơ hội có ít nhất 20 đầu. Bây giờ bạn sẽ hiểu cách tính số lần thử nhỏ nhất hoặc số sự kiện, số lần thử để có thành công đầu tiên bằng cách sử dụng hàm BINOM.INV.
Hàm BINOM.INV trong Excel
BINOM.INV là một hàm thống kê trả về giá trị nhỏ nhất của các thử nghiệm mà hàm Phân phối nhị thức tích lũy là một xác suất nhất định.
BINOM.INV Cú pháp hàm:
|
=BINOM.INV(trials, probability_s, alpha) |
Thử nghiệm: Số lượng thử nghiệm độc lập.
Probability_s: Xác suất thành công của mỗi lần thử.
alpha: giá trị tiêu chí, xác suất của Phân phối nhị thức tích lũy (phải từ 0 đến 1).
Ví dụ:
Tất cả những điều này có thể khó hiểu. Hãy hiểu cách sử dụng hàm bằng một ví dụ. Ở đây chúng ta có một tình huống mà chúng ta có 2 quả bóng đỏ và 3 quả bóng trắng trong một túi. Chúng tôi bắt đầu một sự kiện trong đó chúng tôi lấy ra một quả bóng từ túi và ghi lại màu sắc của nó và đặt quả bóng trở lại túi. Nếu chúng ta lặp lại nhiệm vụ 10 lần. Hiện tại, chúng tôi muốn biết số lần thử nhỏ nhất hoặc tối thiểu có thể được yêu cầu để lấy được quả bóng đỏ. Vì vậy, để hàm BINOM.INV được sử dụng, chúng ta có một số phép thử, xác suất thành công và xác suất alpha. Đối với điều đó, chúng tôi sử dụng công thức cơ bản của xác suất.
Sử dụng công thức:
|
= number of red balls / total number of balls |
Cái này sẽ được hiểu là = B2 / B1 *.
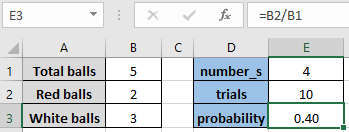
Như bạn thấy, xác suất để một quả bóng màu đỏ xuất hiện là 0,40 *.
Sử dụng giá trị xác suất này, chúng tôi muốn số lần thử tối thiểu cần thiết để lấy được quả bóng màu đỏ. Bây giờ chúng ta sẽ sử dụng hàm BINOM.INV với các tham số đã cho.
Sử dụng công thức:
|
=BINOM.INV( C1, C2, C3) |

Như bạn thấy, số lần thử tối thiểu cần thiết là 4, điều này chắc chắn sẽ trả về quả bóng màu đỏ hoặc nếu không hãy kiểm tra lại túi. trong khi xác suất để tìm thấy quả bóng màu đỏ trong 4 lần thử tiếp theo hoặc phân phối tích lũy của nhị thức là 0,63 *. Bạn có thể sử dụng hàm cho bất kỳ hàm xác suất hoặc hàm tích lũy nào. Sử dụng hàm BINOM.DIST để tính giá trị xác suất cho phân phối nhị thức.
Dưới đây là tất cả các lưu ý quan sát bằng cách sử dụng hàm BINOM.INV trong Excel
Ghi chú:
-
Hàm chỉ hoạt động với các số.
-
Nạp trực tiếp các đối số hoặc sử dụng tham chiếu ô như đã nêu trong ví dụ trên.
-
Hàm BINOM.INV là phiên bản cập nhật của hàm CRITBINOM.
-
thử nghiệm được cắt ngắn thành số nguyên.
-
Nếu alpha, lần thử hoặc xác suất_s không phải là số, BINOM.INV trả về giá trị lỗi #VALUE! giá trị lỗi.
-
Nếu alpha <0 hoặc alpha> 1, BINOM.INV trả về giá trị lỗi #NUM! giá trị lỗi.
-
Nếu xác suất_s <0 hoặc xác suất_s> 1, hàm BINOM.INV trả về giá trị lỗi #NUM!
giá trị lỗi.
Hy vọng bài viết này về Cách sử dụng hàm BINOM.INV trong Excel là giải thích. Tìm thêm các bài viết về công thức thống kê và các hàm liên quan trong Excel tại đây. Nếu bạn thích blog của chúng tôi, hãy chia sẻ nó với bạn bè của bạn trên Facebook. Và bạn cũng có thể theo dõi chúng tôi trên Twitter và Facebook. Chúng tôi rất muốn nghe ý kiến của bạn, hãy cho chúng tôi biết cách chúng tôi có thể cải thiện, bổ sung hoặc đổi mới công việc của mình và làm cho nó tốt hơn cho bạn. Viết thư cho chúng tôi tại [email protected].