Cách sử dụng hàm HYPGEOM.DIST trong Excel
Trong bài viết này, chúng ta sẽ tìm hiểu Cách sử dụng hàm HYPGEOM.DIST trong Excel.
Phân phối siêu phương là gì?
Phân phối siêu đại là một phân phối xác suất rời rạc mô tả xác suất của k thành công trong một mẫu mà không có sự thay thế từ một tập hợp hữu hạn. Ví dụ vẽ 4 quả bóng từ một túi 20 quả bóng có 8 quả bóng trắng và 12 quả bóng đen. Xác suất để rút ra đúng 1 bi trắng trong số 4 bi rút ra mà không thay thế là bao nhiêu. Chắc hẳn bạn đang nghĩ câu hỏi này khác với hàm phân phối chuẩn như thế nào. Sự cố xảy ra đối với điều kiện không có thay thế. Khi chúng ta thay quả bóng đã rút ra, xác suất của quả bóng được rút ra vẫn giữ nguyên cho mỗi sự kiện trong khi nếu chúng ta không thay quả bóng, xác suất bóng thay đổi trong túi cho mỗi lần rút. Về mặt toán học, chúng ta có một công thức để tính xác suất cho những trường hợp như vậy.
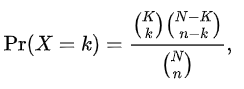
Đây:
N là quy mô dân số, K là số trạng thái thành công trong quần thể, n là số lần rút thăm (tức là số lần rút ra trong mỗi lần thử nghiệm), k là số lần thành công được quan sát, () là hàm tổ hợp được biểu thị bằng n! / (k! (n-k)!) (đây! * là hàm giai thừa)
Điều này vẫn rất phức tạp để sử dụng trong Excel. Đối với điều này, Excel cung cấp hàm HYPGEOM.DIST được tích hợp sẵn để tính toán giá trị xác suất trong phân phối hình học mà không cần thay thế.
Hàm HYPGEOM.DIST trong Excel
HYPGEOM.DIST lấy 4 đối số số và 1 giá trị boolean để xác định loại hàm xác suất (cdf hoặc pdf). Chúng ta hãy hiểu từng lập luận này được liệt kê dưới đây.
HYPGEOM.DIST Cú pháp hàm:
|
=HYPGEOM.DIST ( sample_s , number_sample , population_s , number_pop , cumulative) |
sample_s: số lần thành công trong số mẫu_sample: kích thước mẫu được vẽ ra quần thể_s: số lần thành công trong số tổng thể_pop: quy mô tổng thể tích lũy *: giá trị logic xác định dạng của hàm.
Nếu tích lũy là TRUE, hàm HYPGEOM.DIST trả về hàm phân phối tích lũy; nếu FALSE, nó trả về hàm mật độ xác suất.
Ví dụ:
Tất cả những điều này có thể khó hiểu. Hãy hiểu cách sử dụng hàm bằng một ví dụ. Ở đây chúng ta lấy một bộ bài thông thường và chúng ta rút 4 lá từ bộ bài mà không cần thay thế. Xác suất nhận được chính xác * 1 thẻ câu lạc bộ trong 4 thẻ rút ra là bao nhiêu?
Hãy sử dụng công thức dưới đây để có được xác suất cần thiết.
Sử dụng công thức:
|
=HYPGEOM.DIST( B3, B4, B5, B6, TRUE) |
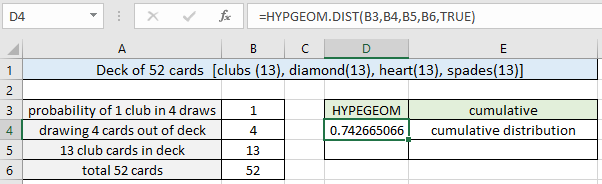
Như bạn có thể thấy, xác suất 0,74 hoặc 74% (xấp xỉ) nhận được chính xác 1 thẻ câu lạc bộ khi rút 4 thẻ mà không cần thay thế. Bây giờ chúng ta có thể tính toán xác suất để rút được ít nhất * 1 thẻ câu lạc bộ cho các thông số giống nhau chỉ bằng cách thay đổi đối số tích lũy trong hàm hiển thị bên dưới.
Sử dụng công thức:
|
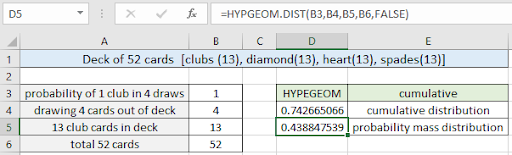
=HYPGEOM.DIST( B3, B4, B5, B6, FALSE) |
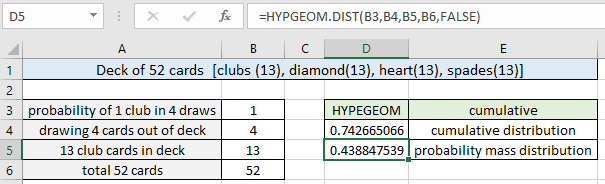
Như bạn có thể thấy, xác suất nhận được ít nhất * 1 thẻ câu lạc bộ là 0,44 hoặc 44% (xấp xỉ) khi rút 4 thẻ mà không cần thay thế. Bạn có thể sử dụng hàm BINOM.DIST, nếu các thẻ đã rút được thay thế trở lại vì hàm BINOM.DIST hoạt động với điều kiện các xác suất phải được duy trì cho các thẻ đã rút.
Đây là tất cả các ghi chú quan sát bằng cách sử dụng hàm HYPGEOM.DIST trong Excel
Ghi chú:
-
Hàm chỉ hoạt động với các số. Nếu bất kỳ đối số nào khác với tích lũy không phải là số, hàm trả về lỗi #VALUE! lỗi.
-
Hàm trả về giá trị lỗi #NUM! Lỗi.
-
Nếu giá trị sample_s <0 hoặc giá trị sample_s> number_sample.
-
Nếu giá trị mẫu_số> giá trị quần thể_s.
-
Nếu giá trị sample_s> (number_sample – number_pop + folk_s)
-
giá trị.
-
Nếu Number_sample giá trị? 0 hoặc Number_sample> number_pop.
-
Nếu giá trị của quần thể? 0 hoặc dân số> number_pop.
-
Nếu number_pop? 0. Đối số tích lũy có thể được sử dụng với các số boolean (0 và 1) hoặc (FALSE hoặc TRUE).
-
Giá trị ở dạng thập phân hoặc giá trị tính bằng phần trăm là cùng một giá trị trong Excel.
-
Chuyển đổi giá trị thành tỷ lệ phần trăm, nếu cần.
-
Bạn có thể cung cấp trực tiếp các đối số cho hàm hoặc sử dụng tham chiếu ô như được giải thích trong ví dụ.
Hy vọng bài viết này về Cách sử dụng hàm HYPGEOM.DIST trong Excel là giải thích. Tìm thêm các bài viết về công thức thống kê và các hàm liên quan trong Excel tại đây. Nếu bạn thích blog của chúng tôi, hãy chia sẻ nó với bạn bè của bạn trên Facebook. Và bạn cũng có thể theo dõi chúng tôi trên Twitter và Facebook. Chúng tôi rất muốn nghe ý kiến của bạn, hãy cho chúng tôi biết cách chúng tôi có thể cải thiện, bổ sung hoặc đổi mới công việc của mình và làm cho nó tốt hơn cho bạn. Viết thư cho chúng tôi tại [email protected].