Cách sử dụng hàm NORM.S.DIST trong Excel
Trong bài này, chúng ta sẽ học Cách sử dụng hàm NORM.S.DIST trong Excel.
Phân phối tích lũy bình thường là gì?
Phân phối tích lũy bình thường là một loại phân phối xác suất liên tục cho một biến ngẫu nhiên có giá trị thực. Dạng tổng quát của hàm mật độ xác suất của nó được đưa ra bởi:
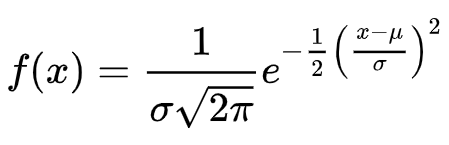
Phân phối tích lũy chuẩn chuẩn là một trường hợp đặc biệt của phân phối tích lũy chuẩn với giá trị trung bình () = 0 và độ lệch chuẩn () = 1. Dạng tổng quát của phân phối tích lũy chuẩn chuẩn được đưa ra bởi:
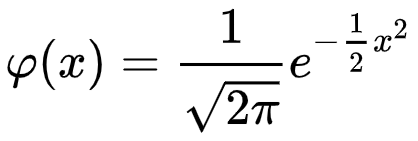
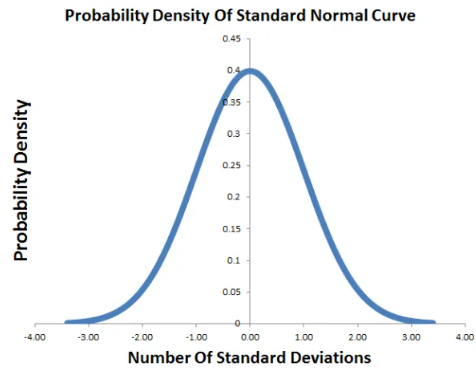
Đồ thị của đường cong phân phối chuẩn Chuẩn
Phân phối chuẩn chuẩn có giá trị trung bình bằng 0 và độ lệch chuẩn là một. Vì vậy, đường cong mật độ xác suất so với độ lệch chuẩn cho phân phối tích lũy chuẩn chuẩn được hiển thị bên dưới.
Công thức toán học nêu trên rất phức tạp để nhập công thức khôn ngoan, vì vậy excel đã đưa ra công thức mặc định. Bây giờ chúng ta hãy học cách tính xác suất chuẩn thông thường cho phân phối tích lũy hoặc phân phối khối lượng xác suất bằng cách sử dụng hàm NORM.S.DIST trong Excel.
Hàm NORM.S.DIST trong Excel
Hàm thực hiện tương tự như công thức toán học. Hàm nhận giá trị x hoặc z làm đối số và đối số tích lũy xác định loại kết quả pdf hoặc cdf. Hãy hiểu thêm về các đối số bên dưới
NORM.S.DIST Cú pháp hàm:
|
=NORM.S.DIST(x,cumulative) |
x: giá trị mà bạn muốn phân phối tích lũy: giá trị lôgic xác định dạng của hàm. Nếu tích lũy là TRUE, NORM.S.DIST trả về hàm phân phối tích lũy; nếu FALSE, nó trả về hàm khối lượng xác suất.
Ví dụ:
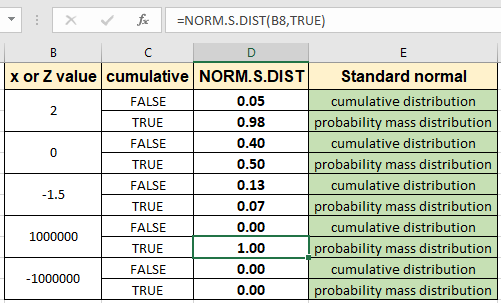
Tất cả những điều này có thể khó hiểu. Hãy hiểu cách sử dụng hàm bằng một ví dụ. Ở đây chúng tôi lấy một số giá trị x và tìm hiểu các kiểu phân phối khác nhau. Đầu tiên chúng ta sẽ đánh giá phân phối tích lũy có giá trị z là 2 đối với phân phối chuẩn chuẩn có giá trị trung bình mặc định = 0 và độ lệch chuẩn = 1
Sử dụng công thức:
|
=NORM.S.DIST(B2, FALSE) |
Hoặc
|
=NORM.S.DIST(B2, 0) |
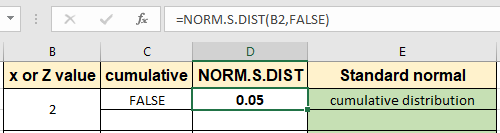
Giá trị xác suất tương ứng với 2 là 0,05 cho tập dữ liệu phân phối chuẩn chuẩn. Bây giờ trích xuất xác suất cho phân phối khối lượng xác suất cho cùng một giá trị z như hình dưới đây.
Sử dụng công thức:
|
=NORM.S.DIST(B2, TRUE) |
Hoặc
|
=NORM.S.DIST(B2, 1) |
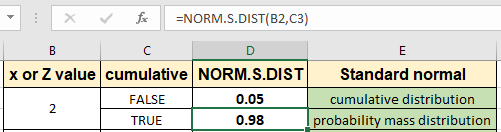
Như bạn có thể thấy xác suất cho điều này cao hơn nhiều so với giá trị trước đó. Bạn có thể kiểm tra cả hai giá trị cho các giá trị z khác nhau. Chỉ cần sao chép công thức sang các ô khác bằng tổ hợp phím tắt Ctrl + D hoặc kéo xuống từ dưới cùng bên phải của ô.
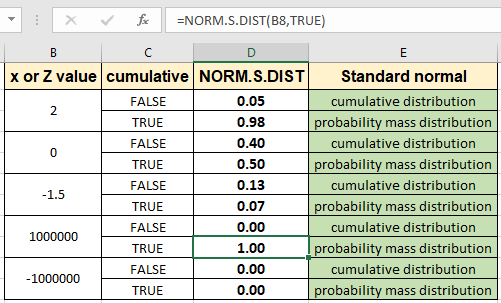
Như bạn có thể thấy sự khác biệt về kết quả như trong hình trên.
Bạn nhận thấy rằng excel dễ dàng tạo ra công thức phức tạp cho bạn như thế nào. Bạn có thể nhận được kết quả tương tự bằng cách sử dụng hàm NORM.DIST với việc đặt giá trị trung bình = 0 và độ lệch chuẩn = 1. Bạn cũng có thể tìm thấy nghịch đảo của phân phối tích lũy chuẩn chuẩn bằng cách sử dụng hàm NORM.S.INV.
Dưới đây là tất cả các ghi chú quan sát bằng cách sử dụng hàm NORM.S.DIST trong Excel
Ghi chú:
-
Hàm chỉ hoạt động với giá trị z là số. Mọi giá trị không phải là số sẽ dẫn đến lỗi #VALUE! lỗi.
-
Hàm có thể nhận các giá trị boolean 0 và 1 hoặc sử dụng các giá trị boolean TRUE và FALSE để chuyển sang phân phối tích lũy và phân phối khối lượng xác suất.
-
Giá trị Z hoặc x có thể được cung cấp trực tiếp hoặc sử dụng tham chiếu ô như được hiển thị trong ví dụ trên.
Hy vọng bài viết này về Cách sử dụng hàm NORM.S.DIST trong Excel là giải thích. Tìm thêm các bài viết về công thức thống kê và các hàm liên quan trong Excel tại đây. Nếu bạn thích blog của chúng tôi, hãy chia sẻ nó với bạn bè của bạn trên Facebook. Và bạn cũng có thể theo dõi chúng tôi trên Twitter và Facebook. Chúng tôi rất muốn nghe ý kiến của bạn, hãy cho chúng tôi biết cách chúng tôi có thể cải thiện, bổ sung hoặc đổi mới công việc của mình và làm cho nó tốt hơn cho bạn. Viết thư cho chúng tôi tại [email protected].