Cách sử dụng hàm Z.TEST trong Excel
Trong bài viết này, chúng ta sẽ tìm hiểu Cách sử dụng hàm Z.TEST trong Excel.
Kiểm tra giả thuyết là gì và cách sử dụng Z -Test để kiểm tra giả thuyết? Trong thống kê, kiểm định Giả thuyết được sử dụng để tìm ước tính giá trị trung bình cho tập dữ liệu dân số bằng cách sử dụng hàm phân phối khác nhau dựa trên một phần của tập dữ liệu dân số có tên là tập dữ liệu mẫu. Giả thuyết thống kê, đôi khi được gọi là phân tích dữ liệu xác nhận, là một giả thuyết có thể kiểm tra được trên cơ sở quan sát một quá trình được mô hình hóa thông qua một tập hợp các biến ngẫu nhiên. Có hai loại giả thuyết. Một là giả thuyết vô hiệu là tuyên bố đã được khẳng định và giả thuyết khác là giả thuyết thay thế đối lập với giả thuyết không. Ví dụ: nếu chúng ta nói giới hạn tối đa dẫn đến một gói maggi không được vượt quá 225 ppm (phần triệu) và ai đó tuyên bố rằng có nhiều hơn giới hạn cố định so với giả thuyết rỗng (được ký hiệu là U ~ 0 ~) và giả thuyết thay thế (được ký hiệu là bởi U ~ a ~)
U ~ 0 ~ = hàm lượng chì trong gói maggi lớn hơn hoặc bằng 225ppm. U ~ a ~ = hàm lượng chì trong gói maggi nhỏ hơn 225 ppm.
Vì vậy, giả thuyết trên là một ví dụ về kiểm định bên phải vì tình huống cơ bản nằm ở phía bên phải của đường cong phân phối.
Nếu tình huống cơ bản nằm ở phía bên trái thì nó sẽ được gọi là bài kiểm tra bên trái. Hãy lấy thêm một ví dụ minh họa bài kiểm tra một phía. Ví dụ, nếu selina cho biết trung bình cô ấy có thể chống đẩy 60 lần. Bây giờ bạn có thể nghi ngờ tuyên bố đó và cố gắng giả thuyết tình huống trong thuật ngữ thống kê sau đó, giả thuyết rỗng và giả thuyết thay thế được nêu bên dưới U ~ 0 ~ = selina có thể thực hiện 60 lần đẩy U ~ a ~ = selina không thể thực hiện 60 lần đẩy Đây là một trong hai -kết thúc kiểm tra trong đó tình huống cơ bản nằm ở cả hai bên của tuyên bố được yêu cầu. Các bài kiểm tra theo đuôi này ảnh hưởng đến kết quả của thống kê. Vì vậy, hãy chọn giả thuyết rỗng và giả thuyết thay thế một cách cẩn thận.
Kiểm định Z – Kiểm định Z là bất kỳ kiểm định thống kê nào mà phân phối của thống kê kiểm định theo giả thuyết rỗng có thể được xấp xỉ bằng phân phối chuẩn. Kiểm tra Z kiểm tra giá trị trung bình của một phân phối mà chúng ta đã biết phương sai tổng thể. Do định lý giới hạn trung tâm, nhiều thống kê thử nghiệm được phân phối gần đúng chuẩn cho các mẫu lớn. Thống kê thử nghiệm được giả định là có phân phối chuẩn, chẳng hạn như độ lệch chuẩn phải được biết để thực hiện phép thử z chính xác. Ví dụ, một nhà đầu tư muốn kiểm tra xem liệu lợi nhuận trung bình hàng ngày của một cổ phiếu có lớn hơn 1% hay không có thể được đánh giá bằng cách sử dụng Z test. Thống kê Z hoặc Z-score * là một số thể hiện có bao nhiêu độ lệch chuẩn trên hoặc dưới tổng thể trung bình mà điểm thu được từ kiểm tra Z là bao nhiêu. Về mặt toán học, đầu tiên chúng ta quyết định giả thuyết rỗng và tính điểm Z cho phân phối bằng công thức.
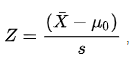
Ở đây X (với một thanh) là giá trị trung bình của mảng mẫu U ~ 0 ~ là giá trị trung bình của tổng thể ước tính s là độ lệch chuẩn trong đó s bằng std / (n) ^ 1/2 ^ (với n là cỡ mẫu) .
Như đã nêu ở trên Z – kiểm tra tuân theo phân phối chuẩn chuẩn. Vì vậy, về mặt toán học trong Excel, nó tuân theo công thức sau.
Z.TEST (array, x, sigma) = 1- Norm.S.Dist ((Average (array) – x) / (sigma / (n) ^ 1/2 ^), TRUE)
hoặc khi sigma bị bỏ qua:
Z.TEST (mảng, x) = 1- Norm.S.Dist ((Trung bình (mảng) – x) / (STDEV (mảng) / (n) ^ 1/2 ^), TRUE)
trong đó x là AVERAGE trung bình mẫu (mảng) và n là COUNT (mảng).
Hãy cùng tìm hiểu cách thực hiện kiểm tra Z bằng cách sử dụng hàm Z.TEST để tính toán mối quan hệ giữa hai tập dữ liệu đã cho (thực tế và quan sát).
Hàm Z.TEST trong Excel
Hàm Z.TEST trả về xác suất giá trị trung bình của mẫu sẽ lớn hơn giá trị trung bình của các quan sát trong tập dữ liệu (mảng). Hàm nhận các đối số sau đây.
Z.TEST Cú pháp hàm cho xác suất một phía:
|
=Z.TEST ( array , x , [sigma] ) |
Hàm cũng có thể được sử dụng để tính xác suất hai phía.
Z.TEST Cú pháp hàm cho xác suất một phía:
|
=2 * MIN(Z.TEST ( array , x , [sigma] ), 1-Z.TEST ( array , x , [sigma] ) ) |
mảng: phân phối dữ liệu mẫu x: giá trị mà phép thử z được đánh giá [sigma] *: [tùy chọn] Độ lệch chuẩn tổng thể (đã biết). Nếu bỏ qua, độ lệch chuẩn mẫu sẽ được sử dụng.
Ví dụ:
Tất cả những điều này có thể khó hiểu. Hãy hiểu cách sử dụng hàm bằng một ví dụ. Ở đây chúng ta có một tập dữ liệu mẫu Bán hàng và chúng ta cần tìm xác suất thử nghiệm Z cho tổng thể giả thuyết đã cho có nghĩa là giả sử một thử nghiệm theo đuôi.
Sử dụng công thức:
|
= Z.TEST( A2:A9 , C3 ) |
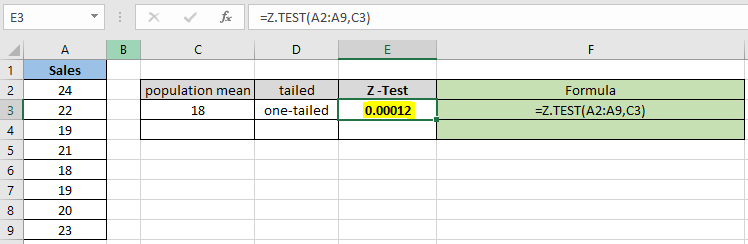
Giá trị xác suất ở dạng thập phân, vì vậy bạn có thể chuyển đổi giá trị thành phần trăm thay đổi định dạng của ô thành phần trăm.
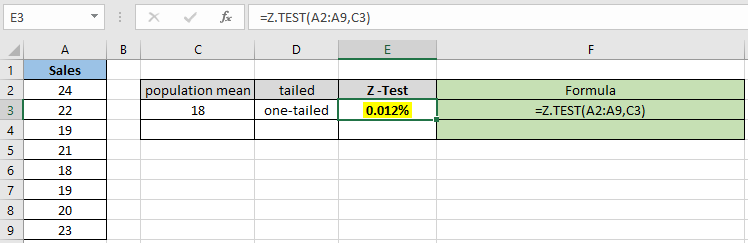
Như bạn có thể thấy giá trị xác suất cho tổng thể giả thuyết có nghĩa là 18 là 0,012% cho phân phối một phía. Bây giờ hãy tính xác suất giả sử hai phân phối theo sau có cùng tham số.
Sử dụng công thức:
|
= 2 * MIN( Z.TEST(A2:A9,C4) , 1 – Z.TEST(A2:A9,C4) ) |
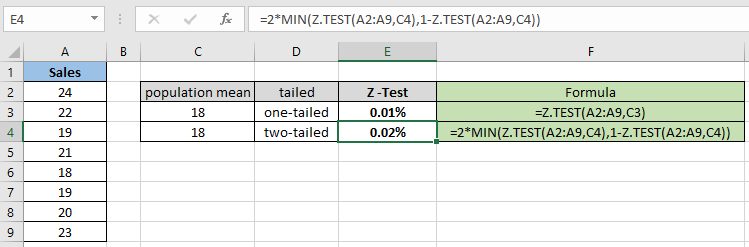
Đối với phân phối hai phía, xác suất sẽ tăng gấp đôi cho cùng một tập dữ liệu mẫu. Vì vậy, cần kiểm tra giả thuyết vô hiệu và giả thuyết thay thế. Bây giờ hãy tính xác suất cho giá trị trung bình của tổng thể được giả thuyết khác nhau và một phân phối theo đuôi.
Sử dụng công thức:
|
= Z.TEST( A2:A9 , C5 ) |
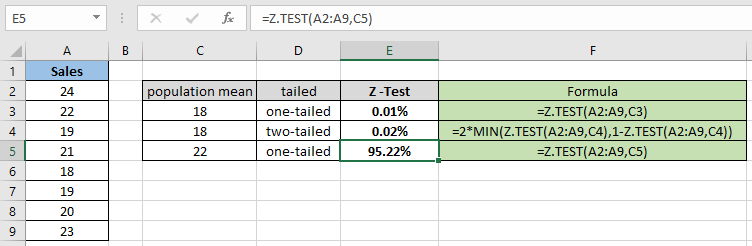
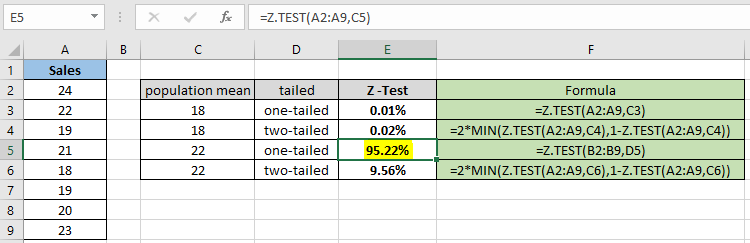
Như bạn có thể thấy giá trị xác suất cho tổng thể giả thuyết có nghĩa là 22 là 95,22% cho phân phối một phía. Bây giờ hãy tính xác suất giả sử hai phân phối theo sau có cùng tham số.
Sử dụng công thức:
|
= 2 * MIN( Z.TEST(A2:A9,C6) , 1 – Z.TEST(A2:A9,C6) ) |
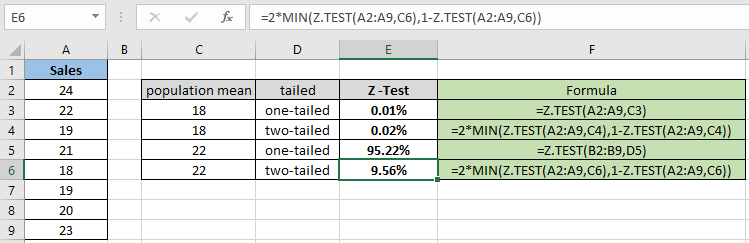
Như bạn có thể khác với ảnh chụp nhanh ở trên rằng giá trị xác suất nhận được ít hơn khi tính toán phân phối hai phía. Hàm trả về 9,56% cho trung bình dân số được giả thuyết là 22.
Z.TEST đại diện cho xác suất mà giá trị trung bình của mẫu sẽ lớn hơn giá trị quan sát được AVERAGE (mảng), khi giá trị trung bình của tổng thể cơ bản là 0. Từ tính đối xứng của phân phối Chuẩn, nếu AVERAGE (mảng) <x, Z.TEST sẽ trả về giá trị lớn hơn 0,5.
Đây là tất cả các ghi chú quan sát bằng cách sử dụng hàm Z.TEST trong Excel
Ghi chú:
-
Hàm chỉ hoạt động với các số. Nếu trung bình dân số hoặc đối số sigma không phải là số, hàm trả về lỗi #VALUE! lỗi.
-
Giá trị ở dạng thập phân hoặc giá trị tính bằng phần trăm là cùng một giá trị trong Excel.
Chuyển đổi giá trị thành tỷ lệ phần trăm, nếu cần.
-
Hàm trả về giá trị lỗi #NUM! Lỗi, nếu đối số sigma là 0.
-
Hàm trả về # N / A! Lỗi nếu mảng được cung cấp trống.
-
Hàm trả về # DIV / 0! Lỗi, .. Nếu độ lệch chuẩn của mảng là 0 và đối số sigma bị bỏ qua.
-
Nếu mảng chỉ chứa một giá trị.
-
Hy vọng bài viết này về Cách sử dụng hàm Z.TEST trong Excel là giải thích. Tìm thêm các bài viết về công thức thống kê và các hàm liên quan trong Excel tại đây. Nếu bạn thích blog của chúng tôi, hãy chia sẻ nó với bạn bè của bạn trên Facebook. Và bạn cũng có thể theo dõi chúng tôi trên Twitter và Facebook. Chúng tôi rất muốn nghe ý kiến của bạn, hãy cho chúng tôi biết cách chúng tôi có thể cải thiện, bổ sung hoặc đổi mới công việc của mình và làm cho nó tốt hơn cho bạn. Viết thư cho chúng tôi tại [email protected].