在Excel分配问题

该模型中，我们要解决的外观在Excel如下。

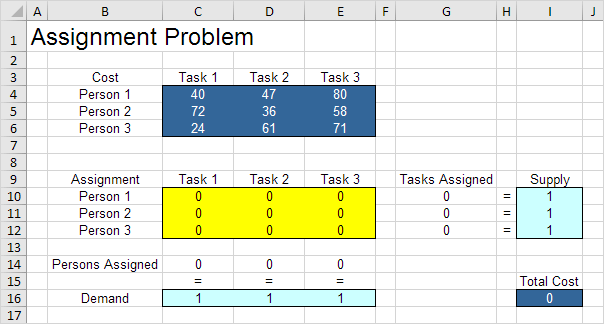
1.要制定这个分配问题，回答以下三个问题。

\一种。什么是要做出的决定？对于这个问题，我们需要Excel来找出分配给它的任务（是= 1，否= 0）的人。例如，如果我们指定的人1任务1，小区C10等于1。如果没有，C10单元格等于0

\湾什么是对这些决定的约束？每个人只能做一个任务（供应= 1）。每个任务只需要一个人（需求= 1）。

\C。什么是对这些决定整体性能的措施？性能的综合指标是分配的总成本，所以目标是尽量减少这一数量。

2.为了使模型更容易理解，命名以下范围。

3.将以下功能。

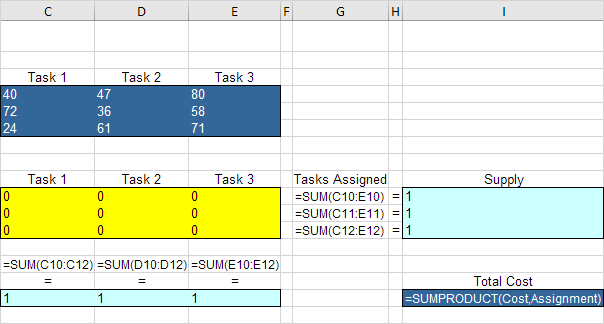
说明：SUM函数计算分配给一个人，分配给任务的人数任务的数量。总成本等于成本和分配的SUMPRODUCT。

有了这个配方，就很容易分析任何审判的解决方案。

例如，如果我们指定的人1任务1，第2个人到任务2和3人到任务3，已分配的任务等于供应和人员分配平等的需求。该方案具有147总成本

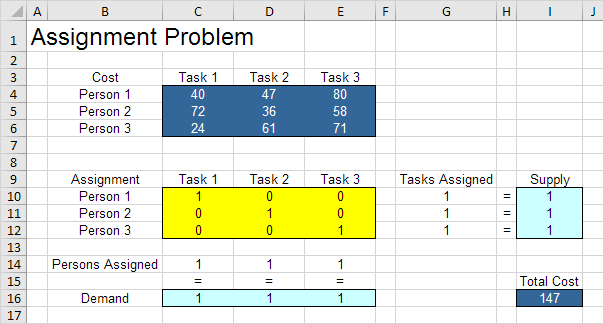
这是没有必要使用试验和错误。接下来我们将描述Excel求解如何可以用来快速地找到最佳的解决方案。

为了找到最佳的解决方案，执行下列步骤。

1.在数据选项卡，在分析组中，单击求解。

注：找不到求解器按钮？点击此处加载规划求解加载项。

进入求解器参数（读）。结果应与下面的图片一致。

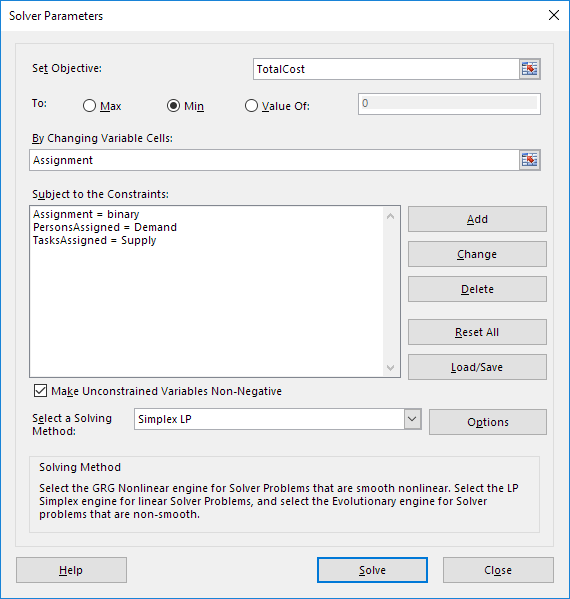
你必须键入区域名称或点击电子表格中的单元格的选择。

2.客观输入TOTALCOST。

3.单击最小。

4.对于改变可变细胞进入分配。

5.单击添加到输入下列约束。

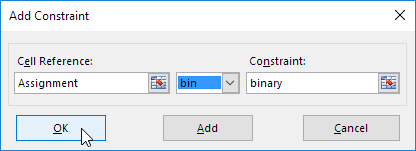
注：二元变量是0或1

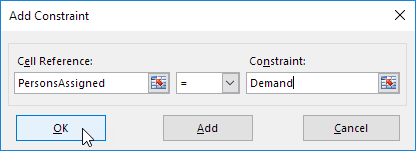
6.单击添加到输入下面的约束。

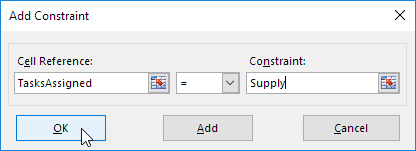
7.单击添加到输入下面的约束。

8.检查“使无约束变量非负”，然后选择“单面LP”。

9.最后，单击解决。

结果：

最佳的解决方案：

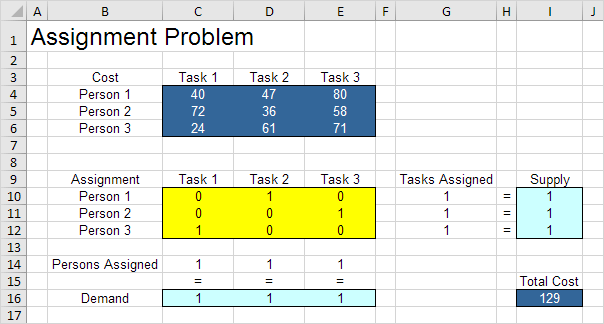
结论：它是最佳的人1分配到任务2，人2〜任务3和Person 3至任务1.该溶液给出129.最小成本

所有的约束都满足。