盒须图在Excel
简单箱须图| 链接:#outliers [离群]| 链接:#箱线图,计算[箱线图计算]
四分位数,中位数,第三个四分位和一个数据集的最大值。
简单的盒子须图
1.例如,选择范围A1:A7。
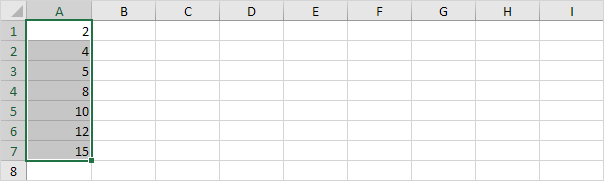
注意:您不必从最小到最大的数据点进行排序,但它会帮助你了解箱须图。
2.在插入选项卡,在图表组中,单击统计信息图表符号。

3.单击箱线。
结果:
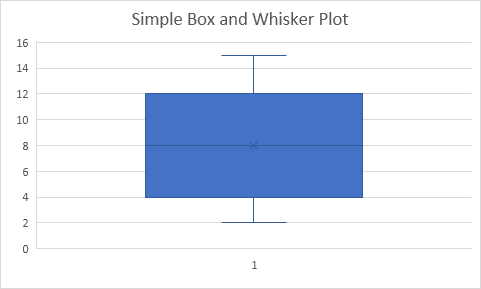
说明:盒的中间的线表示中值或中间数(8)。在框中的x表示平均值(也8在本例中)。中位数分割数据集到一个下半部\ {2,4,5}和顶半\ {10,12,15}。所述箱的底部的线表示的下半部或第一四分位(4)的中值。箱的顶部线表示上半部分或第三四分位数(12)的中值。晶须(垂直线)从盒子的最小值(2)和最大值(15)的端部延伸。
离群值
1.例如,选择范围A1:A11。
注意:中值或中间数(8)将所述的数据集分为两半:\ {1,2,2,4,5}和\ {10,12,15,18,35}。的第一四分位数(Q〜1〜)是上半场的中值。 Q〜1〜= 2。第三四分位数(Q〜3〜)是第二半的中值。 Q〜3〜= 15
2.在插入选项卡,在图表组中,单击统计信息图表符号。

3.单击箱线。

结果:
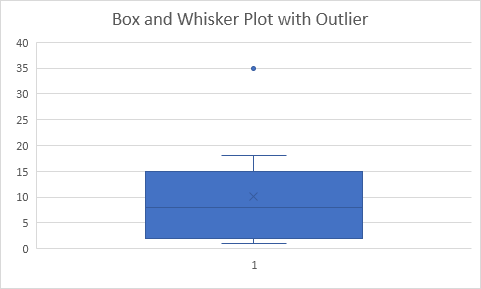
说明:四分位距(IQR)被定义为第一四分位和第三个四分位数之间的距离。在这个例子中,IQR = Q〜3〜 – Q〜1〜= 15 – 2 = 13,如果超过第一四分位数以下IQR 1.5倍的距离(Q〜1〜的数据点被认为是异常值 – 1.5 IQR = 2 – 1.5 13 = -17.5)或第三四分位数以上1.5倍IQR(Q〜3〜+ 1.5 IQR = 15 + 1.5 13 = 34.5)。因此,在这个例子中,35被认为是异常值。其结果是,顶晶须延伸到该范围内的最大值(18)。
4.更改最后一个数据点到34
结果:
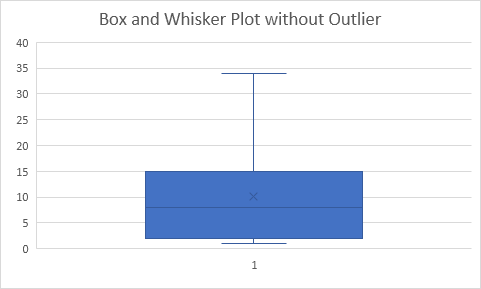
说明:所有的数据点是-17.5和34.5之间。其结果是,该晶须延伸到最小值(2)和最大值(34)。
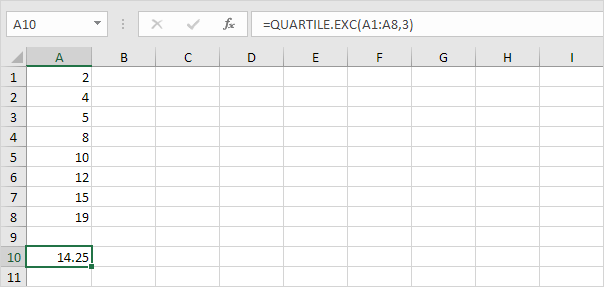
箱线图计算
在大多数情况下,你可以不能轻易确定第一个四分位和第三个四分位数,而不进行计算。
1.例如,选择下面的数据点的偶数。
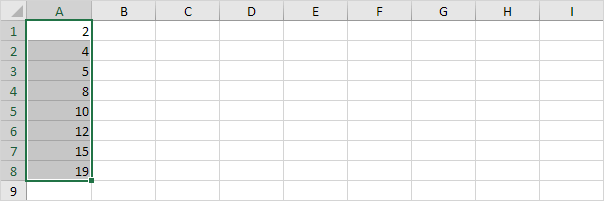
2.在插入选项卡,在图表组中,单击统计信息图表符号。

3.单击箱线。

结果:
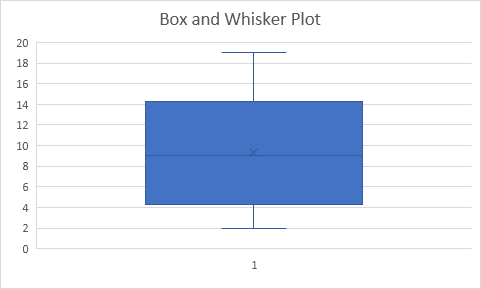
说明:Excel使用QUARTILE.EXC函数来计算第一四分位(Q〜1〜),第二四分位(Q〜2〜或中值)和第三四分位数(Q〜3〜)。
两个值之间的插值函数来计算四分位数。
在该示例中,n = 8(个数据点)。
-
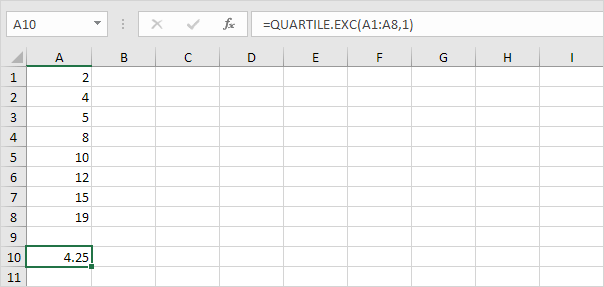
Q〜1〜= 1/4(N + 1)个值= 1/4(8 + 1)个值= 2 1 /第四值= 4 + 1/4(5-4)= 4 1/4 。您可以通过使用QUARTILE.EXC功能或寻找在票房须图证实这一数字。
-
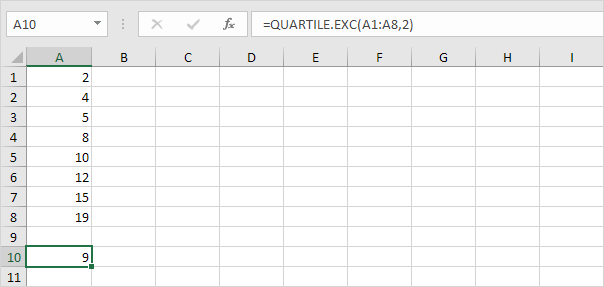
Q〜2〜= 1/2(N + 1)个值= 1/2(8 + 1)个值= 4 1 /二路值= 8 + 1/2(10-8)= 9。这使得某种意义上说,中位数是平均中间的两个数字。
-
Q〜3〜= 3/4(N + 1)个值= 3/4(8 + 1)个值= 6 3 /第四值= 12 + 3/4 *(15-12)= 14 1 / 4。同样,你可以通过使用QUARTILE.EXC功能或寻找在票房须图证实这一数字。