回归分析在Excel
R广场| 链接:#意义-F-和p值[意义F和P值]| 链接:#coefficients [系数]| 链接:#residuals [残差]
这个例子教你如何在Excel中运行的线性回归分析和如何解释摘要输出。
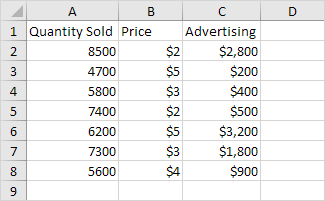
下面你可以找到我们的数据。最大的问题是:有没有售出数量(输出),价格和广告(输入)之间的关系。换句话说:我们可以预测售出数量,如果我们知道价格和广告?
1.在数据选项卡,在分析组中,单击数据分析。
注:找不到数据分析按钮?点击这里载入分析工具库加载项。
2.选择回归,然后单击确定。
3.选择Y范围(A1:A8)。这是预测变量(也称为从属变量)。
4.选择X范围(B1:C8)。这些解释变量(也称为自变量)。这些列必须是彼此相邻的。
5.检查标签。
6.单击输出范围框,然后选择单元格A11。
7.检查残差。
8.单击确定。
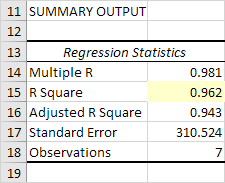
Excel中产生以下摘要输出(四舍五入至小数点后3位)。
R平方
R平方等于0.962,这是一个非常不错的选择。在售出数量变化的96%是由自变量的价格和广告解释。越接近1,更好的回归线(读取)适合的数据。
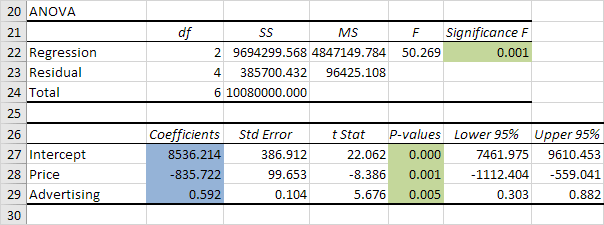
意义F和P值
要检查你的结果是可靠的(统计上显著),看看意义F(0.001)。如果该值小于0.05时,你真行。
如果意义F是大于0.05,它可能会更好,停止使用该组自变量。删除具有高P值(大于0.05)的变量并重新运行回归直到意义时会降低低于0.05。
大部分或全部的P值应低于0.05以下。在我们的例子是这种情况。 (0.000,0.001和0.005)。
系数
回归线为:y =售出数量= 8536.214 -835.722价格+ 0.592广告。换句话说,对于每个价格单位增加,售出数量与835.722单位减小。对于广告的每个单位增加,售出数量增加与0.592单位。这是有价值的信息。
您也可以使用这些系数来做预测。例如,如果价格等于$ 4和广告等于$ 3000,你也许能达到销售的8536.214 -835.722 4 + 0.592 = 3000一6970.数量
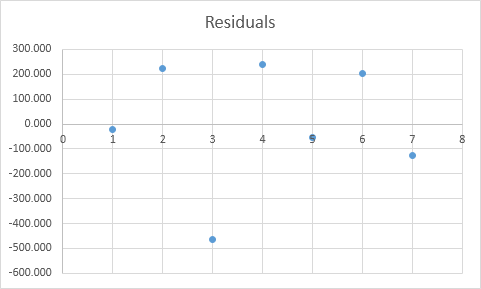
残差
残差为您显示实际数据点有多远是FOM的预测数据点(使用公式)。例如,第一个数据点等于8500使用方程,预测数据点等于8536.214 -835.722 2 + 0.592 2800 = 8523.009,给人一种残留的8500 – 8523.009 = -23.009。
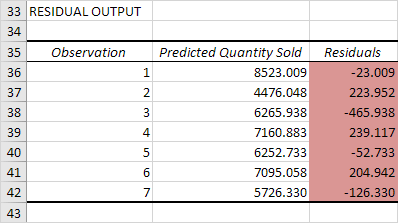
您还可以创建这些残差的散点图。