在Excel中最短路径问题
制订型号| 链接:#试错误[试用和错误]| 链接:#解决模型[求解模型]
使用解算器在Excel中找到一个无向网络从节点S到节点T的最短路径。在网络中的点被称为节点(S,A,B,C,d,E和T)。在网络中的线被称为弧(SA,SB,SC,AC等)。
制定示范
该模型中,我们要解决的外观在Excel如下。
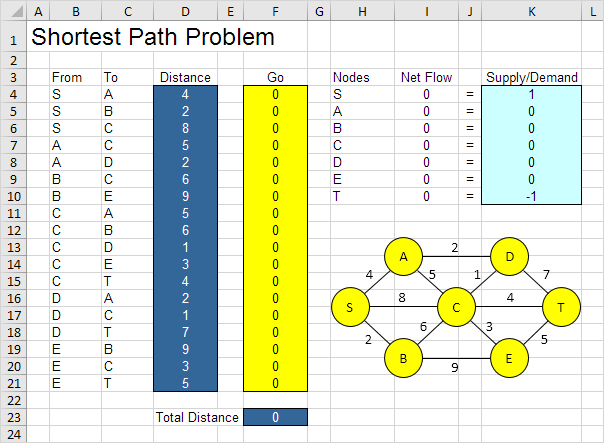
1.要制定这条最短路径问题,回答以下三个问题。
\一种。什么是要做出的决定?对于这个问题,我们需要Excel来看看一个弧线的最短路径上或不(是= 1,否= 0)。例如,如果SB是最短的路径的一部分,小区F5等于1。如果不是,小区F5等于0
\湾什么是对这些决定的约束?净流量(流出 – 流在)每个节点的应等于供应/需求。节点S应该只有一个传出弧(净流量= 1)。节点T应该只有一个迁入弧(净流量= -1)。所有其他节点应具有一个传出弧和一个轧前弧如果节点是最短路径(净流量= 0)或无流量(净流量= 0)上。
\C。什么是对这些决定整体性能的措施?的整体性能度量是最短路径的总距离,所以目标是最小化这个量。
2.为了使模型更容易理解,命名以下范围。
|
Range Name |
Cells |
|
From |
B4:B21 |
|
To |
C4:C21 |
|
Distance |
D4:D21 |
|
Go |
F4:F21 |
|
NetFlow |
I4:I10 |
|
SupplyDemand |
K4:K10 |
|
TotalDistance |
F23 |
3.将以下功能。
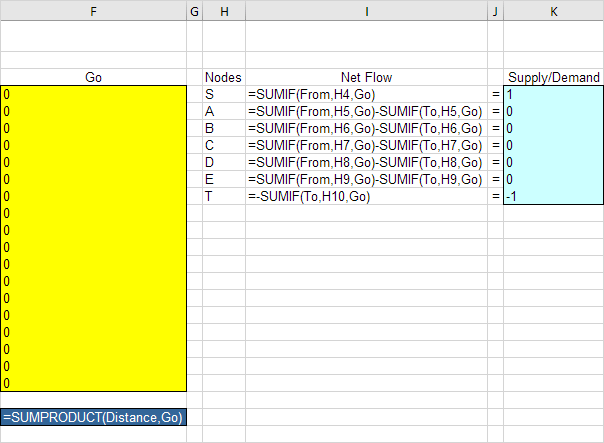
SUMIF函数计算每个节点的净流量。对于节点S,该SUMIF函数求和在转到列中的值与“S”,在从塔。其结果是,只有细胞F4,F5或F6可以是1(一传出弧)。对于节点T,则SUMIF函数求和在转到列中的值与“T”的列中。其结果是,只有小区F15,F18或F21可以是1(一个轧前弧)。对于所有其他节点,Excel探讨在从和到列。总距离等于距离和围棋的SUMPRODUCT。
试错
有了这个配方,就很容易分析任何审判的解决方案。
1.例如,路径SBET具有16的总距离
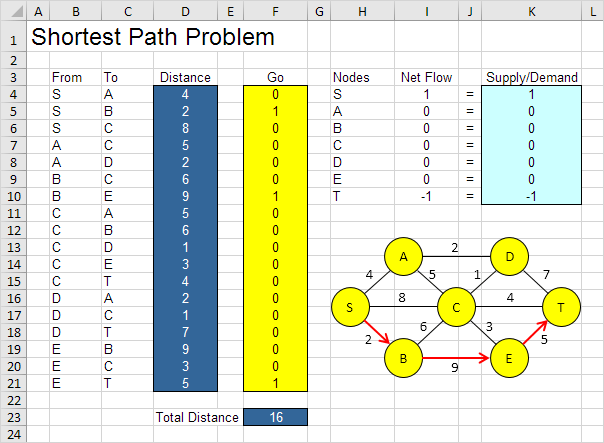
这是没有必要使用试验和错误。接下来我们将描述Excel求解如何可以用来快速地找到最佳的解决方案。
求解该模型
为了找到最佳的解决方案,执行下列步骤。
1.在数据选项卡,在分析组中,单击求解。
注:找不到求解器按钮?点击此处加载规划求解加载项。
进入求解器参数(读)。结果应与下面的图片一致。
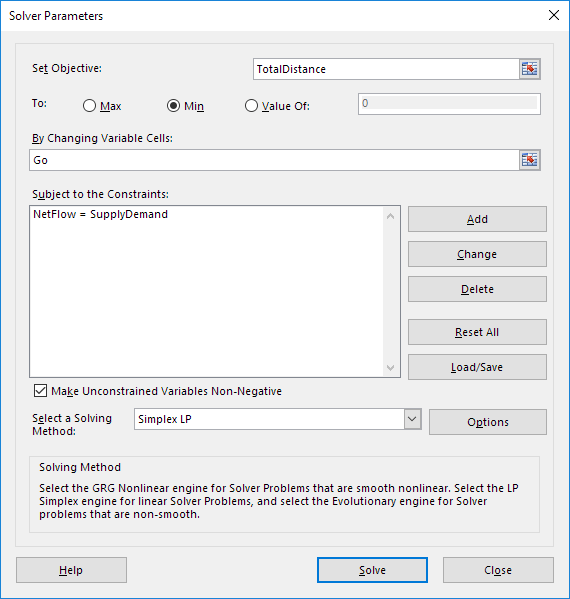
你必须键入区域名称或点击电子表格中的单元格的选择。
2.客观输入TotalDistance。
3.单击最小。
4.对于改变可变单元格中输入搜索。
5.单击添加到输入下列约束。
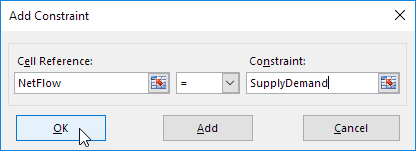
6.检查“使无约束变量非负”,然后选择“单面LP”。
7.最后,单击解决。
结果:
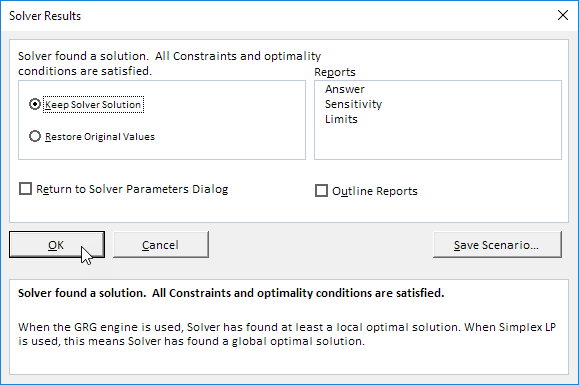
最佳的解决方案:
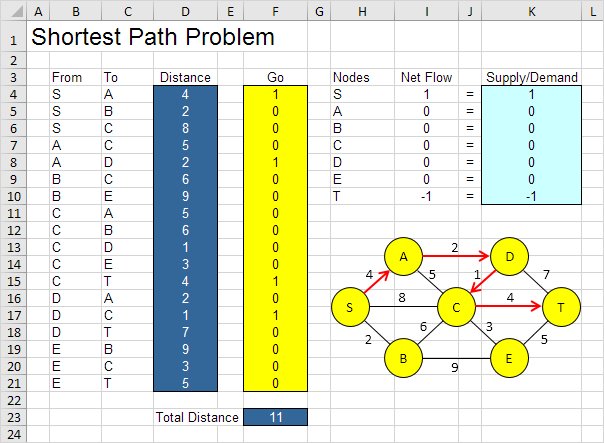
结论:SADCT是具有11的总距离的最短路径