在Excel中标准差
STDEV.P| 链接:#stdev.s [STDEV.S]
本页说明如何计算基于使用Excel中的STDEV.P功能以及如何估计基于使用Excel中的STDEV.S功能的样本标准差的总体的标准偏差。
[[what-is-standard-deviation?]]
=== 什么是标准差?
标准差是一个数字,告诉你数字多远是从他们的意思。
1。例如,数字下方具有为10的平均值(平均)
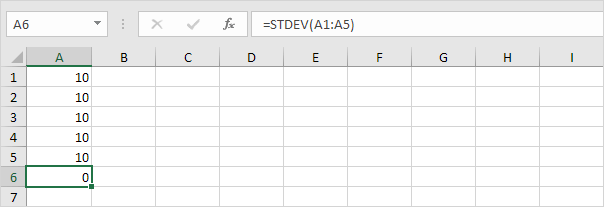
说明:数字是所有这些意味着没有变化相同。其结果是,这些数字都为零的标准偏差。
STDEV函数是一个古老的功能。 Microsoft Excel中建议使用产生完全相同的结果,新STEDV.S功能。
低于2的数字也有10平均值(平均)
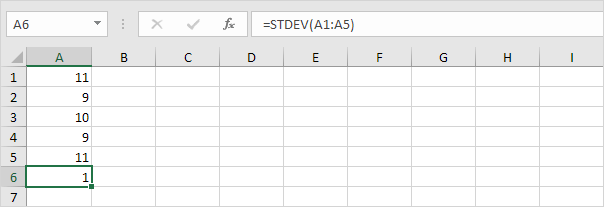
说明:数字是接近均值。其结果是,这些数字具有低标准偏差。
低于3的数字也有10平均值(平均)
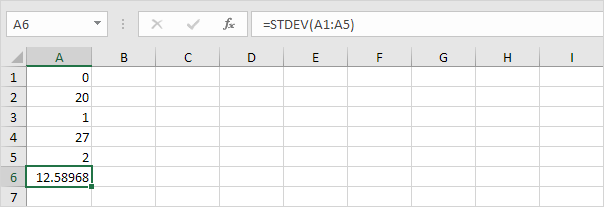
说明:在数字传播出去。其结果是,数字有高标准偏差。
STDEV.P
该STDEV.P功能(P代表人口)在Excel计算基于整个人口的标准偏差。例如,你在教一组5名学生的。你把所有学生的考试成绩。整个群由5个数据点。所述STDEV.P函数使用以下公式:
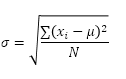
在此实例中,X〜1〜= 5,X〜2〜= 1,X〜3〜= 4,X〜4〜= 6,X〜5〜= 9,μ= 5(平均),N = 5(数据点的数目)。
1.计算的平均值(μ)。
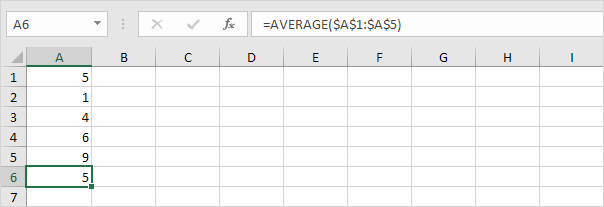
2.对于每个数目,计算出平均值的距离。
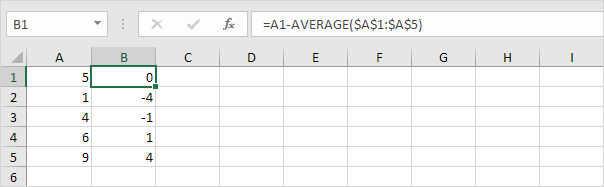
3.对于每个数,平方该距离。
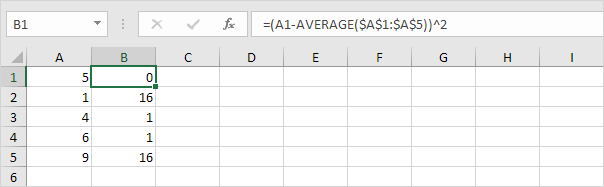
4.总和(Σ)这些值。
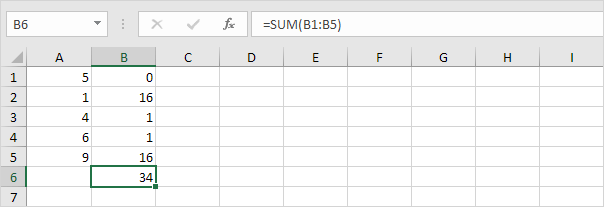
5.除以数据点(N = 5)的数目。
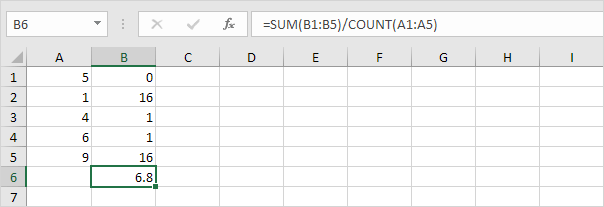
平方根。
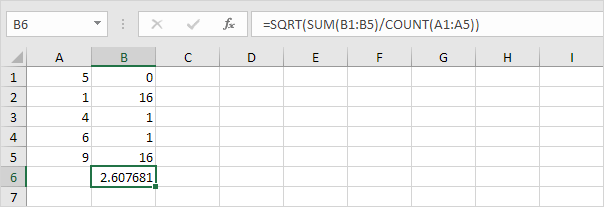
7.幸运的是,在Excel中STDEV.P功能可以执行所有这些步骤你。
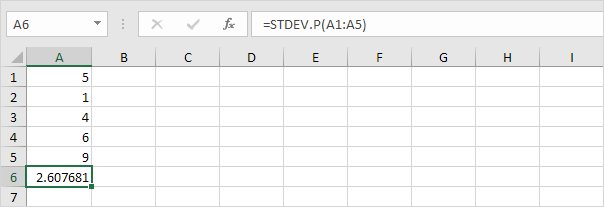
STDEV.S
该STDEV.S功能(S代表样本)在Excel估算基于样本的标准偏差。例如,你在教一大群学生。你只有5名学生的考试成绩。
样本数量等于5。STDEV.S函数使用以下公式:
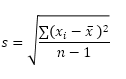
在此实例中,X〜1〜= 5,X〜2〜= 1,X〜3〜= 4,X〜4〜= 6,X〜5〜= 9(相同的数字如上),X = 5(样品意味着)中,n = 5(样本大小)。
以上但在步骤5除n-1而不是N. 1重复步骤1-5
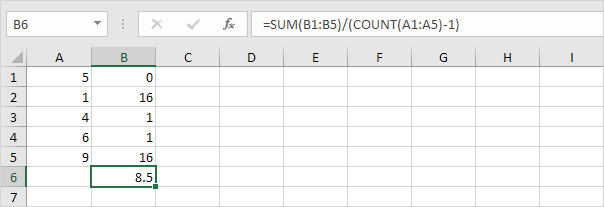
平方根。
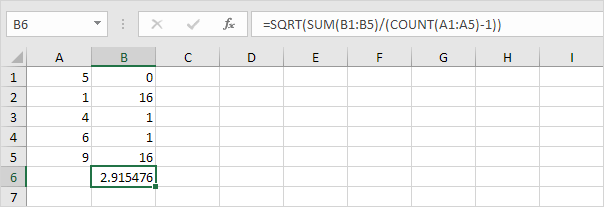
3.幸运的是,在Excel中STDEV.S功能可以执行所有这些步骤你。
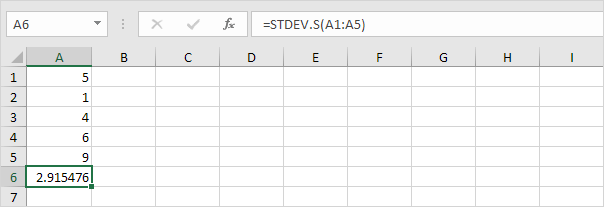
注意:为什么我们用n分 – 1,而不是由n个,当我们估算基于样本的标准偏差?贝塞尔修正状态,由N-1,而不是除以n给出了标准偏差的更好的估计。