Maximale Durchfluss Problem in Excel
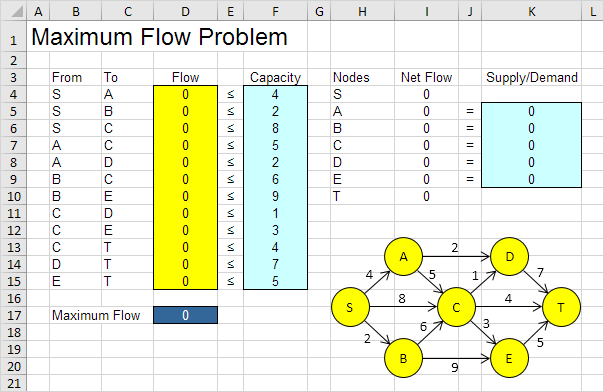
Verwenden Sie den Löser in Excel den maximalen Durchfluss von dem Knoten S zu dem Knoten in einem gerichteten T-Netzwerk zu finden. Punkte in einem Netzwerk werden als Knoten bezeichnet (S, A, B, C, D, E und T). Linien in einem Netzwerk genannt Bögen (SA, SB, SC, AC usw.).
Formulieren Sie das Modell
Das Modell werden wir Blicke zu lösen, wie in Excel folgt.
-
Um dieses maximale Strömungsproblem, beantworten Sie die folgenden drei Fragen zu formulieren.
\ein. Was sind die Entscheidungen getroffen werden? Für dieses Problem müssen wir Excel den Fluss auf jedem Bogen zu finden. wenn die Strömung auf SB zum Beispiel 2 ist, Zelle D5 gleich 2
\ B. Was sind die Einschränkungen für diese Entscheidungen? Der Nettofluß (Flow Out – Durchfluss In) von Knoten A, B, C, D und E sollten auf 0. Mit anderen Worten, Flow Out = Strömungs In gleich sein. Auch hat jeder Bogen eine feste Kapazität. Die Strömung auf jedem Bogen soll als diese Kapazität geringer sein.
\ C. Wie hoch ist der Gesamtleistungsmaßstab für diese Entscheidungen? Das Gesamtmaß der Leistung ist die maximale Strömung, so dass das Ziel ist, diese Menge zu maximieren. Der maximale Durchfluss ist gleich der Strömung aus Knoten S.
-
Um das Modell leichter zu verstehen, die folgenden Bereiche nennen.
|
Range Name |
Cells |
|
From |
B4:B15 |
|
To |
C4:C15 |
|
Flow |
D4:D15 |
|
Capacity |
F4:F15 |
|
SupplyDemand |
K5:K9 |
|
MaximumFlow |
D17 |
-
Legen Sie die folgenden Funktionen.
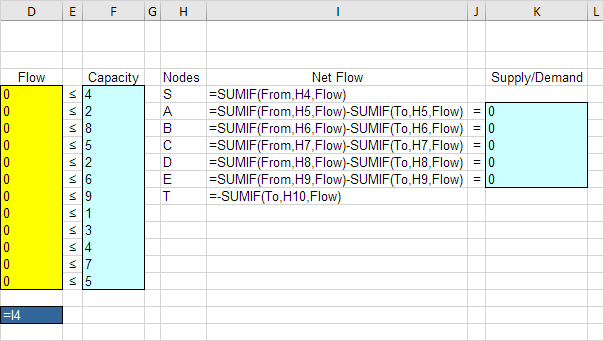
Erläuterung: Der SUMIF Funktionen berechnen den Nettofluss von jedem Knoten. Für Knoten A, fasst die erste SUMIF Funktion die Werte in der Flow-Säule mit einem „A“ in der Spalte Von (Flow Out). Die zweite Funktion SUMIF summiert die Werte in der Flow-Säule mit einem „A“ in der Spalte um (Flow In). Maximaler Durchfluss gleich den Wert in Zelle I4, das den den Knotens S. ausfließen wird, weil der Knoten A, B, C, D und E einen Nettofluß von 0, fließt aus Knoten S haben gleiche Strömungs In dem Knoten T.
Trial and Error
Mit dieser Formulierung wird es einfach, jede Probelösung zu analysieren.
-
Zum Beispiel kann der SADT-Pfad mit einem Fluss von 2. Der Weg SCT mit einem Fluss von 4. Der Pfad SBET mit einem Fluss von 2. Diese Pfade givea Gesamtfluß von 8.
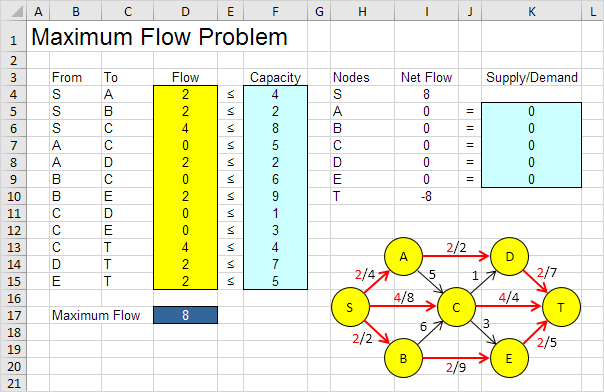
Es ist nicht zu verwenden Versuch und Irrtum notwendig. Wir werden als nächstes beschreiben, wie die Excel Solver schnell verwendet werden können, um die optimale Lösung zu finden.
Lösen Sie das Modell
Um die optimale Lösung zu finden, führen Sie die folgenden Schritte.
-
Wählen Sie auf der Registerkarte Daten in der Gruppe Analyse auf Solver.
Hinweis: kann nicht die Solver-Taste finden? Klicken Sie hier, um das Add-In Solver zu laden.
Geben Sie den Solver-Parameter (weiter lesen). Das Ergebnis sollte mit dem Bild übereinstimmen.
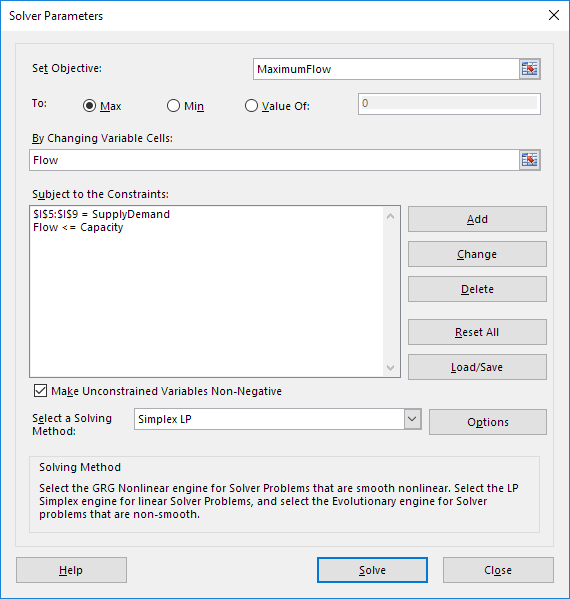
Sie haben die Wahl der Bereichsnamen eingeben oder in der Tabelle auf die Zellen klicken.
Geben Sie MaximumFlow für die Ziel-2.
-
Klicken Sie auf Max.
-
Geben Sie Fluss für die sich ändernden Variable Zellen.
-
Klicken Sie auf Fügen Sie die folgende Einschränkung einzugeben.
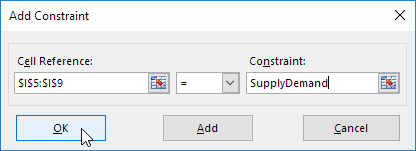
-
Klicken Sie auf Fügen Sie die folgende Einschränkung einzugeben.
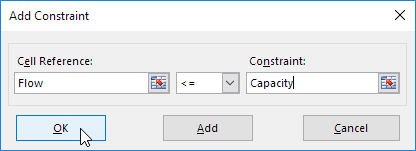
-
Prüfen ‚Make Unconstrained Variablen Non-Negative‘ und wählen Sie ‚Simplex LP‘.
-
Klicken Sie abschließend lösen.
Ergebnis:
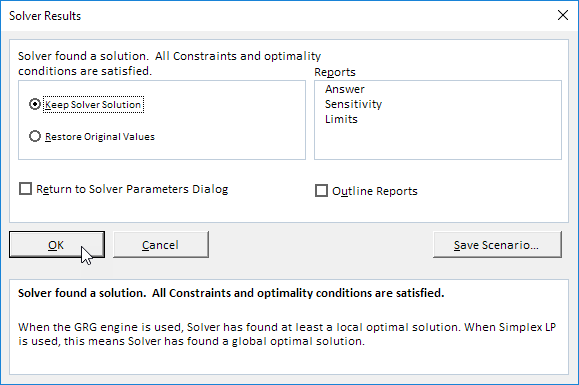
Die optimale Lösung:
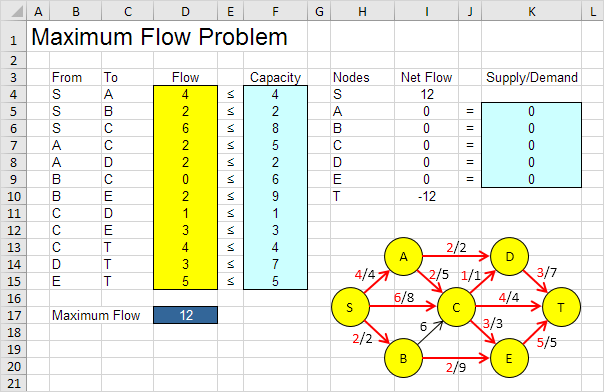
Schlussfolgerung: Der Pfad SADT mit einem Fluss von 2. Die Bahn SCT mit einer Strömung von 4. Der Pfad SBET mit einem Fluss von 2. Der Weg SCET mit einem Fluss von 2. Die Bahn SACET mit einem Fluss von 1. Der Weg SACDT mit einem Fluss von 1 givea Diese Pfade maximalen Strom von 12