Wie die IMDIV Funktion in Excel verwenden
In diesem Artikel erfahren Sie, wie Sie die IMDIV-Funktion in Excel verwenden.
KOMPLEXE Zahl (Zahl) in Excel, abgeleitet für mathematische Zahlen mit reellen und imaginären Koeffizienten. In der Mathematik nennen wir es den Koeffizienten von i oder j (iota).
i = √-1 Quadratwurzel einer negativen Zahl ist nicht möglich, daher wird √-1 zu Berechnungszwecken als imaginär bezeichnet und als iota (i oder j) bezeichnet. Zur Berechnung eines Begriffs wie unten gezeigt.
2 + √-25 = 2 + √-125 = 2 + √-125 = 2 + √-1 5 = 2 + 5i Diese hier Gleichung ist eine komplexe Zahl (inumber) mit 2 verschiedenen Teilen, die als Realteil und Imaginärteil bezeichnet werden Der Koeffizient von iota (i), der 5 ist, wird als Imaginärteil und der andere Teil 2 * als Realteil der komplexen Zahl bezeichnet.
Die komplexe Zahl (inumber) wird im X i * Y-Format geschrieben.
Komplexe Division einer komplexen Zahl (X1 + iY1) & (X2 + i * Y2)
ist gegeben durch (X1 + iY1) / (X2 + i * Y2) = [(X1.X2 + Y1.Y2) + (Y1.X2 X1.Y2) i] / X2.X2 + Y2.Y2 Hier X & Y. sind die Koeffizienten des Real- und Imaginärteils der komplexen Zahl (inumber).
Die IMDIV-Funktion gibt die Division der komplexen Zahl (inumber)
zurück sowohl Real- als auch Imaginärteil haben.
Syntax:
=IMDIV (inumber1 , inumber2)
Nummer 1: Erste komplexe Zahl, die geteilt werden soll.
Nummer 2: Zweite komplexe Zahl, die durch die erste komplexe Zahl geteilt werden soll.
Lassen Sie uns diese Funktion anhand eines Beispiels verstehen.
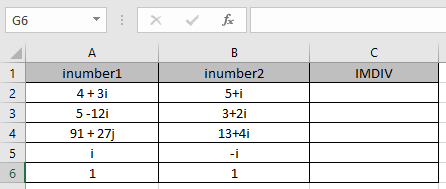
Hier haben wir Werte, bei denen wir die komplexe Aufteilung der eingegebenen komplexen Zahl (Anzahl)
erhalten müssen Verwenden Sie die Formel:
=IMDIV (A2, B2)
A2: Nummer 1 (komplexe Nummer) als Zellreferenz.
A2: Nummer 2 (komplexe Nummer) als Zellreferenz.
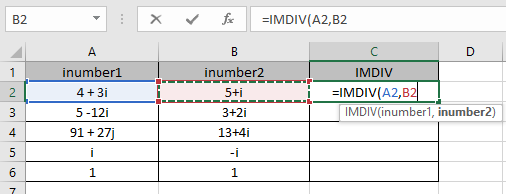
Argumente für die Funktion werden als Zellreferenz angegeben.
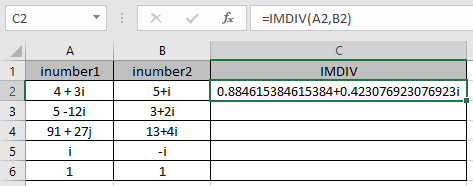
Wie Sie sehen können, führt die komplexe Zahl die Divisionsoperation aus.
Die mathematische Formulierung wird wie unten gezeigt durchgeführt.
5 + i – (4 – i) = (5 – 4) + (i + i) = 1 + 2i Kopieren Sie nun die Formel mit der Tastenkombination Strg + D in die anderen verbleibenden Zellen.
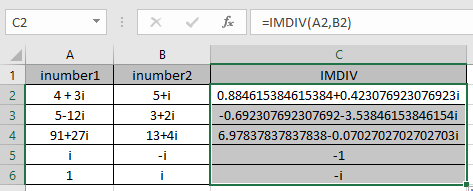
Die hier gezeigte Tabelle erklärt mehr über die Ergebnisse
|
inumber1 |
inumber2 |
Real part 1 (X1) |
Imaginary part (Y1) |
Real part (X1) |
Imaginary part (Y2) |
|
i |
– i |
0 |
1 |
0 |
– 1 |
|
1 |
i |
1 |
0 |
0 |
1 |
Wie Sie sehen können, liefert die IMDIV-Funktionsformel gute Ergebnisse.
Hinweis:
-
Die Formel gibt die #NUM! Fehler, wenn die komplexe Zahl keine Kleinbuchstaben i oder j (iota) enthält.
-
Die Formel gibt den #WERT zurück! Fehler, wenn die komplexe Nummer nicht das richtige Format für komplexe Nummern hat.
Ich hoffe, Sie haben verstanden, wie die IMDIV-Funktion und die verweisende Zelle in Excel verwendet werden. Weitere Artikel zu mathematischen Funktionen von Excel finden Sie hier.
Bitte zögern Sie nicht, Ihre Anfrage oder Ihr Feedback zu dem oben genannten Artikel zu äußern.
Verwandte Artikel
link: / math-functions-excel-log10-function [Verwendung der Excel LOG10-Funktion]
link: / excel-formel-und-funktion-wie-man-die-imexp-funktion-in-excel benutzt [wie man die IMEXP-Funktion in Excel benutzt]
link: / excel-formel-und-funktion-wie-man-die-imkonjugierte-funktion-in-excel benutzt [wie man die IMCONJUGATE-Funktion in Excel benutzt]
link: / mathematische-funktionen-wie-man-die-imargument-funktion-in-excel benutzt [wie man die IMARGUMENT-Funktion in Excel benutzt]
Beliebte Artikel
link: / excel-generals-wie-man-eine-dropdown-liste-in-microsoft-excel bearbeitet [Dropdown-Liste bearbeiten]
link: / tips-bedingte-formatierung-mit-if-Anweisung [Wenn mit bedingter Formatierung]
link: / logische Formeln-wenn-Funktion-mit-Platzhaltern [Wenn mit Platzhaltern]
link: / lookup-formulas-vlookup-by-date-in-excel [Vlookup-by-date]