In diesem Artikel erfahren Sie, wie Sie den gewichteten Durchschnitt in Microsoft Excel berechnen.

Das Konzept des Durchschnitts stammt aus der Mathematik. Der Durchschnitt kann als das Ergebnis definiert werden, das wir erhalten, nachdem wir mehrere Mengen addiert und diese Summe dann durch die Anzahl der Mengen dividiert haben.

Der gewichtete Mittelwert ähnelt dem arithmetischen Mittelwert, bei dem anstelle jedes Datenpunkts, der gleichermaßen zum endgültigen Durchschnitt beiträgt, einige Datenpunkte mehr als andere beitragen.

Wenn alle Gewichte gleich sind, bleibt der gewichtete Mittelwert der gleiche wie der arithmetische Mittelwert.

Lassen Sie uns anhand eines Beispiels mehr verstehen:

Wir möchten den Durchschnitt der Noten eines Schülers in vier Fächern berechnen. * In Spalte A haben wir Fach und in Spalte B haben wir Noten

img1

Wir addieren die Zahlen und dividieren das Ergebnis durch die Anzahl der Probanden (75 + 90 + 65 + 85) / 4 = 78,5 * Dies ist der ungewichtete Durchschnitt, da wir in diesem Szenario jeder Zahl dieselbe Priorität zugewiesen haben.

Der gewichtete Durchschnitt ist eine Art von Durchschnitt, bei dem beim Ermitteln des Durchschnitts auch das Gewicht berücksichtigt wird, da dieses eine Element möglicherweise wesentlich zum Endergebnis beiträgt als ein anderes Element.

Nun wollen wir mit einem anderen Beispiel verstehen

In Spalte A haben wir Betreff & in Spalte B haben wir Markierungen

img2

Nehmen wir an, dass ein Student aufgrund seines Interesses an Mathematik eine Zulassung zum Math College erhalten möchte. Das College-Team hat erkannt, dass ein höherer Prozentsatz der Studenten aufgrund der guten verfügbaren Fakultäten und ihrer hervorragenden Erfolgsbilanz für das Math eine Zulassung zum College erhalten möchte Das College wird also offensichtlich mehr Wert auf die Mathematiknoten legen, und daher haben sie die Idee, jedem Fach wie folgt Gewicht zuzuweisen:

img3

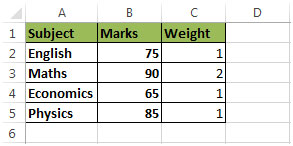
Dies zeigt, dass das College die Noten von Mathematik im Vergleich zu Noten anderer Fächer stärker betont. Wenn wir Noten mit Gewicht multiplizieren, dh (Noten x Gewicht), erhalten wir: 75 x 1) + (90 x 2) + (65 x) 1) + (85 x 1 / (1 + 2 + 1 + 1)

  • Dies wird 81

img4

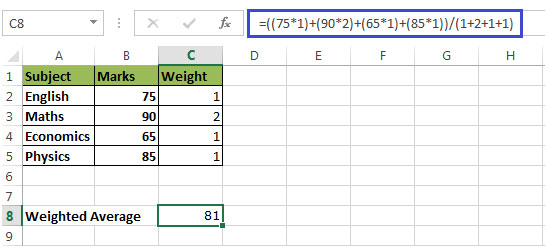
sein * Der gewichtete Durchschnitt (81) ist höher als der ungewichtete Durchschnitt (78,5)

  • In diesem Fall haben die Noten der Mathematik mehr zur endgültigen Ausgabe beigetragen als jedes andere Element.

  • Mit dem oben gezeigten Beispiel haben wir den Unterschied zwischen gewichtetem und ungewichtetem Durchschnitt verstanden.