A continuación vamos a ver un programa en Excel VBA que resuelve un pequeño ejemplo de un problema de la mochila.

Definición: dado un conjunto de elementos, cada uno con un peso y un valor, determinar los elementos a incluir en una colección de modo que el valor total es tan grande como sea posible y el peso total es menor que un límite dado.

Su nombre se deriva del problema enfrentado por alguien que está limitado por una mochila de tamaño fijo y debe llenarlo con los artículos más útiles.

Ejemplo: 5 elementos con pesos, valores y límite como dadas.

Knapsack Problem Image

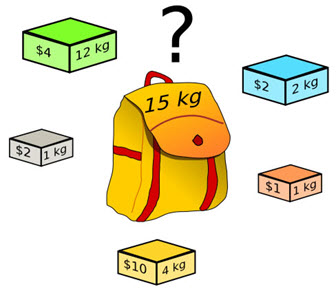
En Excel este problema se ve de la siguiente manera:

Knapsack Problem Example

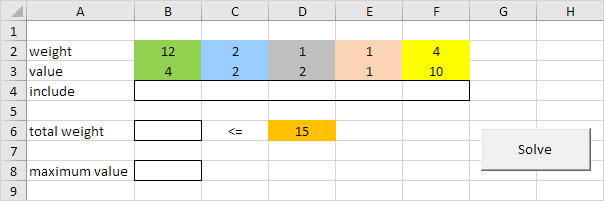
  1. En primer lugar, declaramos cinco variables de tipo doble con nombres límite, peso, valor, pesoTotal y MaximumValue.

Dim limit As Double, weight As Double, value As Double, totalWeight As Double, maximumValue As Double

  1. A continuación, declaramos cinco variables de tipo entero con con los nombres i, j, k, l, m.

Dim i, j, k, l, m As Integer

  1. inicializar dos variables. Inicializar el límite variable con el valor de la celda D6. Inicializamos la variable MaximumValue con valor 0.

limit = Range("D6").value

maximumValue = 0

  1. A continuación, se comprueba cada posible solución. Podemos incluir ya sea un elemento (1) o dejarlo fuera (0). Empezamos 5 Para bucles siguiente. Uno para cada elemento.

For i = 0 To 1

For j = 0 To 1

For k = 0 To 1

For l = 0 To 1

For m = 0 To 1

  1. Se calcula el peso y el valor de una posible solución.

weight = 12  i + 2  j + 1  k + 1  l + 4  m

value = 4  i + 2  j + 2  k + 1  l + 10  m

  1. Sólo si el valor es mayor que MaximumValue y el peso es menor que el límite, hemos encontrado una nueva solución mejor.

If value > maximumValue And weight <= limit Then

  1. Si esto es cierto, se escribe la nueva solución a la fila 4, el peso de pesoTotal y valor a MaximumValue.

Range("B4").value = i

Range("C4").value = j

Range("D4").value = k

Range("E4").value = l

Range("F4").value = m

totalWeight = weight

maximumValue = value

  1. No se olvide de cerrar la instrucción if.

End If

  1. No se olvide de cerrar la 5 Para bucles siguiente.

Next m

Next l

Next k

Next j

Next i

Excel VBA comprueba cada solución posible de esta manera y como resultado aparecerá la solución óptima en la fila 4. Recuerde que 1 significa que incluimos un artículo, 0 significa que dejarlo fuera.

  1. Por último, escribir pesoTotal y MaximumValue de la solución óptima para respectivamente la celda B6 y B8.

Range("B6").value = totalWeight

Range("B8").value = maximumValue

Prueba 11. el programa.

Resultado:

Knapsack Problem Result

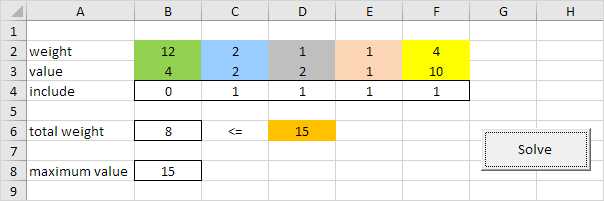
Conclusión: es óptima para incluir los últimos cuatro elementos con un valor máximo de 15. Esta solución con un peso total de 2 + 1 + 1 + 4 = 8 no exceda el límite de 15.

Nota: al hacer la variable de pesos y valores que puede resolver cualquier problema de la mochila de este tamaño (véase el archivo de Excel descargable).