Excelで最短経路問題

モデルは、我々は、Excelで次のようにルックスを解決しようとしています。

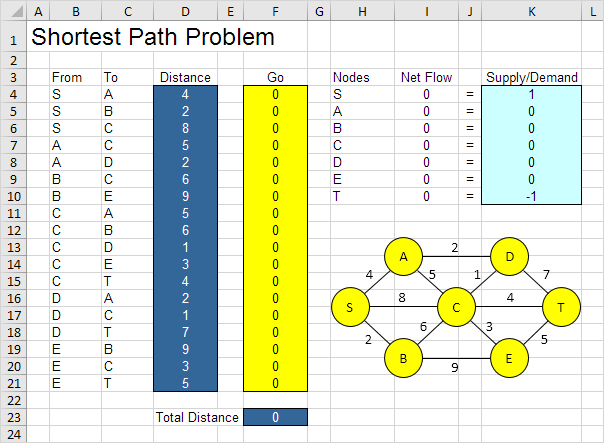
この最短経路問題を定式化するために1.、以下の3つの質問に答えます。

\。なされるべき決定事項は何ですか？この問題のために、私たちは、アークが最短パスかどうか（はい= 1、なし= 0）上にあるかどうかを確認するために、Excelが必要です。 SBは、最短パスの一部である場合、例えば、セルF5は、セルF5は0に等しく、1ない場合等しい

\ B。これらの決定上の制約は何ですか？正味の流れ（フローアウト – フロー内の）各ノードのは、需要/供給に等しいはずです。ノードSは1つの出力アーク（正味の流れ= 1）を持つべきです。ノードTは一つだけ入ってくるアーク（ネットフロー= -1）が必要です。ノードは最短経路（正味の流れ= 0）、または全く流れ（正味の流れ= 0）にある場合、他のすべてのノードが1つの出力アークと一つ入ってくるアークを有していなければなりません。

\ C。これらの決定のためのパフォーマンスの全体的な尺度は何ですか？目的は、この量を最小化することであるので、性能の全体的な尺度は、最短経路の合計距離です。

以下の範囲に名前を付ける、理解するためにモデルを容易にするために2。

次の関数を挿入3.。

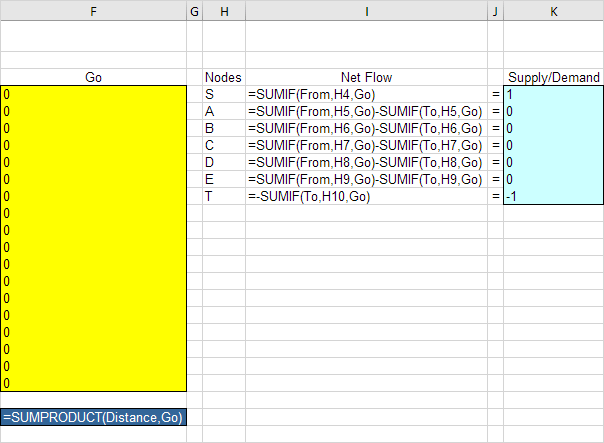
説明： SUMIF関数は、各ノードの正味の流れを計算します。ノードSは、SUMIF関数は、カラムから「S」に行く列の値を合計します。結果として、唯一のF4、F5、細胞またはF6は1（1つの出力アーク）とすることができます。ノードTのために、SUMIF関数は、に列の「T」で行く列の値を合計します。結果として、唯一のセルF15、F18またはF21は1（1つの入ってくるアーク）とすることができます。他のすべてのノードの場合は、Excelは、Fromと列に見えます。総距離は、距離や移動のSUMPRODUCTに等しいです。

この処方では、それがどの試行解を分析することが容易になります。

1.たとえば、パスSBETは16の総距離を有する

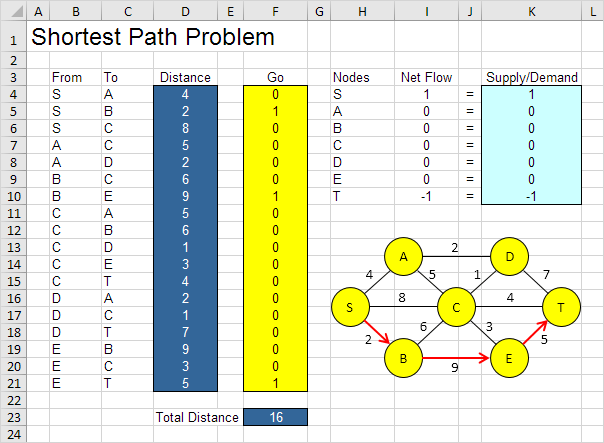
試行錯誤を使用する必要はありません。私たちは、Excelソルバーはすぐに最適なソリューションを見つけるために使用することができる方法を次の記述しなければなりません。

最適解を見つけるには、次の手順を実行します。

注：ソルバーのボタンを見つけることができませんか？ソルバーアドインをロードするにはここをクリックしてください。

ソルバーパラメータを（読み）を入力します。結果は以下の画像と一致している必要があります。

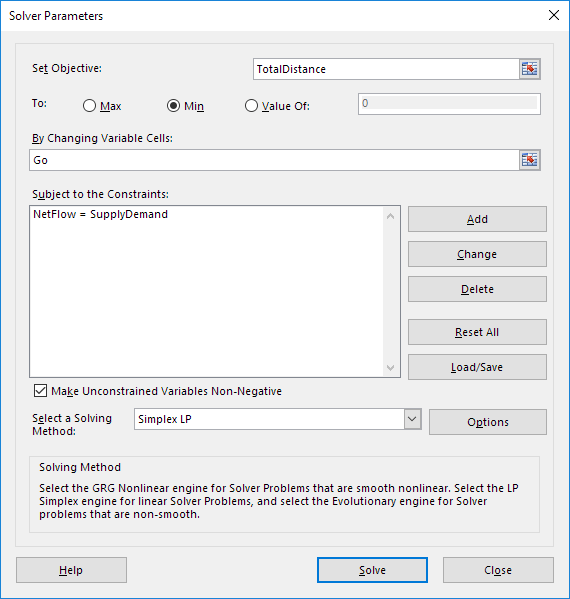
あなたは、範囲名を入力するか、スプレッドシート内のセルをクリックするかを選択できます。

目的のためにTotalDistanceを入力します。

分]をクリックします。

変更する変数のセルのために行くを入力します。

5.次の制約を入力して[追加]をクリックします。

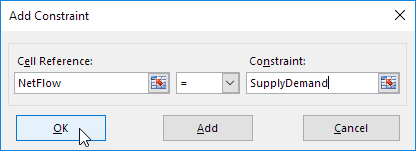
6.チェック「制約のない変数非負を作る」と「シンプレックスLP」を選択します。

7.最後に、解決をクリックします。

結果：

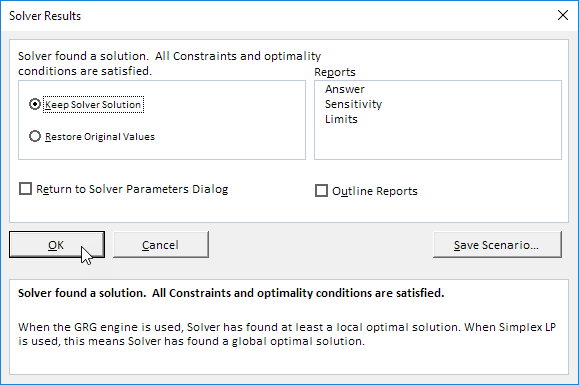
最適なソリューション：

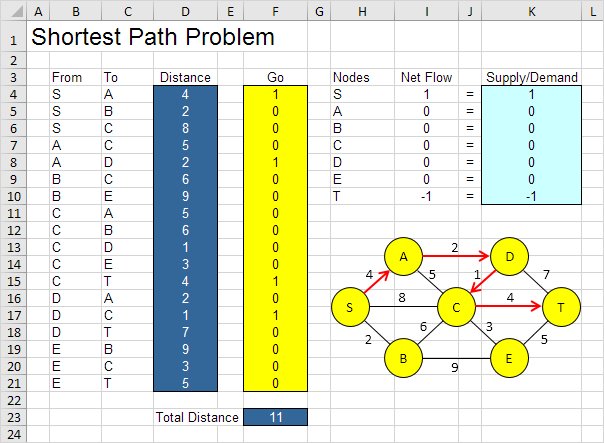
結論：SADCTは11の総距離と最短経路である