Box et Plot dans Excel Moustaches
Cet exemple vous apprend comment créer une boîte et dans Excel moustaches. Une boîte et moustaches montre la valeur minimale, d’abord lien: / exemples percentiles-quartiles [quartile], la médiane, le troisième quartile et la valeur maximale d’un ensemble de données.
Simple boîte et moustaches
-
Par exemple, sélectionnez la plage A1: A7.
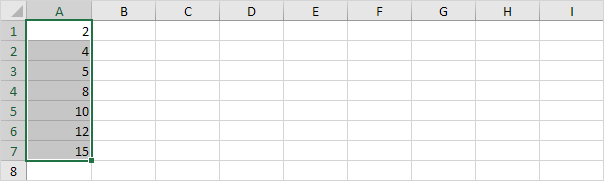
Remarque: vous ne devez pas trier les points de données du plus petit au plus grand, mais il vous aidera à comprendre la boîte et moustaches.
-
Dans l’onglet Insertion, dans le groupe Graphiques, cliquez sur le symbole statistique graphique.

-
Cliquez sur Boîte et Moustaches.
Résultat:
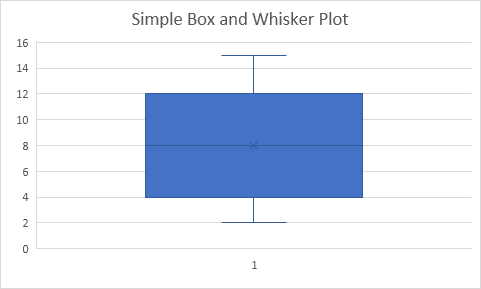
Explication: la ligne médiane de la boîte représente la médiane ou le numéro du milieu (8). Le x dans la boîte représente la moyenne (8 également dans cet exemple). La médiane divise l’ensemble de données en une moitié inférieure \ {2, 4, 5} et une moitié supérieure \ {10, 12, 15}. La ligne de fond de la boîte représente la médiane de la moitié inférieure ou 1er quartile (4). La ligne de sommet de la boîte représente la médiane de la moitié supérieure ou 3ème quartile (12). Les moustaches (lignes verticales) étendent à partir des extrémités de la boîte à la valeur minimale (2) et la valeur maximale (15).
Outliers
-
Par exemple, sélectionnez la plage A1: A11.
Note: le nombre médian ou intermédiaire (8) divise l’ensemble de données en deux moitiés: \ {1, 2, 2, 4, 5} et \ {10, 12, 15, 18, 35}. Le premier quartile (Q ~ 1 ~) est la médiane de la première moitié. Q ~ 1 ~ = 2. Le troisième quartile (Q ~ 3 ~) est la médiane de la seconde moitié. Q ~ 3 ~ = 15.
-
Dans l’onglet Insertion, dans le groupe Graphiques, cliquez sur le symbole statistique graphique.

-
Cliquez sur Boîte et Moustaches.

Résultat:
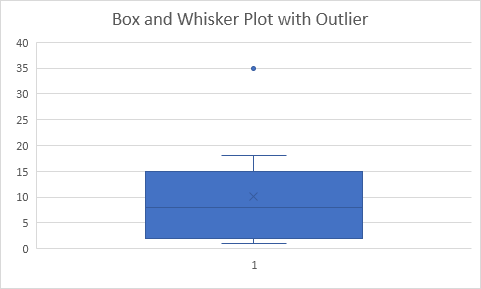
Explication: la gamme interquartile (IQR) est définie comme étant la distance entre le premier quartile et le troisième quartile. Dans cet exemple, IQR = Q ~ 3 ~ – Q ~ 1 ~ = 15 – 2 = 13 points de données A est considéré comme une valeur aberrante si elle dépasse d’une distance de 1,5 fois le IQR en dessous du premier quartile (Q ~ 1 ~ – 1,5 IQR = 2 à 1,5 13 = -17,5) ou 1,5 fois le IQR au-dessus du troisième quartile (Q ~ 3 ~ + 1,5 IQR = 15 + 1,5 13 = 34,5). Par conséquent, dans cet exemple, 35 est considéré comme une valeur aberrante. En conséquence, la partie supérieure se prolonge whisker à la plus grande valeur (18) à l’intérieur de cette plage.
-
Modifiez les dernières données indiquent 34.
Résultat:
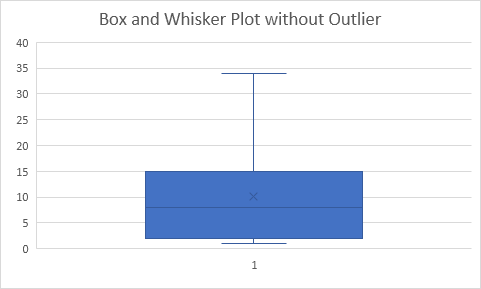
Explication: tous les points de données sont entre -17,5 et 34,5. En conséquence, les moustaches étendent à la valeur minimale (2) et la valeur maximale (34).
Box Calculs Plot
La plupart du temps, vous ne pouvez pas possible de déterminer facilement le 1er quartile et 3e quartile sans effectuer des calculs.
-
Par exemple, sélectionnez le nombre pair de points de données ci-dessous.
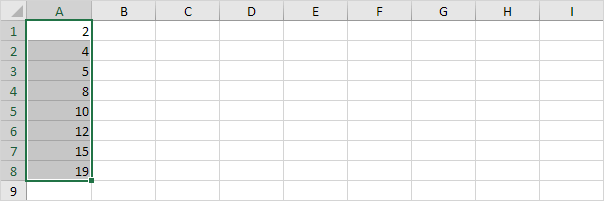
-
Dans l’onglet Insertion, dans le groupe Graphiques, cliquez sur le symbole statistique graphique.

-
Cliquez sur Boîte et Moustaches.

Résultat:
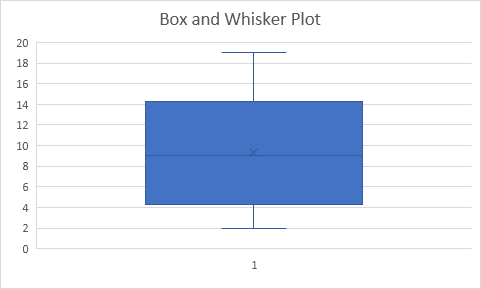
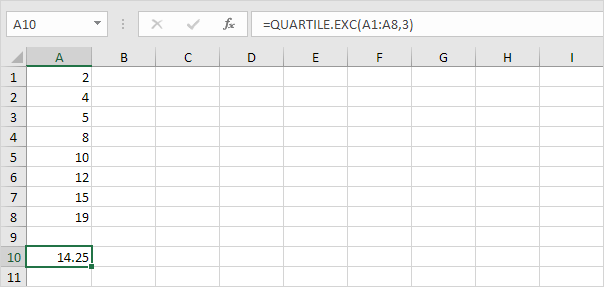
Explication: Excel utilise la fonction QUARTILE.EXC pour calculer le 1er quartile (Q ~ 1 ~), 2e quartile (Q ~ 2 ~ ou médiane) et 3e quartile (Q ~ 3 ~).
Cette fonction interpole entre deux valeurs pour calculer un quartile.
Dans cet exemple, n = 8 (nombre de points de données).
-
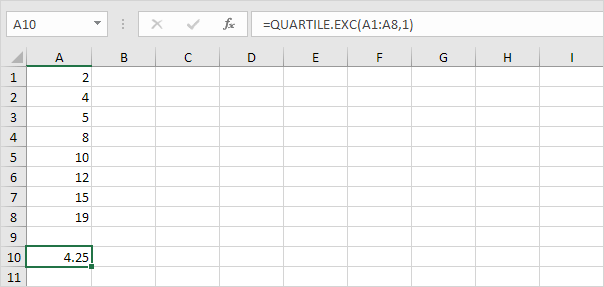
Q ~ 1 ~ = 1/4 (n + 1) ième valeur = 1/4 (8 + 1) ième valeur = 2 1 / quatrième valeur = 4 + 1/4 (4/5) = 4 1/4 . Vous pouvez vérifier ce numéro en utilisant la fonction QUARTILE.EXC ou regardant la boîte et moustaches.
-
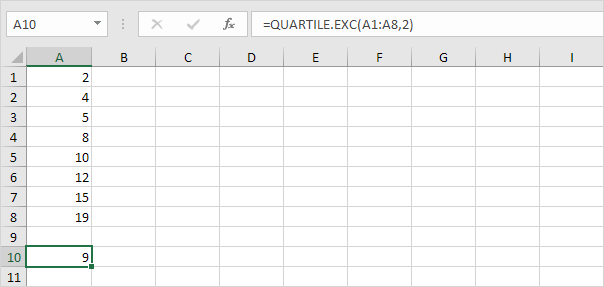
Q ~ 2 ~ = 1/2 (n + 1) ième valeur = 1/2 (8 + 1) ième valeur = 4 1 / valeur 2th = 8 + 1/2 (10-8) = 9. Cela rend sens, la médiane est la moyenne des deux chiffres du milieu.
-
Q ~ 3 ~ = 3/4 (n + 1) ième valeur = 3/4 (8 + 1) ième valeur = 6 3/4 value = 12 + 3/4 * (15-12) = 14 1 / 4. Encore une fois, vous pouvez vérifier ce numéro en utilisant la fonction QUARTILE.EXC ou regardant la boîte et moustaches.