exemple simple TRI | Valeurs actuelles | règle de TRI

Utilisez la fonction TRI dans Excel pour calculer le taux de rendement interne d’un projet. Le taux de rendement interne est le taux d’actualisation qui rend la valeur actuelle nette égale à zéro.

Exemple simple IRR

Par exemple, le projet A nécessite un investissement initial de 100 $ (B5 cellulaire).

  1. Nous nous attendons à un bénéfice de $ 0 à la fin de la première période, un bénéfice de $ 0 à la fin de la deuxième période et un bénéfice de 152,09 $ à la fin de la troisième période.

Cash Flows

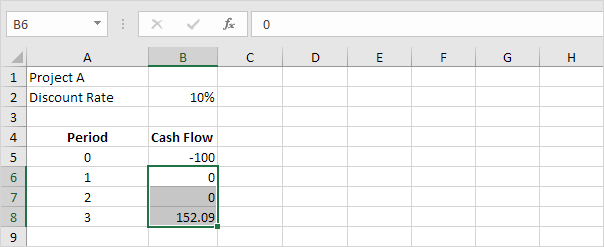
Note: le taux d’actualisation est égal à 10%. Ceci est le taux de rendement des meilleurs investissements alternatifs. Par exemple, vous pouvez aussi mettre votre argent dans un compte d’épargne à un taux d’intérêt de 10%.

  1. Le lien correct : / exemples npv [VAN formule] dans Excel utilise la fonction VAN pour calculer la valeur actuelle d’une série de flux de trésorerie futurs et soustraient l’investissement initial.

Net Present Value

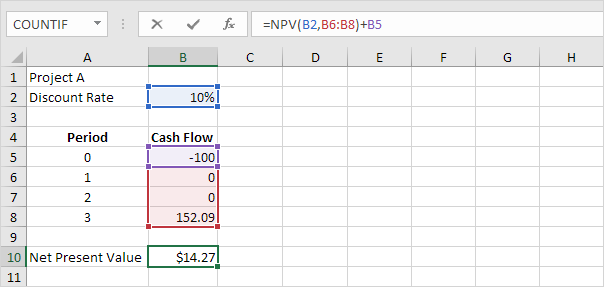
Explication: une valeur actualisée nette positive indique que le taux de rendement du projet dépasse le taux d’actualisation. En d’autres termes, il est préférable d’investir votre argent dans le projet A que de mettre votre argent dans un compte d’épargne à un taux d’intérêt de 10%.

  1. La fonction TRI ci-dessous calcule le taux de rendement interne du projet A.

IRR function in Excel

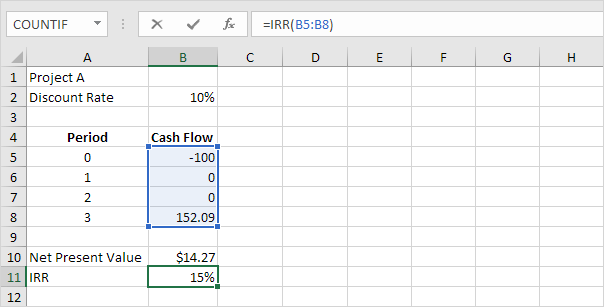
  1. Le taux de rendement interne est le taux d’actualisation qui rend la valeur actuelle nette égale à zéro. Pour voir clairement, remplacer le taux d’actualisation de 10% dans la cellule B2 avec 15%.

Net Present Value of 0

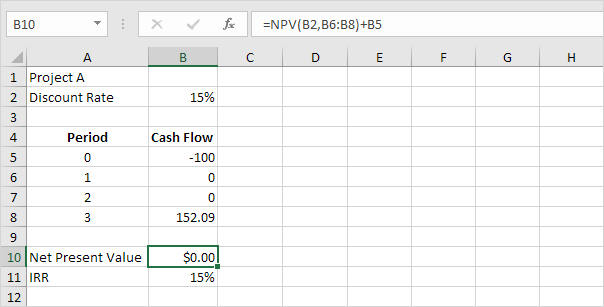
Explication: une valeur actualisée nette de 0 indique que le projet génère un taux de rendement égal au taux d’actualisation. En d’autres termes, les deux options, d’investir votre argent dans le projet A ou de mettre votre argent dans un compte d’épargne à haut rendement représentent un taux d’intérêt de 15%, un rendement égal donnent.

  1. Nous pouvons vérifier cela. Supposons que vous mettez 100 $ dans une banque. Combien votre investissement vaudra après 3 ans à un taux d’intérêt annuel de 15%? La réponse est 152,09 $.

Compound Interest

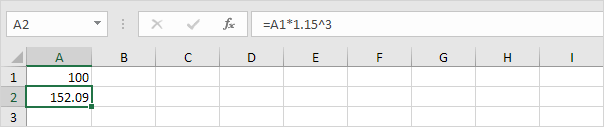
Conclusion: vous pouvez comparer les performances d’un projet à un compte d’épargne avec un taux d’intérêt égal au TRI.

Valeurs actuelles

Par exemple, le projet B nécessite un investissement initial de 100 $ (B5 cellulaire).

Nous nous attendons à un bénéfice de 25 $ à la fin de la première période, un bénéfice de 50 $ à la fin de la deuxième période et un bénéfice de 152,09 $ à la fin de la troisième période.

  1. La fonction IRR ci-dessous calcule le taux de rendement interne du projet B.

Internal Rate of Return

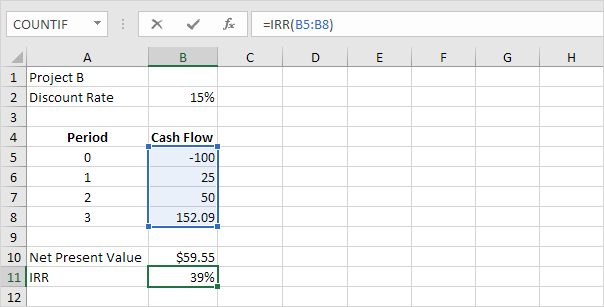
  1. Encore une fois, le taux de rendement interne est le taux d’actualisation qui rend la valeur actuelle nette égale à zéro. Pour voir clairement, remplacer le taux d’actualisation de 15% dans la cellule B2 avec 39%.

NPV equals 0

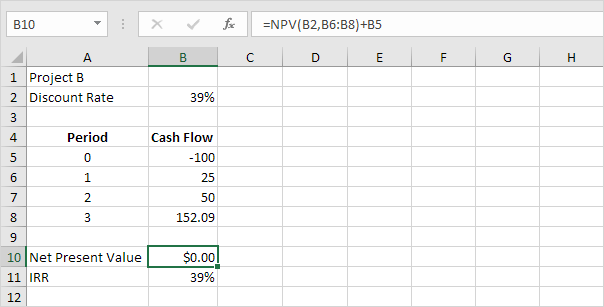
Explication: une valeur actualisée nette de 0 indique que le projet génère un taux de rendement égal au taux d’actualisation. En d’autres termes, les deux options, d’investir votre argent dans le projet B ou de mettre votre argent dans un compte d’épargne à haut rendement représentent un taux d’intérêt de 39%, un rendement égal donnent.

  1. Nous pouvons vérifier cela. Tout d’abord, on calcule la valeur actuelle (pv) de chaque flux de trésorerie. Ensuite, nous somme de ces valeurs.

Sum Present Values

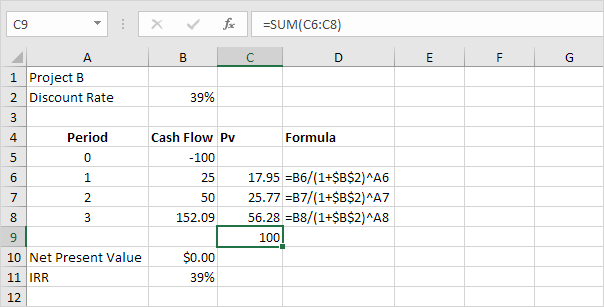
Explication: au lieu d’investir 100 $ dans le projet B, vous pouvez aussi mettre 17,95 $ dans un compte d’épargne pour 1 an, 25,77 $ dans un compte d’épargne pour 2 ans et 56,28 $ dans un compte d’épargne pendant trois ans, à un taux d’intérêt annuel égal au TRI (39%).

règle de TRI

La règle de TRI indique que si le TRI est supérieur au taux de rendement requis, vous devez accepter le projet. Les valeurs de TRI sont fréquemment utilisés pour comparer les investissements.

  1. La fonction TRI ci-dessous calcule le taux de rendement interne du projet X.

IRR

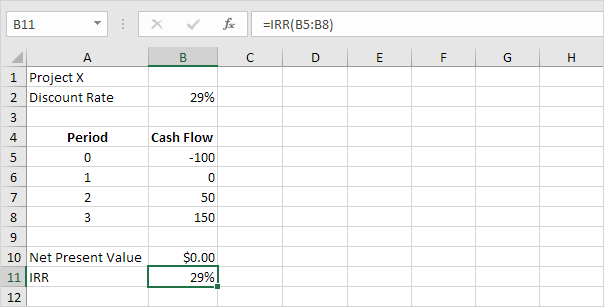
Conclusion: si le taux de rendement requis est égal à 15%, vous devez accepter ce projet parce que le TRI de ce projet est égal à 29%.

  1. La fonction TRI ci-dessous calcule le taux de rendement interne du projet Y.

Higher IRR

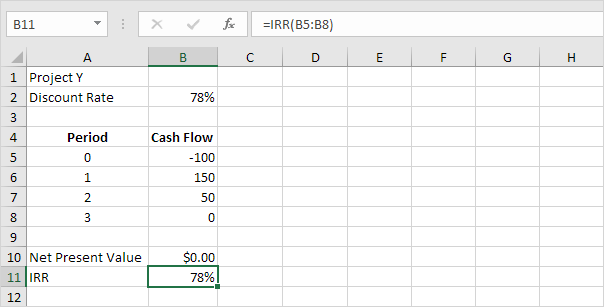
Conclusion: en général, un TRI supérieur indique un meilleur investissement.

Par conséquent, le projet Y est un meilleur investissement que le projet X.

  1. La fonction TRI ci-dessous calcule le taux de rendement interne du projet Z.

Low Cash Flows

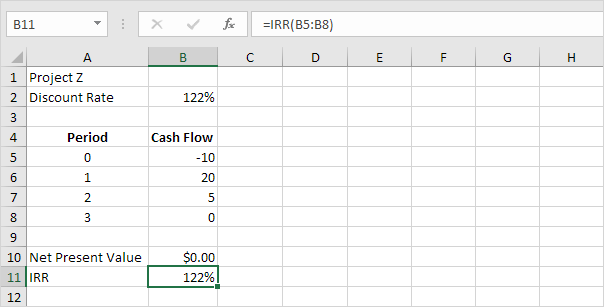
Conclusion: un TRI supérieur n’est pas toujours mieux. Projet Z a un TRI supérieur à Y projet, mais les flux de trésorerie sont beaucoup plus faibles.