R carré | Signification F et P-Valeurs | #coefficients Coefficients | lien: #residuals [] Résiduels

Cet exemple vous enseigne comment exécuter une analyse de régression linéaire dans Excel et comment interpréter le résumé de sortie.

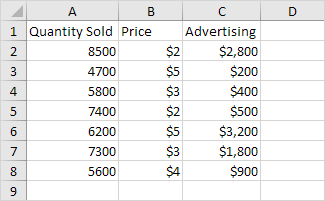
Ci-dessous vous trouverez nos données. La grande question est: est-il une relation entre la quantité vendue (sortie) et prix et publicité (entrée). En d’autres termes: peut-on prédire Quantité Vendu si nous savons Prix et publicité?

Regression Data in Excel

  1. Dans l’onglet Données, dans le groupe d’analyse, cliquez sur l’analyse des données.

Click Data Analysis

Note: ne peut pas trouver le bouton d’analyse des données? Cliquez ici pour charger le complément utilitaire d’analyse.

  1. Sélectionnez la régression et cliquez sur OK.

Select Regression

  1. Sélectionnez la gamme Y (A1: A8). Ceci est la variable prédictive (également appelée variable dépendante).

  2. Sélectionnez la gamme X (B1: C8). Ce sont les variables explicatives (aussi appelées variables indépendantes). Ces colonnes doivent être adjacentes les unes aux autres.

  3. Vérifier les étiquettes.

  4. Cliquez dans la zone Plage de sortie et sélectionnez la cellule A11.

  5. Vérifiez Residuals.

  6. Cliquez sur OK.

Regression Input and Output

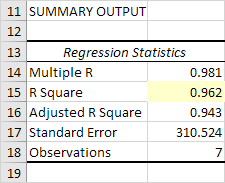
Excel produit la sortie sommaire suivant (arrondi à 3 décimales).

R Carré

R place est égal à 0,962, ce qui est un très bon ajustement. 96% de la variation de la quantité vendue est expliquée par les variables indépendantes Prix et publicité. Le plus proche de 1, plus la ligne de régression (lire) correspond aux données.

R Square

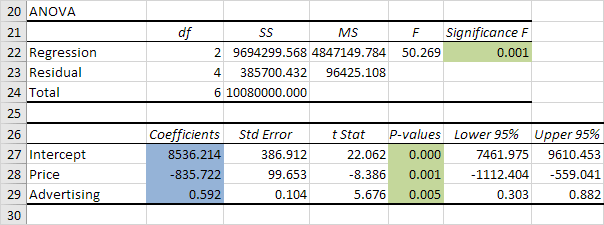
Signification F et les valeurs p

Pour vérifier si vos résultats sont fiables (statistiquement significatif), regardez Signification F (0,001). Si cette valeur est inférieure à 0,05, vous êtes OK.

Si Signification F est supérieure à 0,05, il est probablement préférable de cesser d’utiliser cet ensemble de variables indépendantes. Supprimer une variable avec une forte valeur P (supérieur à 0,05) et exécuter à nouveau jusqu’à ce que la régression Signification F tombe en dessous de 0,05.

La plupart ou toutes les P-valeurs doivent être inférieures en dessous de 0,05. Dans notre exemple, est le cas. (0,000, 0,001 et 0,005).

Anova

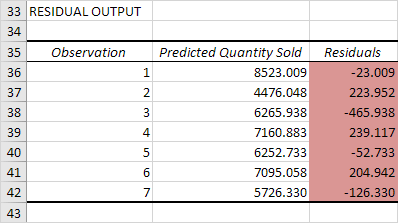
Coefficients

La ligne de régression est: y = Quantité vendue = 8536,214 -835,722 Prix + 0,592 publicité. En d’autres termes, pour chaque unité d’augmentation de prix, la quantité vendue diminue avec 835.722 unités. Pour chaque unité d’augmentation de la publicité, Quantité vendue augmente avec 0,592 unités. Cette information est précieuse.

Vous pouvez également utiliser ces coefficients pour faire une prévision. Par exemple, si le prix est égal à 4 $ et 3000 $ Publicité est égal, vous pourriez être en mesure d’obtenir une quantité vendue de 8536,214 -835,722 4 + 0,592 3000 = 6970.

Résiduels

Les résidus vous montrent la distance les points de données réels sont les fom points de données prévus (en utilisant l’équation). Par exemple, le premier point de données est égale à 8500. En utilisant l’équation, le point de données prédit est égale à 8536,214 -835,722 2 + 0,592 2800 = 8523,009, donnant un résidu de 8500 à 8523,009 = -23,009.

Residuals

Vous pouvez également créer un diagramme de dispersion de ces résidus.

Scatter Plot