? Qu’est-ce que l’écart type | STDEV.P | STDEV.S

Cette page explique comment calculer l’écart-type en fonction de la totalité de la population en utilisant la fonction STDEV.P dans Excel et comment estimer l’écart-type basé sur un échantillon en utilisant la fonction STDEV.S dans Excel.

[[what-is-standard-deviation?]]
=== Quel est l’écart type?

L’écart type est un numéro qui vous indique le nombre sont loin de leur moyenne.

  1. Par exemple, les chiffres ci-dessous ont une moyenne (moyenne) de 10

Standard Deviation of Zero in Excel

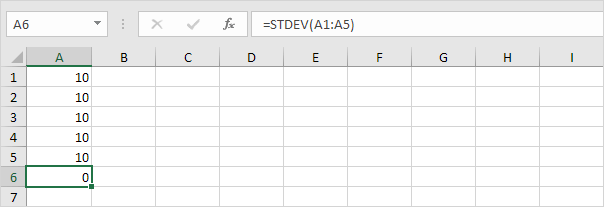
Explication: les chiffres sont tous les mêmes qui signifie qu’il n’y a pas de variation. En conséquence, les chiffres ont un écart-type de zéro.

La fonction ECARTYPE est une ancienne fonction. Microsoft Excel recommande d’utiliser la nouvelle fonction STEDV.S qui produit exactement le même résultat.

  1. Les chiffres ci-dessous ont aussi une moyenne (moyenne) de 10

Low Standard Deviation in Excel

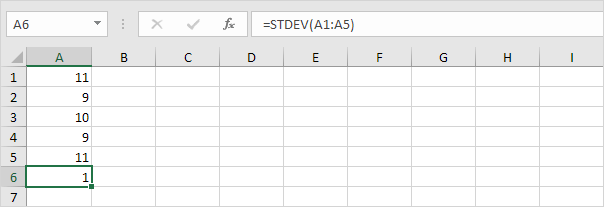
Explication: les chiffres sont proches de la moyenne. En conséquence, les chiffres ont un faible écart type.

  1. Les chiffres ci-dessous ont aussi une moyenne (moyenne) de 10

High Standard Deviation in Excel

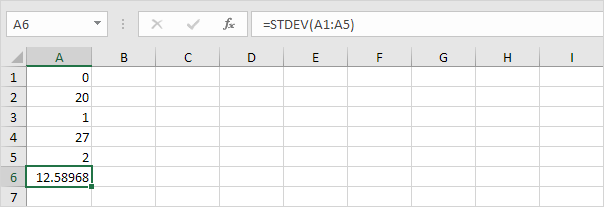
Explication: les chiffres sont répartis. En conséquence, les chiffres ont un écart élevé.

STDEV.P

La fonction STDEV.P (P représente la population) dans Excel calcule l’écart-type sur la base de l’ensemble de la population. Par exemple, vous enseignez un groupe de 5 étudiants. Vous avez les résultats des tests de tous les élèves. La population entière se compose de 5 points de données. La fonction STDEV.P utilise la formule suivante:

Formula of the Standard Deviation Based on the Entire Population

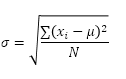
Dans cet exemple, x ~ 1 ~ = 5, x ~ 2 ~ = 1, x ~ 3 ~ = 4, x ~ 4 ~ = 6, x ~ 5 ~ = 9, μ = 5 (moyenne), N = 5 ( nombre de points de données).

  1. Calculer la moyenne (μ).

Calculate the Mean

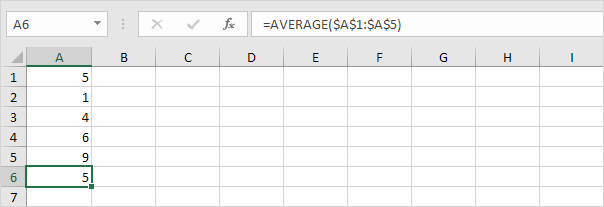
  1. Pour chaque numéro, calculer la distance à la moyenne.

Distance to the Mean

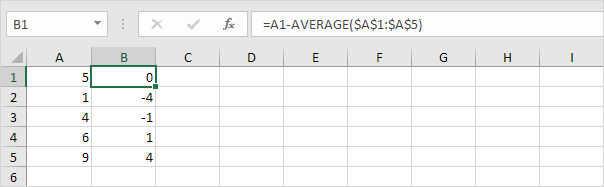
  1. Pour chaque numéro, carré cette distance.

Square of the Distance to the Mean

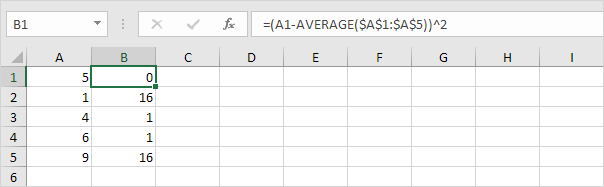
  1. Somme (Σ) ces valeurs.

Sum these Values

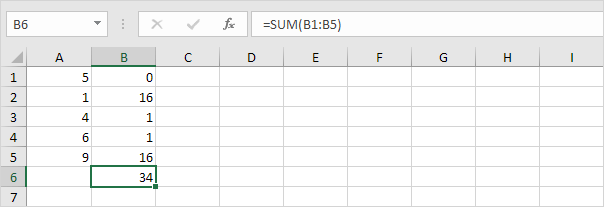
  1. diviser par le nombre de points de données (n = 5).

Divide by the Number of Data Points

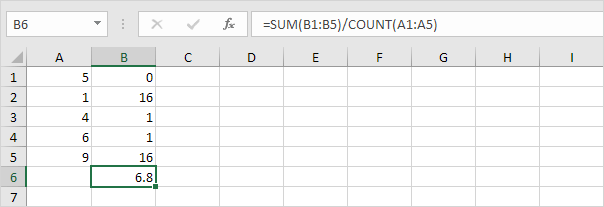
  1. Prendre le lien: / exemples racine carrée [racine carrée].

Standard Deviation Based on the Entire Population

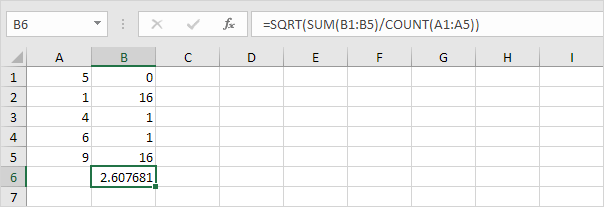
  1. Heureusement, la fonction STDEV.P dans Excel peut exécuter toutes ces étapes pour vous.

STDEV.P Function in Excel

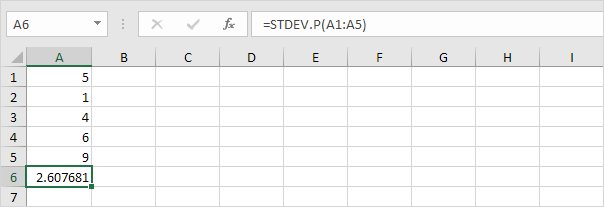
STDEV.S

La fonction STDEV.S (S représente l’échantillon) dans Excel estime l’écart-type sur la base d’un échantillon. Par exemple, vous enseignez un grand groupe d’étudiants. Vous avez seulement les résultats des tests de 5 étudiants.

La taille de l’échantillon est égal à 5. La fonction STDEV.S utilise la formule suivante:

Formula of the Standard Deviation Based on a Sample

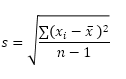
Dans cet exemple, x ~ 1 ~ = 5, x ~ 2 ~ = 1, x ~ 3 ~ = 4, x ~ 4 ~ = 6, x ~ 5 ~ = 9 (mêmes nombres que ci-dessus), X = 5 (échantillon moyenne), n = 5 (taille de l’échantillon).

  1. Répéter les étapes 1 à 5 ci-dessus, mais à l’étape 5 de division par n-1 au lieu de N.

Divide by n-1

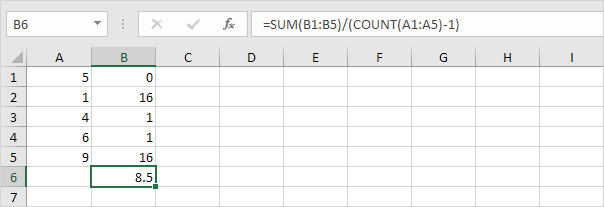
  1. Prenez le lien: / exemples racine carrée [racine carrée].

Standard Deviation Based on a Sample

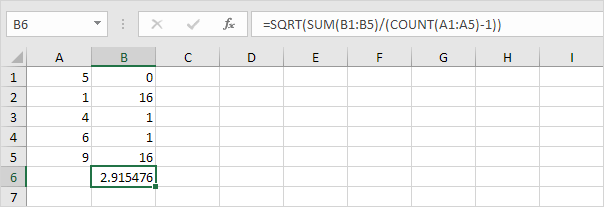
  1. Heureusement, la fonction STDEV.S dans Excel peut exécuter toutes ces étapes pour vous.

STDEV.S Function in Excel

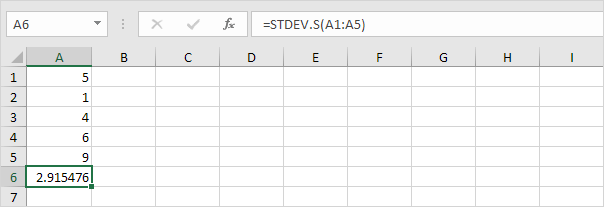
Note: pourquoi on divise par n – 1 au lieu de par n lorsque nous estimons l’écart-type sur la base d’un échantillon? Les états de correction de Bessel qui divisant par n-1 au lieu de par n donne une meilleure estimation de l’écart-type.