Transport problème dans Excel
Utilisez le solveur dans Excel pour trouver le nombre d’unités de chaque navire à l’usine à chaque client qui réduit le coût total.
qu’élaborer modèle
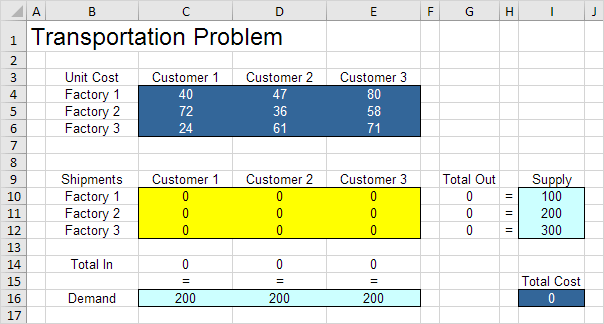
Le modèle que nous allons résoudre se présente comme suit dans Excel.
-
Pour formuler ce problème de transport, répondez aux trois questions suivantes.
\une. Quelles sont les décisions à prendre? Pour ce problème, nous avons besoin d’Excel pour savoir combien d’unités à expédier de chaque usine à chaque client.
\ B. Quelles sont les contraintes qui pèsent sur ces décisions? Chaque usine a une alimentation fixe et chaque client a une demande fixe.
\ C. Quelle est la mesure globale de la performance de ces décisions? La mesure globale de la performance est le coût total des livraisons, de sorte que l’objectif est de minimiser cette quantité.
-
Pour rendre le modèle plus facile à comprendre, nommez les plages suivantes.
|
Range Name |
Cells |
|
UnitCost |
C4:E6 |
|
Shipments |
C10:E12 |
|
TotalIn |
C14:E14 |
|
Demand |
C16:E16 |
|
TotalOut |
G10:G12 |
|
Supply |
I10:I12 |
|
TotalCost |
I16 |
-
Insérez les fonctions suivantes.
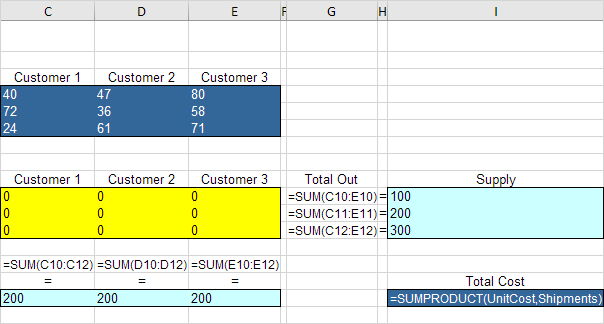
Explication: Les fonctions SUM calculer le total des marchandises transportées à partir de chaque usine (Total Out) à chaque client (Total In). Le coût total est égal à la SUMPRODUCT de UnitCost et livraisons.
Trial and Error
Avec cette formulation, il devient facile d’analyser toute solution d’essai.
Par exemple, si nous envoyons 100 unités de l’usine 1 au Client 1, 200 unités de l’usine 2 au Client 2, 100 unités de l’usine 3 à 1 et 200 unités client de l’usine 3 au Client 3, Total Out égale à l’offre et Total égaux Demande. Cette solution a un coût total de 27800.
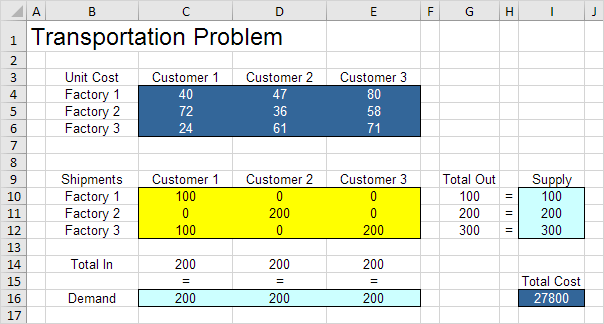
Il est pas nécessaire d’utiliser tâtonnement. Nous allons décrire ensuite comment Excel Solver peut être utilisé pour trouver rapidement la solution optimale.
Résoudre le modèle
Pour trouver la solution optimale, exécutez les étapes suivantes.
-
Dans l’onglet Données, dans le groupe Analyser, cliquez sur Solver.
Remarque: ne peut pas trouver le bouton Solver? Cliquez ici pour charger le complément Solver.
Entrez les paramètres du solveur (lire). Le résultat devrait être compatible avec l’image ci-dessous.
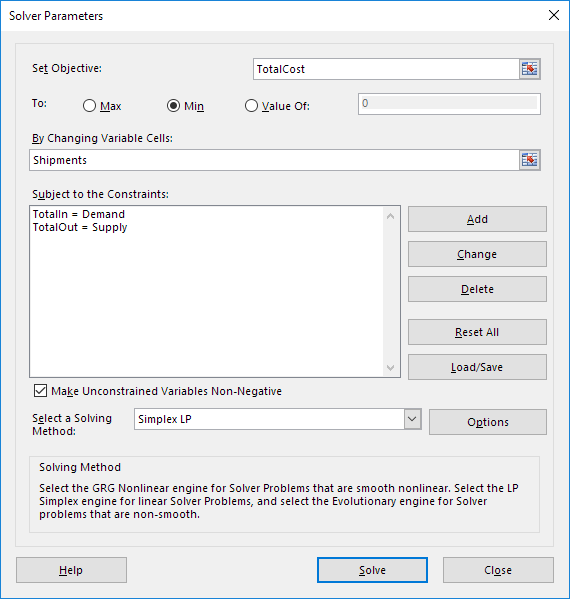
Vous avez le choix de taper les noms de plage ou en cliquant sur les cellules dans la feuille de calcul.
-
Entrez TotalCost pour l’objectif.
-
Cliquez sur Min.
-
Entrez les envois pour le changement des cellules variables.
-
Cliquez sur Ajouter pour saisir la contrainte suivante.
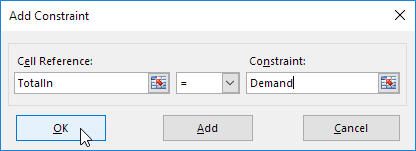
-
Cliquez sur Ajouter pour saisir la contrainte suivante.
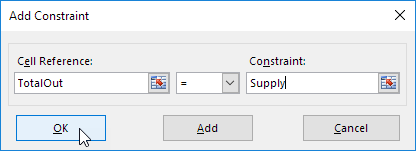
-
Cochez la case ‘Make Variables non sans contrainte négative’ et sélectionnez ‘Simplex LP’.
-
Enfin, cliquez sur Résoudre.
Résultat:
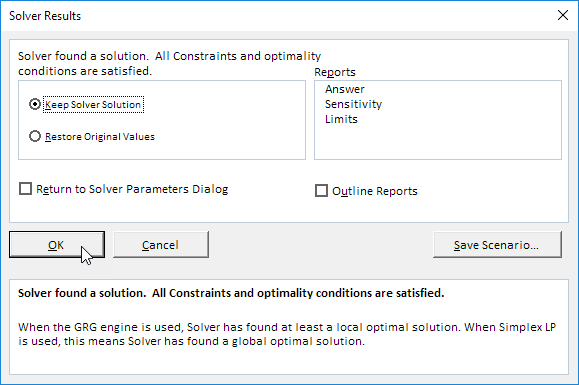
La solution optimale:
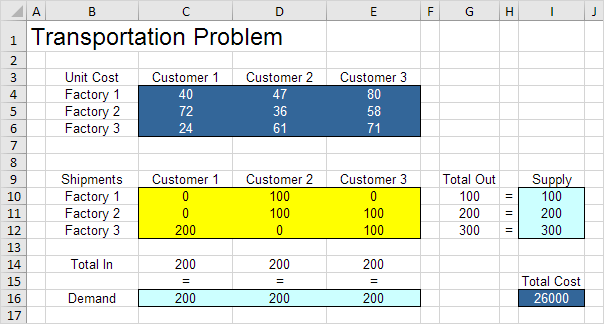
Conclusion: il est optimal pour expédier 100 unités de l’usine 1 au Client 2, 100 unités de l’usine 2 au Client 2, 100 unités de l’usine 2 au Client 3, 200 unités de l’usine 3 à 1 et 100 unités client de l’usine 3 au Client 3. Cette solution donne le coût minimum de 26000
Toutes les contraintes sont satisfaites.