Comment utiliser la fonction IMDIV dans Excel
Dans cet article, nous allons apprendre à utiliser la fonction IMDIV dans Excel.
Nombre COMPLEXE (en nombre) dans Excel dérivé pour un nombre mathématique ayant des coefficients réels et imaginaires. En mathématiques, nous l’appelons le coefficient de i ou j (iota).
i = √-1 La racine carrée d’un nombre négatif n’est pas possible, donc à des fins de calcul, √-1 est nommé comme imaginaire et l’appelle iota (i ou j). Pour le calcul d’un terme comme indiqué ci-dessous.
2 + √-25 = 2 + √-125 = 2 + √-125 = 2 + √-1 5 = 2 + 5i Cette équation ici est un nombre complexe (en nombre) ayant 2 parties différentes appelées partie réelle et partie imaginaire le coefficient de iota (i) qui vaut 5 est appelé partie imaginaire et l’autre partie 2 * est appelée partie réelle du nombre complexe.
Le nombre complexe (en nombre) est écrit au format X i * Y.
Division complexe d’un nombre complexe (X1 + iY1) & (X2 + i * Y2)
est donné par (X1 + iY1) / (X2 + i * Y2) = [(X1.X2 + Y1.Y2) + (Y1.X2 X1.Y2) i] / X2.X2 + Y2.Y2 Ici X & Y sont les coefficients de la partie réelle et imaginaire du nombre complexe (en nombre).
La fonction IMDIV renvoie la division du nombre complexe (en nombre)
ayant à la fois une partie réelle et imaginaire.
Syntaxe:
=IMDIV (inumber1 , inumber2)
inumber 1: Premier nombre complexe à diviser.
inumber 2: Second nombre complexe qui doit être divisé par le premier nombre complexe.
Comprenons cette fonction en l’utilisant dans un exemple.
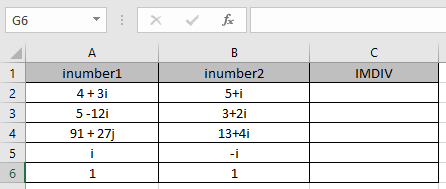
Ici, nous avons des valeurs où nous devons obtenir la division complexe du nombre complexe d’entrée (en nombre)
Utilisez la formule:
=IMDIV (A2, B2)
A2: numéro 1 (nombre complexe) fourni comme référence de cellule.
A2: numéro 2 (nombre complexe) fourni comme référence de cellule.
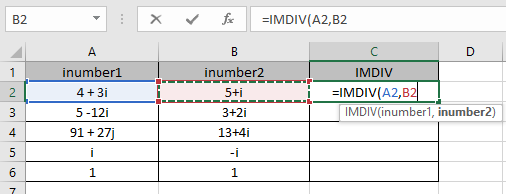
Les arguments de la fonction sont donnés comme référence de cellule.
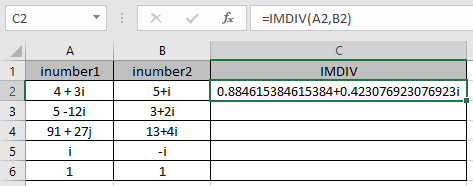
Comme vous pouvez le voir, le nombre complexe effectue l’opération de division.
La formulation mathématique est effectuée comme indiqué ci-dessous.
5 + i – (4 – i) = (5 – 4) + (i + i) = 1 + 2i Maintenant, copiez la formule dans les autres cellules restantes en utilisant la touche de raccourci Ctrl + D.
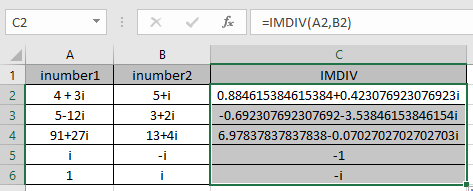
Le tableau présenté ici explique plus en détail les résultats
|
inumber1 |
inumber2 |
Real part 1 (X1) |
Imaginary part (Y1) |
Real part (X1) |
Imaginary part (Y2) |
|
i |
– i |
0 |
1 |
0 |
– 1 |
|
1 |
i |
1 |
0 |
0 |
1 |
Comme vous pouvez le voir, la formule de la fonction IMDIV donne des résultats très bien.
Remarque:
-
La formule renvoie le #NOMBRE! erreur si le nombre complexe n’a pas de minuscules i ou j (iota).
-
La formule renvoie la #VALEUR! Erreur si le nombre complexe n’a pas le format de nombre complexe correct.
J’espère que vous avez compris comment utiliser la fonction IMDIV et la cellule de référence dans Excel. Explorez plus d’articles sur les fonctions mathématiques d’Excel ici.
N’hésitez pas à formuler votre requête ou vos commentaires sur l’article ci-dessus.
Articles liés
lien: / maths-fonctions-excel-log10-function [Comment utiliser la fonction Excel LOG10]
lien: / excel-formule-et-fonction-comment-utiliser-la-fonction-imexp-dans-excel [Comment utiliser la fonction IMEXP dans Excel]
lien: / excel-formule-et-fonction-comment-utiliser-la-fonction-imconjugate-dans-excel [Comment utiliser la fonction IMCONJUGATE dans Excel]
lien: / fonctions-mathématiques-comment-utiliser-la-fonction-imargument-dans-excel [Comment utiliser la fonction IMARGUMENT dans Excel]
Articles populaires
link: / excel-generals-how-to-edit-a-dropdown-list-in-microsoft-excel [Edit a dropdown list]
lien: / conseils-formatage-conditionnel-avec-instruction-if [Si avec formatage conditionnel]
lien: / formules-logiques-si-fonction-avec-jokers [Si avec jokers]
lien: / lookup-formulas-vlookup-by-date-in-excel [Vlookup by date]