Comment utiliser la fonction Z.TEST dans Excel
Dans cet article, nous allons apprendre à utiliser la fonction Z.TEST dans Excel.
Qu’est-ce que le test d’hypothèse et comment utiliser Z -Test pour le test d’hypothèse? Dans les statistiques, le test d’hypothèse est utilisé pour trouver l’estimation de la moyenne pour l’ensemble de données de population en utilisant la fonction de distribution différente basée sur la partie de l’ensemble de données de population appelée ensemble de données échantillon. Une hypothèse statistique, parfois appelée analyse de données de confirmation, est une hypothèse testable en observant un processus modélisé via un ensemble de variables aléatoires. Il existe deux types d’hypothèses. L’une est l’hypothèse nulle qui est l’énoncé revendiqué et l’autre est l’hypothèse alternative qui est juste à l’opposé de l’hypothèse nulle. Par exemple, si nous disons que la limite maximale de plomb dans un paquet maggi ne doit pas dépasser 225 ppm (parties par million) et que quelqu’un prétend qu’il y a plus de limite fixe que l’hypothèse nulle (notée U ~ 0 ~) et l’hypothèse alternative (notée par U ~ a ~)
U ~ 0 ~ = la teneur en plomb dans le paquet maggi est supérieure ou égale à 225 ppm. U ~ a ~ = la teneur en plomb du paquet maggi est inférieure à 225 ppm.
L’hypothèse ci-dessus est donc un exemple de test unilatéralement car la situation sous-jacente se situe dans le côté droit de la courbe de distribution.
Si la situation sous-jacente se situe du côté gauche, cela s’appellerait un test unilatéral à gauche. Prenons un autre exemple qui illustre un test unilatéral. Par exemple, si selina dit qu’elle peut faire 60 pompes en moyenne. Maintenant, vous pourriez douter de cette déclaration et essayer de faire l’hypothèse de la situation en terme de statistiques, alors l’hypothèse nulle et alternative est énoncée ci-dessous U ~ 0 ~ = selina peut faire 60 pompes U ~ a ~ = selina ne peut pas faire 60 pompes Ceci est un deux – test abrégé où la situation sous-jacente se situe des deux côtés de la déclaration revendiquée. Ces tests en queue affectent le résultat des statistiques. Alors choisissez soigneusement l’hypothèse nulle et alternative.
Z – Test Un test Z est un test statistique pour lequel la distribution de la statistique de test sous l’hypothèse nulle peut être approchée par une distribution normale. Le test Z teste la moyenne d’une distribution dans laquelle nous connaissons déjà la variance de la population. En raison du théorème de limite central, de nombreuses statistiques de test sont à peu près normalement distribuées pour les grands échantillons. La statistique de test est supposée avoir une distribution normale telle que l’écart type doit être connu pour qu’un test z précis soit effectué. Par exemple, un investisseur souhaite tester si le rendement quotidien moyen d’une action est supérieur à 1% peut être évalué à l’aide du test Z. Une statistique Z ou un score Z * est un nombre représentant le nombre d’écarts types au-dessus ou en dessous de la population moyenne d’un score dérivé d’un test Z. Mathématiquement, nous décidons d’abord l’hypothèse nulle et calculons le score Z pour la distribution en utilisant la formule.
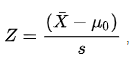
Ici X (avec une barre) est la moyenne du tableau d’échantillons U ~ 0 ~ est la moyenne estimée de la population s est l’écart type où s est égal à std / (n) ^ 1/2 ^ (où n est la taille de l’échantillon) .
Comme indiqué ci-dessus, le test Z suit la distribution normale standard. Donc mathématiquement dans Excel, il suit la formule suivante.
Z.TEST (tableau, x, sigma) = 1- Norm.S.Dist ((Moyenne (tableau) – x) / (sigma / (n) ^ 1/2 ^), TRUE)
ou lorsque sigma est omis:
Z.TEST (tableau, x) = 1- Norm.S.Dist ((Moyenne (tableau) – x) / (STDEV (tableau) / (n) ^ 1/2 ^), TRUE)
où x est la moyenne de l’échantillon MOYENNE (tableau), et n est COUNT (tableau).
Apprenons à faire le test Z en utilisant la fonction Z.TEST pour calculer la relation entre les deux ensembles de données donnés (réel et observé).
Fonction Z.TEST dans Excel
La fonction Z.TEST renvoie la probabilité que la moyenne de l’échantillon soit supérieure à la moyenne des observations dans l’ensemble de données (tableau). La fonction prend les arguments suivants.
Z.TEST Syntaxe de la fonction pour une probabilité de queue:
|
=Z.TEST ( array , x , [sigma] ) |
La fonction peut également être utilisée pour commuter la probabilité bilatérale.
Z.TEST Syntaxe de la fonction pour une probabilité de queue:
|
=2 * MIN(Z.TEST ( array , x , [sigma] ), 1-Z.TEST ( array , x , [sigma] ) ) |
array: distribution des données d’échantillon x: valeur pour laquelle le test z est évalué [sigma] *: [facultatif] Écart type (connu) de la population. S’il est omis, l’écart type de l’échantillon est utilisé.
Exemple:
Tout cela peut être difficile à comprendre. Comprenons comment utiliser la fonction à l’aide d’un exemple. Ici, nous avons un exemple de jeu de données Sales et nous devons trouver la probabilité du test Z pour la moyenne de population hypothétique donnée en supposant un test unilatéral.
Utilisez la formule:
|
= Z.TEST( A2:A9 , C3 ) |
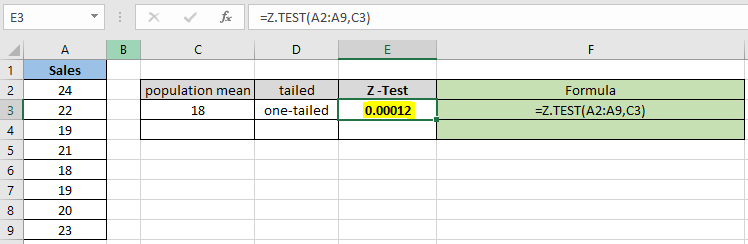
La valeur de probabilité est décimale, vous pouvez donc convertir la valeur en pourcentage en changeant le format de la cellule en pourcentage.
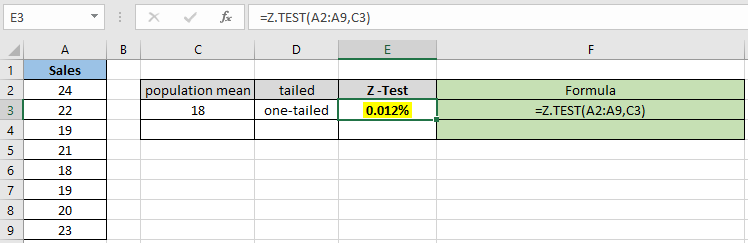
Comme vous pouvez le voir, la valeur de probabilité pour la moyenne de population hypothétique 18 est de 0,012% pour la distribution unilatérale. Calculez maintenant la probabilité en supposant deux distributions à queue ayant les mêmes paramètres.
Utilisez la formule:
|
= 2 * MIN( Z.TEST(A2:A9,C4) , 1 – Z.TEST(A2:A9,C4) ) |
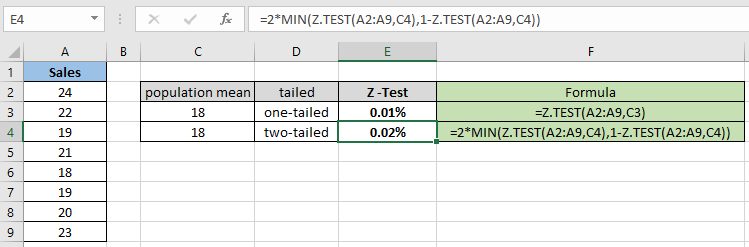
Pour la distribution bilatérale, la probabilité est doublée pour le même échantillon de données. Il est donc nécessaire de vérifier l’hypothèse nulle et l’hypothèse alternative. Calculez maintenant la probabilité pour les différentes moyennes de population hypothétiques et une distribution unilatérale.
Utilisez la formule:
|
= Z.TEST( A2:A9 , C5 ) |
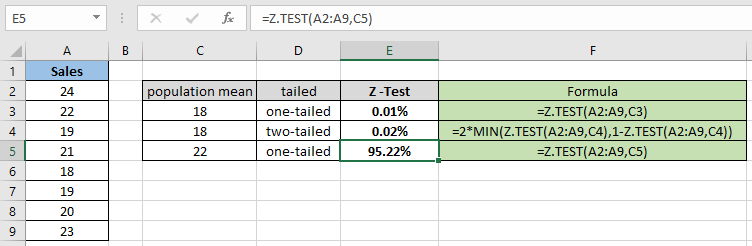
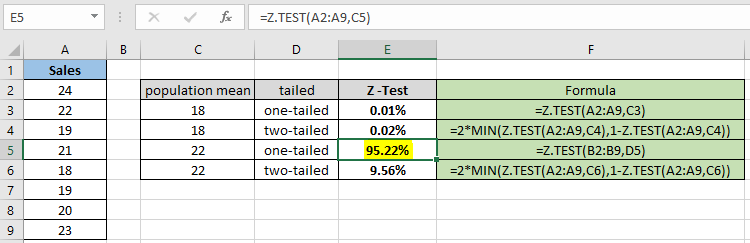
Comme vous pouvez le voir, la valeur de probabilité pour la moyenne hypothétique de la population 22 est de 95,22% pour la distribution unilatérale. Calculez maintenant la probabilité en supposant deux distributions à queue ayant les mêmes paramètres.
Utilisez la formule:
|
= 2 * MIN( Z.TEST(A2:A9,C6) , 1 – Z.TEST(A2:A9,C6) ) |
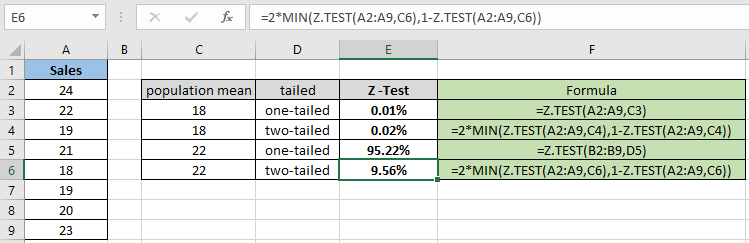
Comme vous pouvez différer de l’instantané ci-dessus, la valeur de probabilité diminue lors du calcul de la distribution bilatérale. La fonction renvoie 9,56% pour la moyenne hypothétique de la population 22.
Z.TEST représente la probabilité que la moyenne de l’échantillon soit supérieure à la valeur observée MOYENNE (tableau), lorsque la moyenne de la population sous-jacente est 0. À partir de la symétrie de la distribution normale, si MOYENNE (tableau) <x, Z.TEST sera renvoie une valeur supérieure à 0,5.
Voici toutes les notes d’observation utilisant la fonction Z.TEST dans Excel
Remarques:
-
La fonction ne fonctionne qu’avec des nombres. Si l’argument moyenne ou sigma de la population n’est pas numérique, la fonction renvoie #VALUE! Erreur.
-
La valeur en décimal ou la valeur en pourcentage est la même valeur dans Excel.
Convertissez la valeur en pourcentage, si nécessaire.
-
La fonction renvoie #NOMBRE! Erreur, si l’argument sigma est 0.
-
La fonction renvoie # N / A! Erreur si le tableau fourni est vide.
-
La fonction renvoie # DIV / 0! Erreur, .. Si l’écart type du tableau est 0 et que l’argument sigma est omis.
-
Si le tableau ne contient qu’une seule valeur.
-
J’espère que cet article sur Comment utiliser la fonction Z.TEST dans Excel est explicatif. Trouvez plus d’articles sur les formules statistiques et les fonctions Excel associées ici. Si vous avez aimé nos blogs, partagez-les avec vos amis sur Facebook. Et vous pouvez également nous suivre sur Twitter et Facebook. Nous serions ravis de vous entendre, faites-nous savoir comment nous pouvons améliorer, compléter ou innover notre travail et le rendre meilleur pour vous. Écrivez-nous à [email protected].
Articles liés:
link: / statistics-formules-how-to-use-t-test-function-in-excel [Comment utiliser la fonction Excel T TEST dans Excel]: Le T.TEST est utilisé pour déterminer la confiance d’une analyse. Mathématiquement, il permet de savoir si la moyenne des deux échantillons est égale ou non. T.TEST est utilisé pour accepter ou rejeter l’hypothèse nulle.
link: / statistics-formules-how-to-use-excel-f-test-function [Comment utiliser la fonction F.TEST d’Excel dans Excel]: La fonction F.TEST est utilisée pour calculer la statistique F de deux échantillons dans excel en interne et renvoie la probabilité bilatérale de la statistique F sous l’hypothèse nulle.
link: / statistiques-formules-comment-utiliser-la-fonction-devsq-dans-excel [Comment utiliser la fonction DEVSQ dans Excel]: La fonction DEVSQ est une fonction statistique intégrée pour calculer la somme des carrés écarts par rapport à la moyenne ou à la moyenne de la plage de valeurs de données fournies.
link: / statistics-formulas-how-to-use-excel-normdist-function [Comment utiliser Excel NORM.DIST Function]: Calcule le score Z pour la distribution cumulative normale pour les valeurs pré-spécifiées en utilisant la fonction NORMDIST dans Exceller.
link: / statistics-formules-how-to-use-excel-norm-inv-function [Comment utiliser Excel NORM.INV Function]: Calculez l’inverse du score Z pour la distribution cumulative normale pour la probabilité pré-spécifiée valeurs à l’aide de la fonction NORM.INV dans Excel.
lien: / excel-formules-financières-comment-calculer-l’écart-type-dans-Excel [Comment calculer l’écart-type dans Excel]: * Pour calculer l’écart type, nous avons différentes fonctions dans Excel. L’écart type est la racine carrée de la valeur de la variance, mais il en dit plus sur l’ensemble de données que sur la variance.
link: / statistics-formules-excel-var-function [Comment utiliser la fonction VAR dans Excel]: Calculez la variance de l’échantillon de données dans Excel en utilisant la fonction VAR dans Excel.
Articles populaires:
link: / tips-if-condition-in-excel [Comment utiliser la fonction IF dans Excel]: L’instruction IF dans Excel vérifie la condition et renvoie une valeur spécifique si la condition est TRUE ou renvoie une autre valeur spécifique si FALSE .
link: / formulas-and-functions-introduction-of-vlookup-function [Comment utiliser la fonction RECHERCHEV dans Excel]: C’est l’une des fonctions les plus utilisées et les plus populaires d’Excel qui est utilisée pour rechercher des valeurs dans différentes plages et feuilles. lien: / excel-formule-et-fonction-excel-sumif-function [Comment utiliser la fonction SUMIF dans Excel]: Ceci est une autre fonction essentielle du tableau de bord. Cela vous aide à résumer les valeurs sur des conditions spécifiques.
link: / tips-countif-in-microsoft-excel [Comment utiliser la fonction COUNTIF dans Excel]: Comptez les valeurs avec des conditions en utilisant cette fonction étonnante. Vous n’avez pas besoin de filtrer vos données pour compter des valeurs spécifiques. La fonction Countif est indispensable pour préparer votre tableau de bord.