Ci-dessous, nous examinerons un programme dans Excel VBA qui résout un petit exemple d’un problème de havresac.

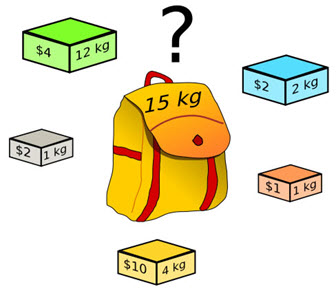
Définition: Soit un ensemble d’éléments, chacun ayant un poids et une valeur, déterminer les éléments à inclure dans une collection de telle sorte que la valeur totale est aussi grande que possible et le poids total est inférieur à une limite donnée.

Elle tire son nom du problème rencontré par quelqu’un qui est contraint par un havresac de taille fixe et doit le remplir avec les éléments les plus utiles.

Exemple: 5 éléments avec des poids, des valeurs et limite aussi donnés.

Knapsack Problem Image

Dans Excel ce problème se présente comme suit:

Knapsack Problem Example

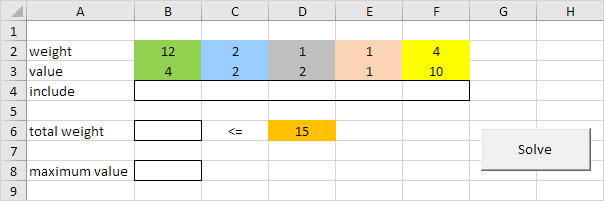
  1. Tout d’abord, nous déclarons cinq variables de type double avec des noms limite, le poids, la valeur, et MaximumValue poids total.

Dim limit As Double, weight As Double, value As Double, totalWeight As Double, maximumValue As Double

  1. Ensuite, nous déclarons cinq variables de type entier avec des noms i, j, k, l, m.

Dim i, j, k, l, m As Integer

  1. Nous initialisons deux variables. Nous initialisons la limite variable avec la valeur de la cellule D6. Nous initialisons la MaximumValue variable avec la valeur 0.

limit = Range("D6").value

maximumValue = 0

  1. Ensuite, nous vérifions chaque solution possible. Nous pouvons soit inclure un élément (1) ou à laisser sur (0). Nous commençons 5 Pour les boucles suivantes. L’un pour chaque élément.

For i = 0 To 1

For j = 0 To 1

For k = 0 To 1

For l = 0 To 1

For m = 0 To 1

  1. Nous calculons le poids et la valeur d’une solution possible.

weight = 12  i + 2  j + 1  k + 1  l + 4  m

value = 4  i + 2  j + 2  k + 1  l + 10  m

  1. Seulement si la valeur est supérieure à MaximumValue et le poids est inférieur à la limite, nous avons trouvé une nouvelle meilleure solution.

If value > maximumValue And weight <= limit Then

  1. Si cela est vrai, nous écrivons la nouvelle solution à la ligne 4, le poids et la valeur de poids total à MaximumValue.

Range("B4").value = i

Range("C4").value = j

Range("D4").value = k

Range("E4").value = l

Range("F4").value = m

totalWeight = weight

maximumValue = value

  1. Ne pas oublier de fermer l’instruction if.

End If

  1. Ne pas oublier de fermer les 5 boucles pour Suivant.

Next m

Next l

Next k

Next j

Next i

Excel VBA vérifie chaque solution possible de cette façon et par conséquent la solution optimale apparaît dans la ligne 4. Rappelez-vous, 1 signifie que nous avons inclus un élément, 0 signifie que nous laissons sortir.

  1. Enfin, écrire et MaximumValue poids total de la solution optimale pour la cellule B6 et B8 respectivement.

Range("B6").value = totalWeight

Range("B8").value = maximumValue

  1. Tester le programme.

Résultat:

Knapsack Problem Result

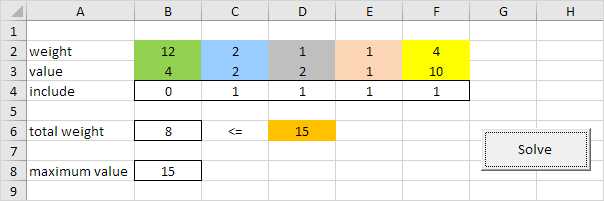
Conclusion: cette optimal pour inclure les quatre derniers éléments avec une valeur maximale de 15. Cette solution avec un poids total de 2 + 1 + 1 + 4 = 8 ne dépasse pas la limite de 15.

Remarque: en faisant la variable de poids et les valeurs que vous pouvez résoudre tout problème de cette taille de sac (voir fichier Excel téléchargeable).