Excel에서 표준 편차
이 페이지는 어떻게 Excel에서 STDEV.S 기능을 사용하여 샘플을 기준으로 표준 편차를 추정하기 STDEV.P의 Excel의 기능을 사용하여 전체 모집단을 기준으로 표준 편차를 계산하는 방법을 설명합니다.
[[what-is-standard-deviation?]]
=== 표준 편차는 무엇입니까?
표준 편차는 숫자가 평균에서 얼마나 멀리 알려주는 숫자입니다.
-
예를 들어, 아래의 숫자 (10)의 평균 (평균)가
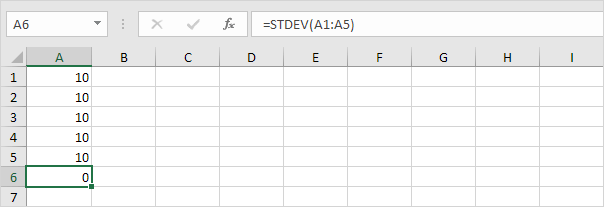
설명 : 숫자가 전혀 변화가 없습니다 의미 동일합니다. 그 결과, 번호는 0의 표준 편차를 가지고있다.
STDEV 함수는 오래된 기능입니다. Microsoft Excel에서이 동일한 결과를 생성하는 새로운 STEDV.S 기능을 사용하는 것이 좋습니다.
-
숫자는 아래도 10의 (평균) 평균이
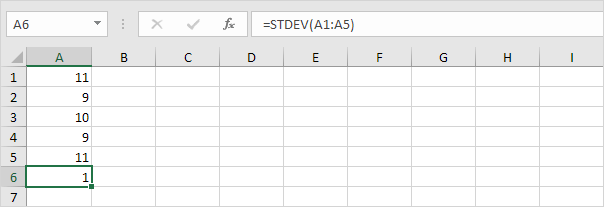
설명 : 숫자가 평균에 가깝습니다. 그 결과, 번호가 낮은 표준 편차를 가지고있다.
-
숫자는 아래도 10의 (평균) 평균이
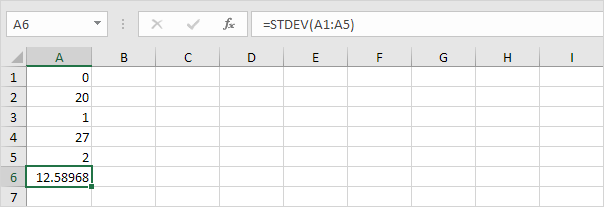
설명 : 숫자가 퍼져있다. 그 결과, 숫자는 높은 표준 편차를 가지고있다.
STDEV.P
Excel에서 STDEV.P 기능합니다 (P는 인구의 약자) 전체 모집단을 기준으로 표준 편차를 계산합니다. 예를 들어, 5 명 학생의 그룹을 가르치고 있습니다. 당신은 모든 학생의 성적을 가지고있다. 전체 인구는 5 개 데이터 포인트로 구성되어 있습니다. STDEV.P 함수는 다음 식을 사용
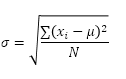
이 예에서, X ~ = 5 1, X ~ = 1 (2), X ~ = 4 3 X ~ = 6 (4), X ~ = 9, μ = 5 (평균) 5, N = 5 ( 데이터 포인트의 수).
계산 1. 평균 (μ).
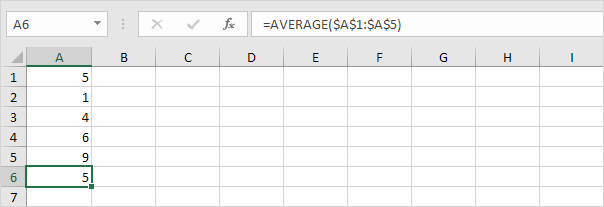
각 번호 2. 상기 평균 거리를 계산한다.
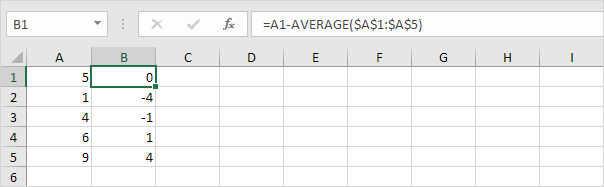
-
각 번호의 경우,이 거리를 광장.
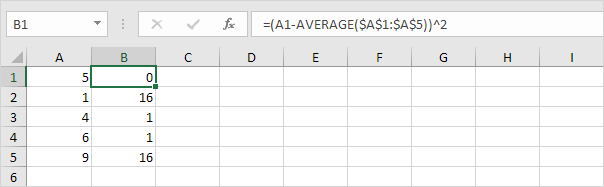
-
합계 (Σ)이 값.
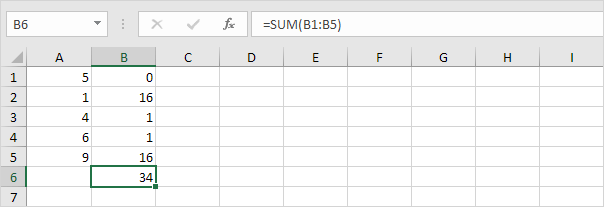
데이터 지점 (N = 5)의 수에 의해 제 나눈다.
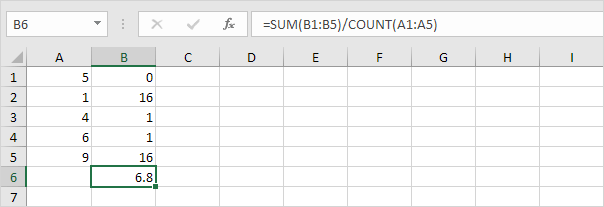
은`링크를 타고 6 : / 예 – 제곱근 [제곱근]`.
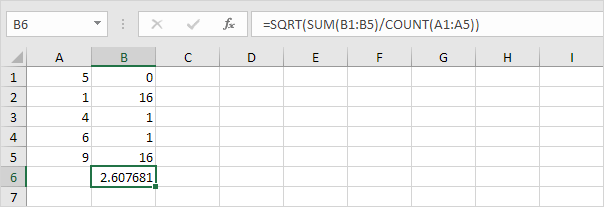
-
다행히, Excel에서 STDEV.P 기능은 당신을 위해 모든 단계를 실행할 수 있습니다.
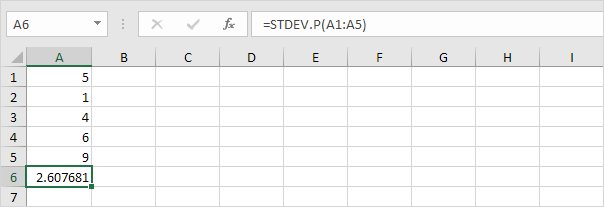
STDEV.S
Excel에서 STDEV.S 기능합니다 (S가 샘플을 의미) 표본을 기준으로 표준 편차를 추정하고있다. 예를 들어, 학생들의 큰 그룹을 가르치고 있습니다. 당신은 5 명의 학생의 성적을 가지고있다.
샘플 크기는 제 STDEV.S 함수는 다음 식을 사용 같다 :
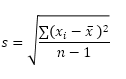
이 예에서, X ~ = 5 1, X ~ = 1 (2), X ~ = 4 3 X ~ = 6 (4), X ~ 5 ~ = 9 (동일한 번호 위 등), X = 5 (샘플 평균), N = 5 (샘플 크기).
-
상기 반복하지만, N-1 대신에 N으로 나누어 5 단계에서, 단계 1 내지 5
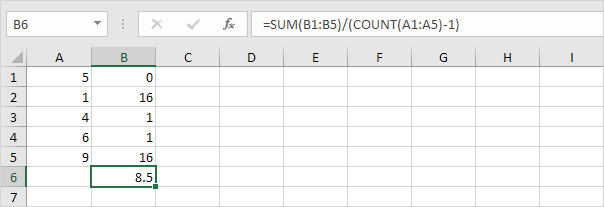
은`링크를 타고 2 : / 예 – 제곱근 [제곱근]`.
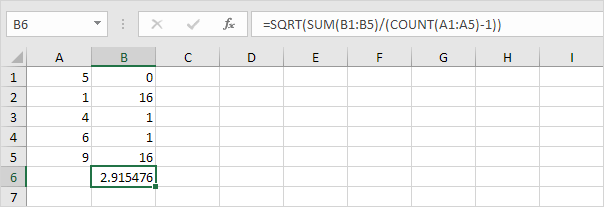
-
다행히, Excel에서 STDEV.S 기능은 당신을 위해 모든 단계를 실행할 수 있습니다.
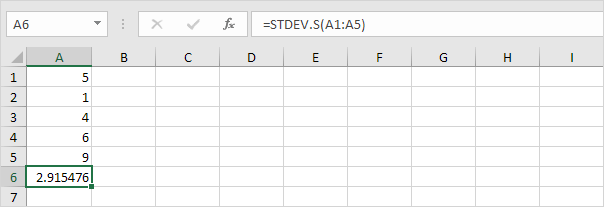
참고 : 우리가 왜 n으로 나누어 않는다 – 1 대신하여 N 우리는 표본을 기준으로 표준 편차를 추정 할 때? 베셀의 보정 상태는 N-1 대신에 N으로 분할하는 표준 편차의 더 나은 추정을 준다.