Cajas y bigotes parcela en Excel
En este ejemplo se le enseña cómo crear un diagrama de cajas y bigotes en Excel. Una caja y bigotes gráfica muestra el valor mínimo, primero enlace : / ejemplos-percentiles-cuartiles [cuartil], la mediana, el tercer cuartil y el valor máximo de un conjunto de datos.
simple cajas y bigotes parcela
-
Por ejemplo, seleccione el rango A1: A7.
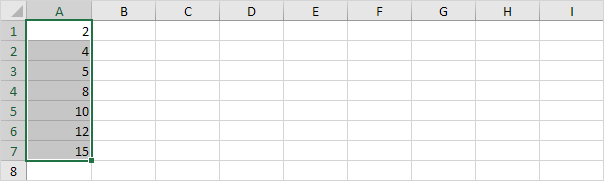
Nota: usted no tiene que ordenar los puntos de datos de menor a mayor, pero nos ayudará a entender la caja y bigotes parcela.
-
En la ficha Insertar, en el grupo Gráficos, haga clic en el símbolo gráfico estadístico.

-
Haga clic en cajas y bigotes.
Resultado:
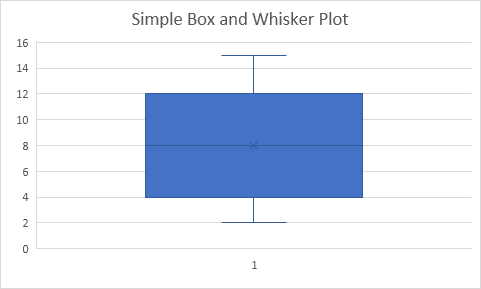
Explicación: la línea media de la caja representa la mediana o número del medio (8). La x en el cuadro representa la media (también 8 en este ejemplo). Los divide la mediana del conjunto de datos en un medio inferior \ {2, 4, 5} y una mitad superior \ {10, 12, 15}. La línea inferior de la caja representa la mediana de la mitad inferior o primera cuartil (4). La línea superior de la caja representa la mediana de la mitad superior o tercera cuartil (12). Los bigotes (líneas verticales) se extienden desde los extremos de la caja para el valor mínimo (2) y el valor máximo (15).
Los valores atípicos
-
Por ejemplo, seleccione el rango A1: A11.
Nota: la mediana o media de número (8) divide el conjunto de datos en dos mitades: \ {1, 2, 2, 4, 5} y \ {10, 12, 15, 18, 35}. La primera cuartil (Q ~ 1 ~) es la mediana de la primera mitad. Q ~ 1 ~ = 2. El tercero cuartil (Q ~ 3 ~) es la mediana de la segunda mitad. Q ~ 3 ~ = 15.
-
En la ficha Insertar, en el grupo Gráficos, haga clic en el símbolo gráfico estadístico.

-
Haga clic en cajas y bigotes.

Resultado:
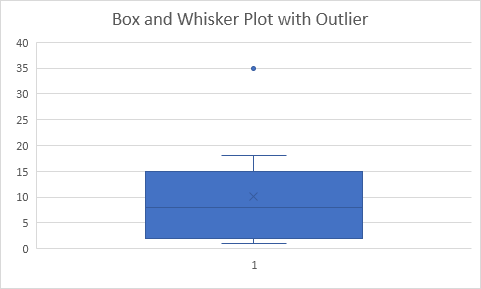
Explicación: el rango intercuartílico (IQR) se define como la distancia entre la primera cuartil y la tercera cuartil. En este ejemplo, IQR = Q ~ 3 ~ – Q ~ 1 ~ = 15 – 2 = 13. punto A de datos se considera un valor atípico si excede de una distancia de 1,5 veces el IQR por debajo de la primera cuartil (Q ~ 1 ~ – 1,5 IQR = 2 – 1,5 13 = -17,5) o 1,5 veces el IQR por encima de la tercera cuartil (Q ~ 3 ~ + 1,5 IQR = 15 + 1,5 13 = 34,5). Por lo tanto, en este ejemplo, 35 se considera un valor atípico. Como resultado, la parte superior de la barba se extiende hasta el valor más grande (18) dentro de este rango.
-
Cambiar los últimos datos apuntan a 34.
Resultado:
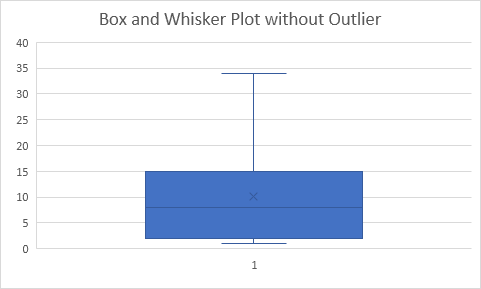
Explicación: todos los puntos de datos son entre -17,5 y 34,5. Como resultado, los bigotes se extienden hasta el valor mínimo (2) y el valor máximo (34).
Box Cálculos Trazar
La mayoría de las veces, puede no se puede determinar con facilidad la primera y tercera cuartil cuartil sin realizar cálculos.
-
Por ejemplo, seleccione el número par de puntos de datos de abajo.
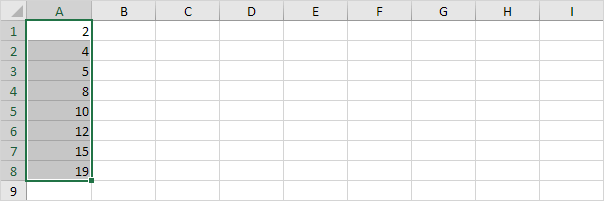
-
En la ficha Insertar, en el grupo Gráficos, haga clic en el símbolo gráfico estadístico.

-
Haga clic en cajas y bigotes.

Resultado:
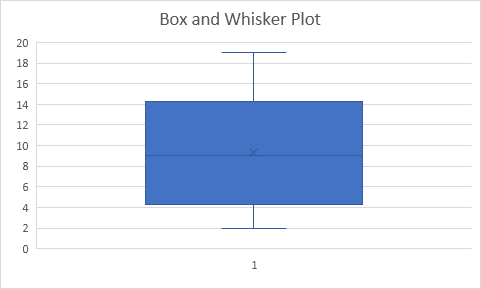
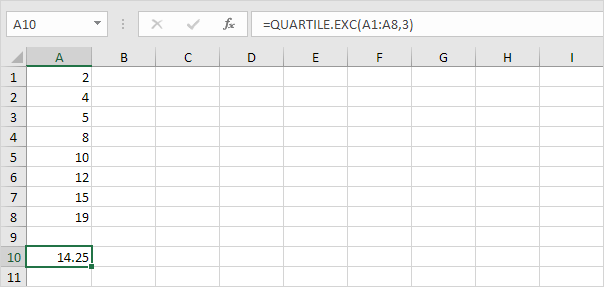
Explicación: Excel utiliza la función QUARTILE.EXC para calcular la primera cuartil (Q ~ 1 ~), segundo cuartil (Q ~ 2 ~ o mediana) y 3º cuartil (Q ~ 3 ~).
Esta función interpola entre dos valores para calcular un cuartil.
En este ejemplo, n = 8 (número de puntos de datos).
-
Q ~ 1 ~ = 1/4 (n + 1) -ésimo valor = 1/4 (8 + 1) -ésimo valor = 2 1 / cuarto valor = 4 + 1/4 (5-4) = 4 1/4 . Usted puede verificar este número utilizando la función QUARTILE.EXC o mirar la caja y bigotes parcela.
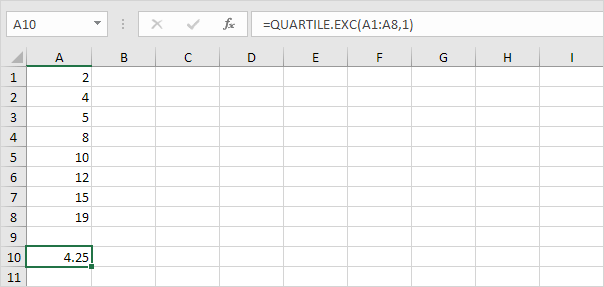
-
Q ~ 2 ~ = 1/2 (N + 1) -ésimo valor = 1/2 (8 + 1) -ésimo valor = 4 1 / valor 2 Tes = 8 + 1/2 (10-8) = 9. Esto hace sentido, la mediana es el promedio de los dos números centrales.
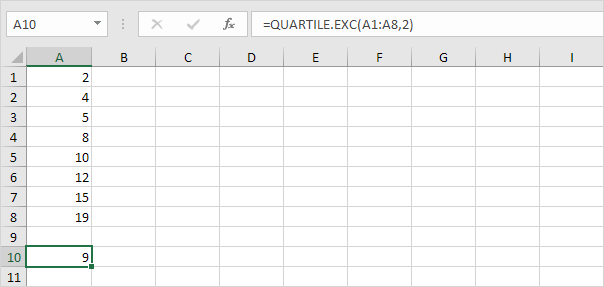
-
Q ~ 3 ~ = 3/4 (n + 1) -ésimo valor = 3/4 (8 + 1) -ésimo valor = 6 3 / cuarto valor = 12 + 3/4 * (15-12) = 14 1 / 4. Una vez más, se puede verificar este número utilizando la función QUARTILE.EXC o mirar la caja y bigotes parcela.