Análisis de regresión en Excel
R Square | Importancia F y los valores de p | enlace: #coefficients [] Coeficientes | enlace: [#residuals Residuales]
En este ejemplo se le enseña cómo realizar un análisis de regresión lineal en Excel y cómo interpretar la salida de resumen.
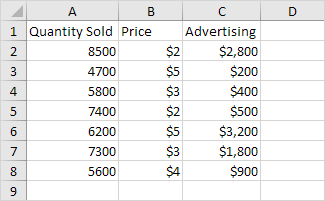
A continuación puede encontrar nuestros datos. La gran pregunta es: ¿hay una relación entre la cantidad vendida (salida) y el precio y publicidad (de entrada). En otras palabras: ¿se puede predecir Cantidad vendida si sabemos precio y la publicidad?
-
En la ficha Datos, en el grupo de análisis, haga clic en Análisis de datos.
Nota: no puede encontrar el botón de análisis de datos? Hacer clic para cargar las Herramientas para análisis complemento.
-
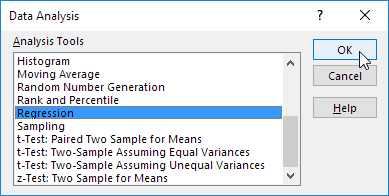
Seleccionar una regresión y haga clic en OK.
-
Seleccione el rango Y (A1: A8). Esta es la variable predictora (también llamada variable dependiente).
-
Seleccione el rango X (B1: C8). Estas son las variables explicativas (también llamadas variables independientes). Estas columnas tienen que ser adyacentes entre sí.
-
Revise las etiquetas.
-
Haga clic en el cuadro Rango de salida y seleccione la celda A11.
-
Revisar Residuos.
-
Haga clic en OK.
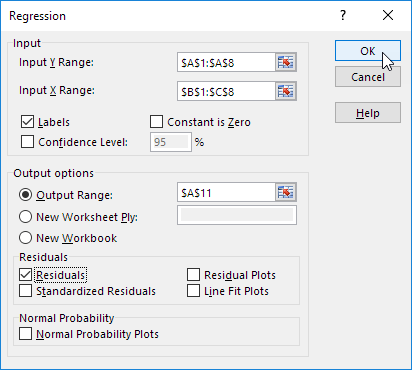
Excel produce la siguiente salida Resumen (redondeado a 3 cifras decimales).
R Square
R Square es igual a 0,962, que es un muy buen ajuste. 96% de la variación de la cantidad vendida se explica por las variables de precio y publicidad. Cuanto más cerca de 1, mejor es la línea de regresión (leyendo) se ajusta a los datos.
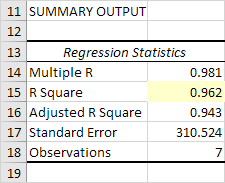
Importancia F y los valores de p
Para comprobar si los resultados son fiables (estadísticamente significativo), Importancia vistazo a F (0,001). Si este valor es inferior a 0,05, que estás bien.
Si Importancia F es mayor que 0,05, es probablemente mejor dejar de usar este conjunto de variables independientes. Eliminar una variable con un alto valor P (superior a 0,05) y vuelva a ejecutar la regresión hasta Importancia F cae por debajo de 0,05.
La mayoría o todos los valores de P deben estar por debajo por debajo de 0,05. En nuestro ejemplo, este es el caso. (0.000, 0.001 y 0.005).
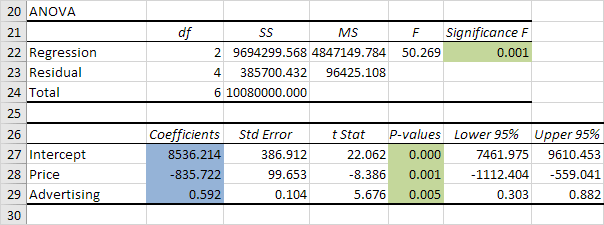
Coeficientes
La línea de regresión es: y = Cantidad vendida = 8536.214 -835.722 Precio + 0,592 Publicidad. En otras palabras, por cada unidad de aumento en el precio, Cantidad_Vendida disminuye con 835.722 unidades. Para cada unidad de aumento en la publicidad, Cantidad vendida aumenta con 0.592 unidades. Esta es una información valiosa.
También puede utilizar estos coeficientes de hacer un pronóstico. Por ejemplo, si el precio es igual a $ 4 y Publicidad es igual a $ 3000, usted podría ser capaz de lograr un Cantidad_Vendida de 8.536,214 -835.722 4 + 0,592 = 3,000 6970.
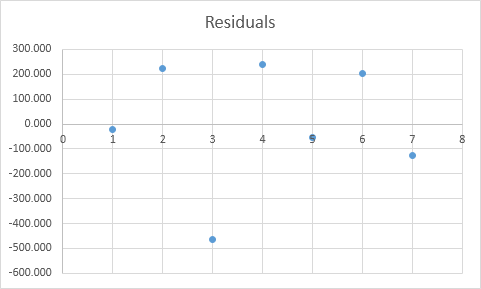
Residuales
Los residuos que muestran lo lejos que los puntos de datos reales son FOM los puntos de datos predichos (usando la ecuación). Por ejemplo, el primer punto de datos es igual a 8500. Usando la ecuación, el punto de datos predicho es igual a 8536.214 -835.722 2 + 0,592 2,800 = 8523.009, dando un residuo de 8500-8.523,009 = -23,009.
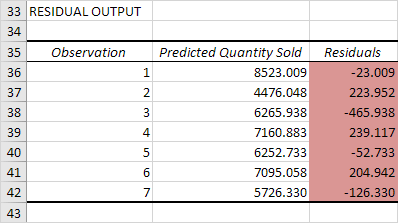
También puede crear un gráfico de dispersión de estos residuos.