Formule el modelo | Trial and Error | resolver el modelo

Utilizar el solucionador en Excel para encontrar la ruta más corta desde el nodo S al nodo T en una red no dirigida. Puntos de una red se denominan nodos (S, A, B, C, D, E y T). Líneas en una red se llaman arcos (SA, SB, SC, AC, etc).

Formular el Modelo

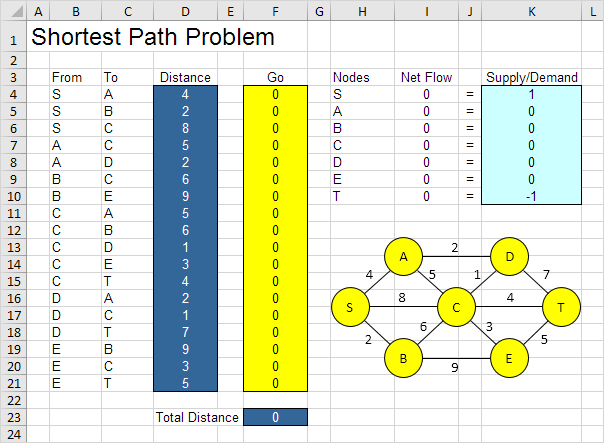
El modelo que se va a resolver el siguiente aspecto en Excel.

Shortest Path Problem in Excel

  1. Formular el problema del camino más corto, responda a las siguientes tres preguntas.

\un. ¿Cuáles son las decisiones que se harán? Para este problema, necesitamos Excel para averiguar si un arco se encuentra en la ruta más corta o no (Sí = 1, n = 0). Por ejemplo, si SB es parte de la ruta más corta, célula F5 es igual a 1. Si no es así, la celda F5 es igual a 0.

\segundo. ¿Cuáles son las limitaciones de estas decisiones? El flujo neto (Flujo de salida – Flujo de entrada) de cada nodo debe ser igual a la oferta / demanda. El nodo S sólo debe tener un arco de salida (flujo neto = 1). Nodo T sólo debe tener un arco entrante (flujo neto = -1). Todos los otros nodos deben tener un arco saliente y un arco entrante si el nodo está en el camino más corto (flujo neto = 0) o ningún flujo (flujo neto = 0).

\C. ¿Cuál es la medida global de rendimiento para estas decisiones? La medida global de la actuación es la distancia total de la ruta más corta, por lo que el objetivo es reducir al mínimo esta cantidad.

  1. Para hacer el modelo más fácil de entender, por nombrar los siguientes rangos.

Range Name

Cells

From

B4:B21

To

C4:C21

Distance

D4:D21

Go

F4:F21

NetFlow

I4:I10

SupplyDemand

K4:K10

TotalDistance

F23

  1. Inserte las siguientes funciones.

Insert Functions

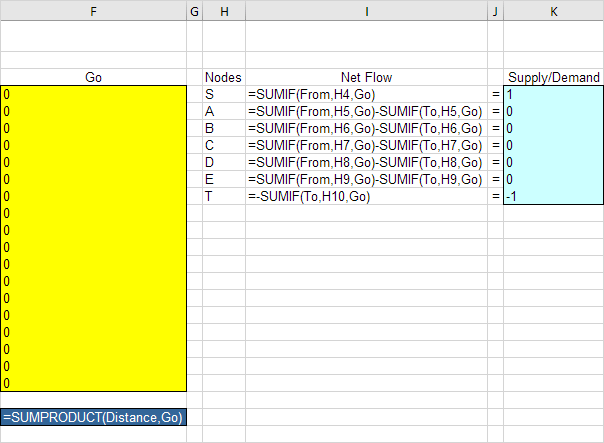
Explicación: El enlace: / ejemplos-función SUMIF [función SUMIF] funciones calcular el flujo neto de cada nodo. Para el nodo S, la función de cálculo SUMAR.SI suma los valores de la columna Go con una «S» en la columna De. Como resultado, sólo la celda F4, F5 o F6 puede ser 1 (un arco saliente). Para el nodo T, la función de cálculo SUMAR.SI suma los valores de la columna Go con una «T» en la columna A. Como resultado, sólo F15 celular, F18 o F21 pueden ser 1 (un arco entrante). Para todos los demás nodos, Excel busca en el De y columna. Distancia total es igual a la distancia de sumproduct and Go.

Ensayo y error

Con esta formulación, se hace fácil para analizar cualquier solución de prueba.

  1. Por ejemplo, el SBET camino tiene una distancia total de 16.

Trial Solution

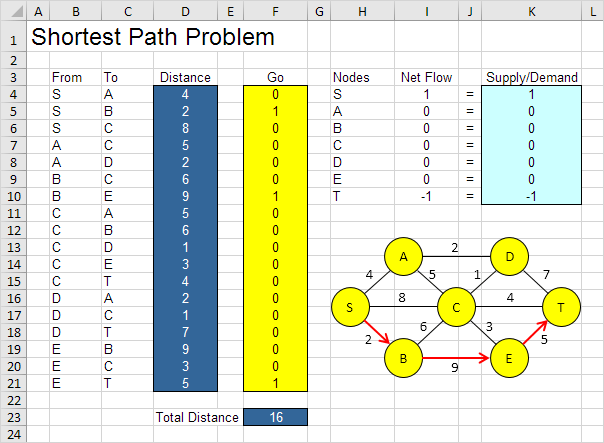
No es necesario el uso de ensayo y error. Vamos a describir a continuación cómo el Solver de Excel se puede utilizar para encontrar rápidamente la solución óptima.

resolver el modelo

Para encontrar la solución óptima, ejecutar los siguientes pasos.

  1. En la ficha Datos, en el grupo Analizar, haga clic en Solver.

Click Solver

Nota: no puede encontrar el botón Solver? Haga clic aquí para cargar el complemento Solver.

Introduzca los parámetros de Solver (leyendo). El resultado debe ser consistente con la imagen de abajo.

Solver Parameters

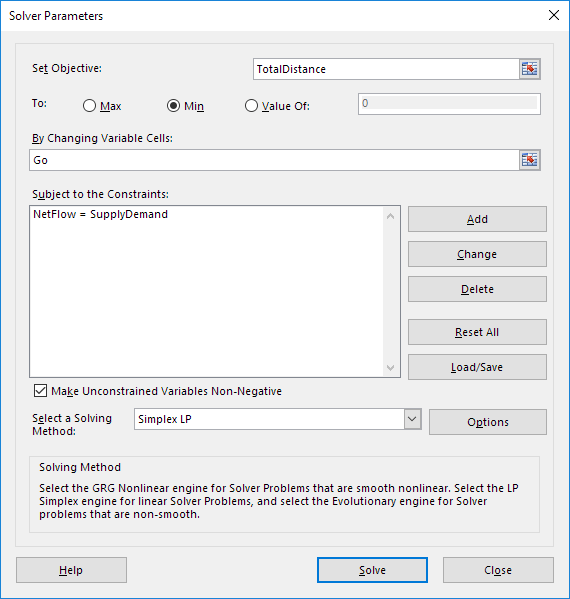
Usted tiene la opción de escribir los nombres de rango o haciendo clic en las celdas de la hoja de cálculo.

  1. Introduzca totalLa para el objetivo.

  2. Haga clic Min.

  3. Introduzca Ir para las células de variables cambiantes.

  4. Haga clic en Agregar para introducir la siguiente restricción.

Net Flow Constraint

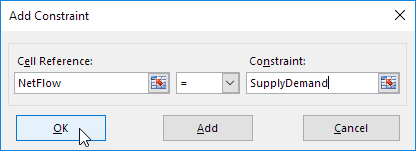
  1. Comprobar ‘Make variables sin restricciones no negativo’ y seleccione ‘Simplex LP’.

  2. Por último, haga clic en Resolver.

Resultado:

Solver Results

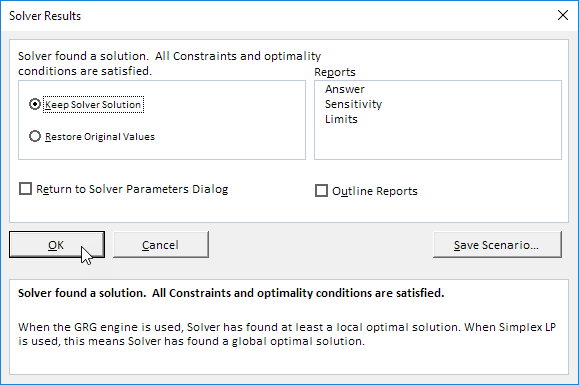
La solución óptima:

Shortest Path Problem Result

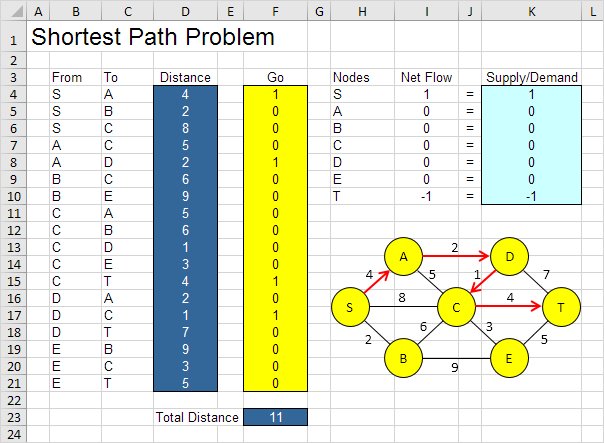
Conclusión: SADCT es el camino más corto con una distancia total de 11.