Cómo utilizar la función IM.DIV en Excel
En este artículo, aprenderemos cómo usar la función IMDIV en Excel.
Número COMPLEJO (inumber) en Excel derivado de números matemáticos que tienen coeficientes reales e imaginarios. En matemáticas lo llamamos coeficiente de i o j (iota).
i = √-1 La raíz cuadrada de un número negativo no es posible, por lo que para fines de cálculo, √-1 se nombra como imaginario y lo llama iota (i o j). Para el cálculo de algún término como se muestra a continuación.
2 + √-25 = 2 + √-125 = 2 + √-125 = 2 + √-1 5 = 2 + 5i Esta ecuación es un número complejo (en número) que tiene 2 partes diferentes llamadas parte real y parte imaginaria La El coeficiente de iota (i) que es 5 se llama parte imaginaria y la otra parte 2 * se llama parte real del número complejo.
El número complejo (en número) se escribe en formato X i * Y.
División compleja de un número complejo (X1 + iY1) & (X2 + i * Y2)
viene dado por (X1 + iY1) / (X2 + i * Y2) = [(X1.X2 + Y1.Y2) + (Y1.X2 X1.Y2) i] / X2.X2 + Y2.Y2 Aquí X e Y son los coeficientes de la parte real e imaginaria del número complejo (en número).
La función IMDIV devuelve la división del número complejo (en número)
teniendo parte tanto real como imaginaria.
Sintaxis:
=IMDIV (inumber1 , inumber2)
inumber 1: Primer número complejo que se va a dividir.
inumber 2: Segundo número complejo que se dividirá por el primer número complejo.
Entendamos esta función usándola en un ejemplo.
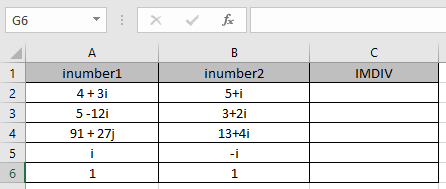
Aquí tenemos valores donde necesitamos obtener la división compleja del número complejo de entrada (en número)
Usa la fórmula:
=IMDIV (A2, B2)
A2: el número 1 (número complejo) se proporciona como referencia de celda.
A2: el número 2 (número complejo) se proporciona como referencia de celda.
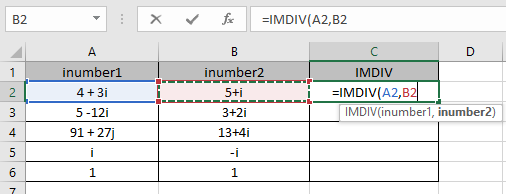
Los argumentos de la función se dan como referencia de celda.
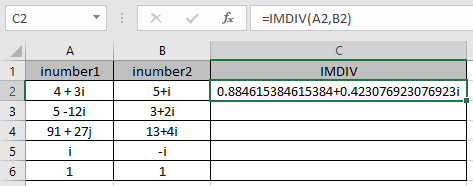
Como puede ver, el número complejo realiza la operación de división.
La formulación matemática se realiza como se muestra a continuación.
5 + i – (4 – i) = (5-4) + (i + i) = 1 + 2i Ahora copie la fórmula en las otras celdas restantes usando la tecla de método abreviado Ctrl + D.
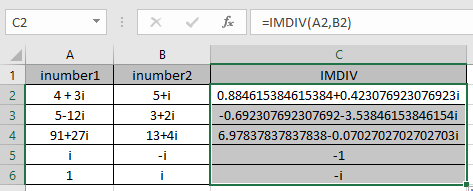
La tabla que se muestra aquí explica más sobre los resultados
|
inumber1 |
inumber2 |
Real part 1 (X1) |
Imaginary part (Y1) |
Real part (X1) |
Imaginary part (Y2) |
|
i |
– i |
0 |
1 |
0 |
– 1 |
|
1 |
i |
1 |
0 |
0 |
1 |
Como puede ver, la fórmula de la función IMDIV da buenos resultados.
Nota:
-
La fórmula devuelve el # ¡NUM! error si el número complejo no tiene i o j minúscula (iota).
-
La fórmula devuelve el # ¡VALOR! Error si el número complejo no tiene el formato de número complejo correcto.
Espero que haya entendido cómo usar la función IMDIV y la celda de referencia en Excel. Explore más artículos sobre funciones matemáticas de Excel aquí.
No dude en hacernos llegar sus consultas o comentarios sobre el artículo anterior.
Artículos relacionados
link: / funciones-matemáticas-excel-log10-function [Cómo usar la función LOG10 de Excel]
link: / excel-formula-and-function-how-to-use-the-imexp-function-in-excel [Cómo usar la función IMEXP en Excel]
link: / excel-formula-and-function-how-to-use-the-imconjugate-function-in-excel [Cómo usar la función IMCONJUGATE en Excel]
link: / funciones-matemáticas-cómo-usar-la-función-imargument-en-excel [Cómo usar la función IMARGUMENT en Excel]
Artículos populares
link: / excel-generals-how-to-edit-a-dropdown-list-in-microsoft-excel [Editar una lista desplegable]
link: / tips-conditional-formatting-with-if-statement [Si con formato condicional]
enlace: / fórmulas-lógicas-si-función-con-comodines [Si con comodines]
enlace: / lookup-formulas-vlookup-by-date-in-excel [Vlookup por fecha]