Débit maximal problème dans Excel
Utiliser le solveur dans Excel pour trouver le débit maximal à partir du noeud S au noeud T dans un réseau orienté. Les points dans un réseau sont appelés noeuds (S, A, B, C, D, E et T). Les lignes d’un réseau sont appelés arcs (SA, SB, SC, AC, etc.).
qu’élaborer modèle
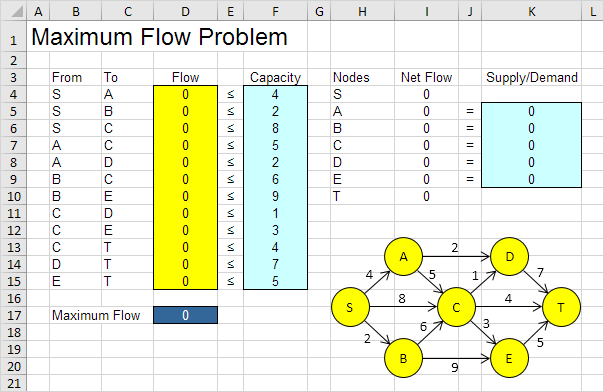
Le modèle que nous allons résoudre se présente comme suit dans Excel.
-
Pour formuler ce problème de débit maximal, répondez aux trois questions suivantes.
\une. Quelles sont les décisions à prendre? Pour ce problème, nous avons besoin d’Excel pour trouver le flux sur chaque arc. Par exemple, si le débit sur SB est 2, la cellule D5 est égal à 2.
\ B. Quelles sont les contraintes qui pèsent sur ces décisions? Le flux net (Flow Out – Débit In) du noeud A, B, C, D et E doivent être égales à 0. En d’autres termes, le flux Out = Débit In. En outre, chaque arc a une capacité fixe. Le débit de chaque arc doit être inférieure à cette capacité.
\ C. Quelle est la mesure globale de la performance de ces décisions? La mesure globale de la performance est le débit maximal, de sorte que l’objectif est de maximiser cette quantité. Le débit maximal est égal au débit du noeud S. Out
-
Pour rendre le modèle plus facile à comprendre, nommez les plages suivantes.
|
Range Name |
Cells |
|
From |
B4:B15 |
|
To |
C4:C15 |
|
Flow |
D4:D15 |
|
Capacity |
F4:F15 |
|
SupplyDemand |
K5:K9 |
|
MaximumFlow |
D17 |
-
Insérez les fonctions suivantes.
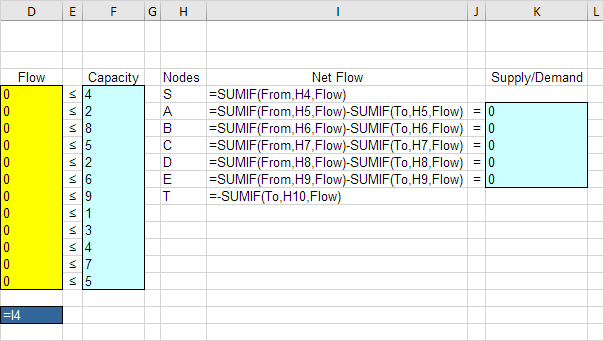
Explication: Le lien: exemples sumif / [SUMIF] fonctions calculer le flux net de chaque nœud. Pour le noeud A, la première fonction SOMME.SI résume les valeurs de la colonne de débit avec un « A » dans la colonne De (Flow Out). La deuxième fonction SOMME.SI résume les valeurs de la colonne de débit avec un « A » dans la colonne (Flow In). Débit maximal est égal à la valeur I4 cellulaire, ce qui est le flux de noeud S. Comme le nœud A, B, C, D et E ont un flux net de 0, réacheminés du noeud S sera égal débit dans de noeud T.
Trial and Error
Avec cette formulation, il devient facile d’analyser toute solution d’essai.
-
Par exemple, le chemin TDAA avec un flux de 2. Le chemin SCT avec un flux de 4. Le chemin SBET avec un flux de 2. Ces chemins d’écoulement total givea de 8
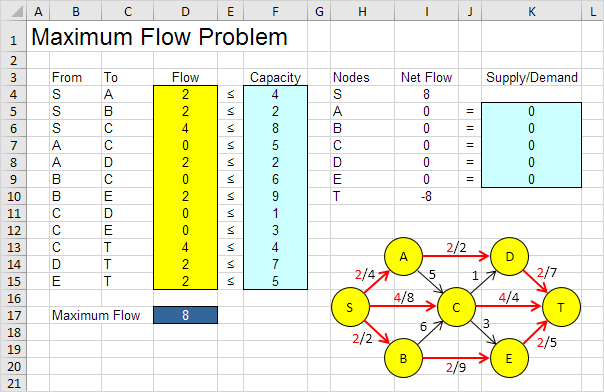
Il est pas nécessaire d’utiliser tâtonnement. Nous allons décrire ensuite comment Excel Solver peut être utilisé pour trouver rapidement la solution optimale.
Résoudre le modèle
Pour trouver la solution optimale, exécutez les étapes suivantes.
-
Dans l’onglet Données, dans le groupe Analyser, cliquez sur Solver.
Remarque: ne peut pas trouver le bouton Solver? Cliquez ici pour charger le complément Solver.
Entrez les paramètres du solveur (lire). Le résultat devrait être compatible avec l’image ci-dessous.
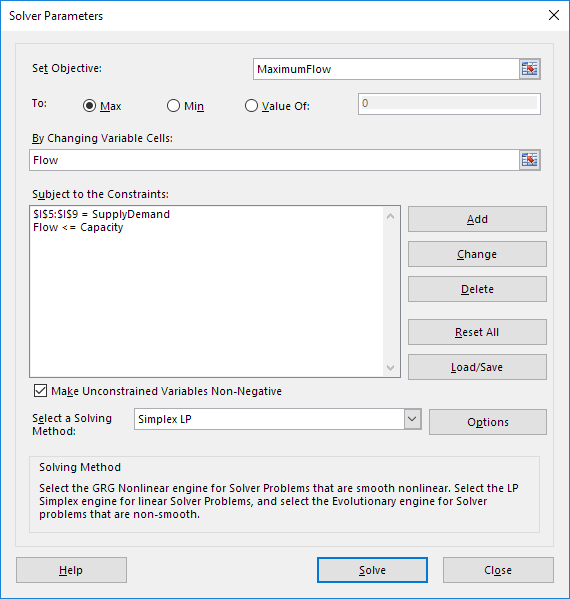
Vous avez le choix de taper les noms de plage ou en cliquant sur les cellules dans la feuille de calcul.
-
Entrez MaximumFlow pour l’objectif.
-
Cliquez sur Max.
-
Entrez flux pour le changement des cellules variables.
-
Cliquez sur Ajouter pour saisir la contrainte suivante.
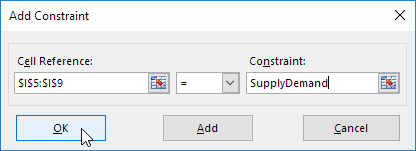
-
Cliquez sur Ajouter pour saisir la contrainte suivante.
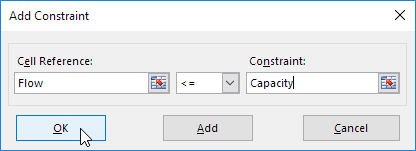
-
Cochez la case ‘Make Variables non sans contrainte négative’ et sélectionnez ‘Simplex LP’.
-
Enfin, cliquez sur Résoudre.
Résultat:
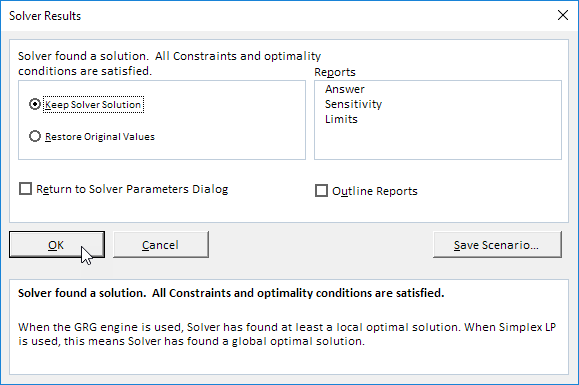
La solution optimale:
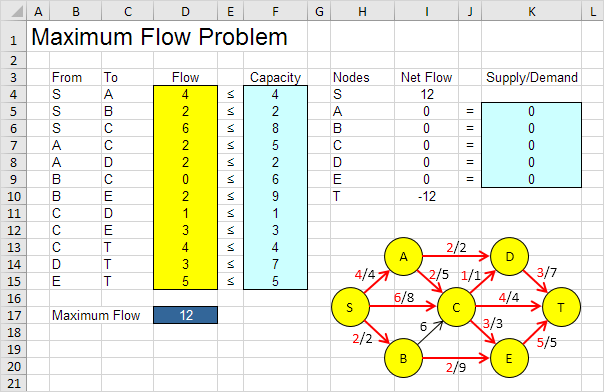
Conclusion: le chemin TDAA avec un flux de 2. Le chemin SCT avec un flux de 4. Le chemin SBET avec un flux de 2. Le chemin SCET avec un flux de 2. Le chemin Sacet avec un flux de 1. Le chemin SACDT avec un flux de 1. Ces chemins givea débit maximum de 12.