Comment faire l’analyse de régression Dans Excel
La régression est un outil d’analyse que nous utilisons pour analyser de grandes quantités de données et faire des prévisions et des prédictions dans Microsoft Excel.
Envie de prédire l’avenir? Non, nous n’allons pas apprendre l’astrologie. Nous sommes dans les nombres et nous allons apprendre l’analyse de régression dans Excel aujourd’hui.
Pour prédire les estimations futures, nous étudierons:
lien: # link1head [ANALYSE DE REGRESSION UTILISANT LES FONCTIONS EXCEL (RECHERCHE MANUELLE DE REGRESSION)] lien: # link2head [ANALYSE DE REGRESSION À L’AIDE D’UN OUTIL D’ANALYSE D’EXCEL ADD-IN]
* lien: # link3head [TABLEAU DE REGRESSION EN EXCEL]
Faisons-le …
Scénario:
Supposons que vous vendiez des boissons gazeuses. Ce sera cool si vous pouvez prédire:
-
Combien de boissons gazeuses seront vendues l’année prochaine selon les données de l’année précédente?
-
Quels domaines doivent être ciblés?
-
Et comment augmenter vos ventes en modifiant votre stratégie?
Ce sera génial et rentable. Pas vrai?… Je sais. Alors, commençons.
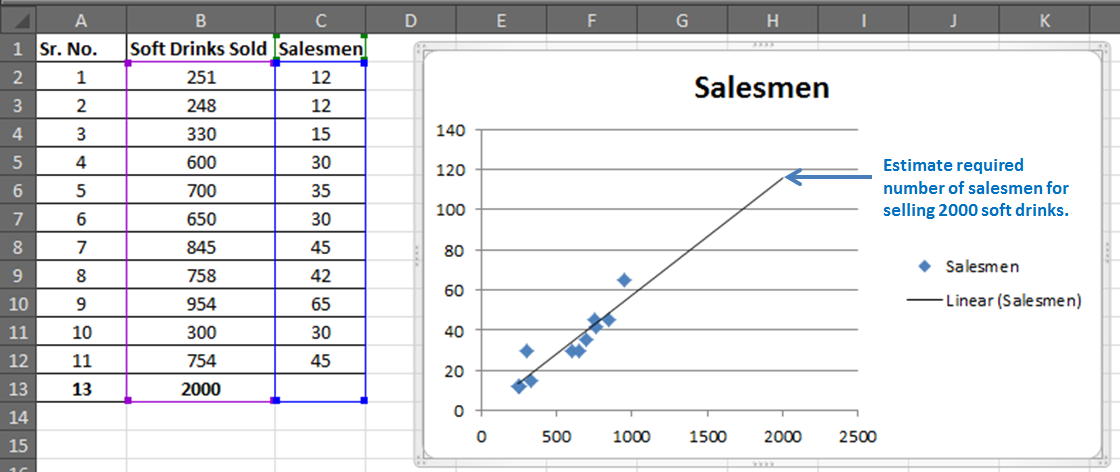
Vous avez 11 enregistrements de vendeurs et de boissons gazeuses vendus.
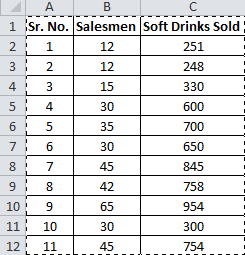
Maintenant, sur la base de ces données, vous voulez prédire le nombre de vendeurs nécessaires pour réaliser 2000 ventes de boissons gazeuses.

L’équation de régression est un outil pour faire des estimations aussi proches. Pour ce faire, nous devons d’abord connaître la régression.
ANALYSE DE REGRESSION À L’AIDE DES FONCTIONS EXCEL (RECHERCHE MANUELLE DE REGRESSION)
Cette partie vous permettra de mieux comprendre la régression que de simplement dire la procédure de régression Excel.
Introduction:
Régression linéaire simple:
L’étude de la relation entre deux variables est appelée régression linéaire simple. Où une variable dépend de l’autre variable indépendante. La variable dépendante est souvent appelée par des noms tels que Variable pilotée, réponse et cible. Et la variable indépendante est souvent prononcée comme une variable de conduite, de prédiction ou simplement indépendante.
Ces noms les décrivent clairement.
Maintenant, comparons cela à votre scénario. Vous souhaitez connaître le nombre de vendeurs nécessaires pour réaliser 2000 ventes. Donc ici, la variable dépendante est le nombre de vendeurs et la variable indépendante est les boissons gazeuses vendues.
La variable indépendante est principalement désignée par x et la variable dépendante par y. Dans notre cas, les boissons gazeuses sont vendues x et le nombre de vendeurs est y.
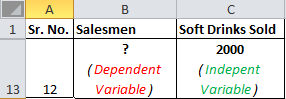
Si nous voulons savoir combien de boissons gazeuses seront vendues si nous nommons 200 vendeurs, alors le scénario sera vice-versa.
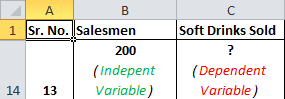
Passer à autre chose.
Les mathématiques «simples» de l’équation de régression linéaire:
Eh bien, ce n’est pas simple. Mais Excel a simplifié la tâche.
Nous devons prédire le nombre requis de vendeurs pour les 11 cas afin d’obtenir la 12e prédiction la plus proche.
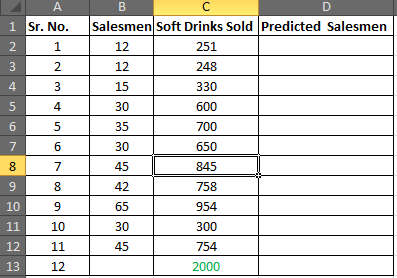
Disons:
La boisson gazeuse vendue est x
Le nombre de vendeurs est y
Le y prédit (nombre de vendeurs) également appelé équation de régression serait
|
* (relax, I’ve got it covered) |
Maintenant, vous devez vous demander où le stat vous obtiendrez la pente et l’interception. Ne vous inquiétez pas, Excel a des fonctions pour eux. Vous n’avez pas besoin d’apprendre à trouver la pente et à l’intercepter manuellement.
Si vous le souhaitez, je préparerai un tutoriel séparé pour cela. Faites-le moi savoir dans les commentaires. Ce sont des outils d’analyse de données importants.
Passons maintenant à notre calcul:
Étape 1: Préparez cette petite table

Étape 2: Trouvez la pente de la droite de régression
La fonction Excel pour les pentes est
|
=SLOPE(known_y’s,known_x’s) |
Vos known_y sont dans la plage B2: B12 et known_x’s sont dans la plage C2: C12
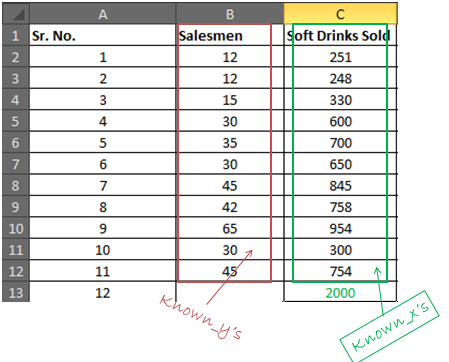
Dans la cellule B16, écrivez la formule ci-dessous
|
=SLOPE(B2:B12, C2:C12) |
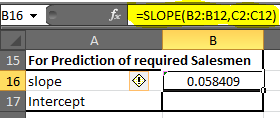
(_Remarque: la pente est également appelée coefficient de x dans l’équation de régression) _ Vous obtiendrez 0,058409. Arrondissez à 2 chiffres décimaux et vous obtiendrez 0,06.
Étape 3: Trouver l’interception de la ligne de régression
La fonction Excel pour l’interception est
|
=INTERCEPT(known_y’s, known_x’s)* |
Nous savons ce que sont nos x et y connus Dans la cellule B17, notez cette formule
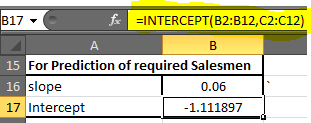
|
=INTERCEPT(B2:B12, C2:C12)* |
Vous obtiendrez une valeur de -1.1118969. Arrondissez à 2 chiffres décimaux. Vous obtiendrez -1,11. Notre équation de régression linéaire est = x0,06 + (-1,11). Maintenant, nous pouvons prédire facilement y en fonction de la cible x. Étape 4: * En D2, écrivez la formule ci-dessous
|
=C2*$B$16+$B$17 (Regression Equation) |
Vous obtiendrez une valeur de 13,55.
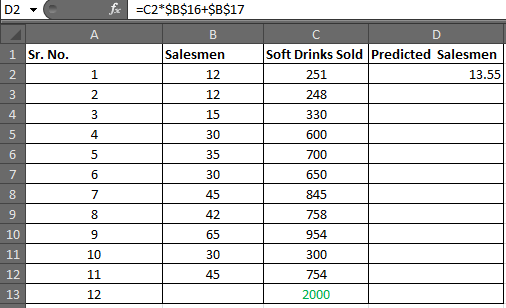
Sélectionnez D2 à D13 et appuyez sur CTRL + D pour remplir la formule dans la plage D2: D13
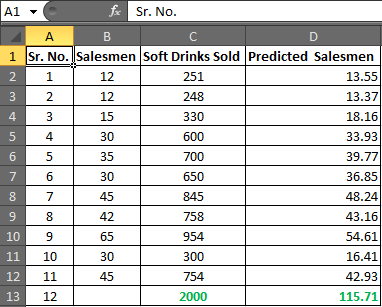
Dans la cellule D13, vous avez le nombre de vendeurs requis.
|
Hence, to achieve the target of 2000 Soft Drink Sales, you need an estimate of 115.71 salesmen or say 116 since it is illegal to cut humans into pieces. |
Maintenant, en utilisant cela, vous pouvez facilement effectuer une analyse hypothétique dans Excel. Changez simplement le nombre de ventes et cela vous montrera que de nombreux vendeurs seront nécessaires pour atteindre cet objectif de vente.
Jouez autour pour découvrir:
De combien d’effectifs avez-vous besoin pour augmenter vos ventes?
Combien de ventes augmenteront si vous augmentez vos vendeurs?
Rendez votre estimation plus fiable:
Vous savez maintenant que vous avez besoin de 116 vendeurs pour réaliser 2000 ventes.
En analytique, rien n’est dit et cru. Vous devez donner un pourcentage de fiabilité sur votre estimation. C’est comme donner un certificat de votre équation.