어떻게 Excel에서 Z.TEST 기능을 사용하는
이 기사에서는 Excel에서 Z.TEST 함수를 사용하는 방법을 배웁니다.
가설 검정이란 무엇이며 가설 검정을 위해 Z-Test를 사용하는 방법은 무엇입니까? 통계에서 가설 검정은 표본 데이터 세트라는 인구 데이터 세트의 일부를 기반으로 다른 분포 함수를 사용하여 모집단 데이터 세트의 평균 추정을 찾는 데 사용됩니다. 확인 데이터 분석이라고도하는 통계 가설은 일련의 무작위 변수를 통해 모델링 된 프로세스를 관찰하여 테스트 할 수있는 가설입니다. 가설에는 두 가지 유형이 있습니다. 하나는 주장 된 진술인 귀무 가설이고 다른 하나는 귀무 가설과 정반대 인 대체 가설입니다. 예를 들어, maggi 패킷에서 리드에 대한 최대 한계가 225ppm (백만 분율)을 초과하지 않아야한다고 말하고 누군가가 귀무 가설 (U ~ 0 ~으로 표시)과 대체 가설 (로 표시)보다 고정 한계 이상이라고 주장하는 경우 작성자 U ~ a ~)
U ~ 0 ~ = maggi 패킷의 리드 콘텐츠가 225ppm 이상입니다. U ~ a ~ = maggi 패킷의 납 함량이 225ppm 미만입니다.
따라서 위의 가설은 기본 상황이 분포 곡선의 오른쪽에 있기 때문에 오른쪽 꼬리 검정의 예입니다.
기본 상황이 왼쪽에 있으면 왼쪽 꼬리 테스트라고합니다. 단측 테스트를 설명하는 예를 하나 더 살펴 보겠습니다. 예를 들어 셀리나가 평균 60 번의 푸시 업을 할 수 있다고 말하면. 이제 그 진술을 의심하고 통계 용어로 상황을 가설하려고 할 수 있습니다. 그러면 null과 대립 가설이 아래에 나와 있습니다. U ~ 0 ~ = 셀리나는 60 개의 푸시 업을 할 수 있습니다 U ~ a ~ = 셀리나는 60 개의 푸시 업을 할 수 없습니다. 기본 상황이 주장 된 진술의 양쪽에있는 꼬리 테스트. 이러한 꼬리 검정은 통계의 결과에 영향을줍니다. 따라서 귀무 가설과 대립 가설을 신중하게 선택하십시오.
Z-검정 Z 검정은 귀무 가설 하의 검정 통계 분포를 정규 분포로 근사 할 수있는 통계 검정입니다. Z- 검정은 이미 모집단 분산을 알고있는 분포의 평균을 검정합니다. 중심 한계 정리로 인해 많은 검정 통계량은 큰 표본에 대해 대략적으로 정규 분포를 따릅니다. 테스트 통계는 정확한 z- 검정을 수행하기 위해 표준 편차와 같은 정규 분포를 알고 있어야한다고 가정합니다. 예를 들어, 투자자는 주식의 일일 평균 수익률이 1 %를 초과하는지 여부를 Z 테스트를 사용하여 평가할 수 있는지 테스트하려고합니다. Z- 통계 또는 Z- 점수 *는 Z- 검정에서 도출 된 점수가 평균 모집단보다 높거나 낮은 표준 편차 수를 나타내는 숫자입니다. 수학적으로 먼저 귀무 가설을 결정하고 공식을 사용하여 분포에 대한 Z 점수를 계산합니다.
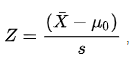
여기서 X (막대 포함)는 표본 배열의 평균입니다. U ~ 0 ~ 추정 모집단 평균 s는 s가 std / (n) ^ 1 / 2 ^ (n은 표본 크기)와 같은 표준 편차입니다. .
위에서 언급했듯이 Z-테스트는 표준 정규 분포를 따릅니다. 따라서 Excel에서 수학적으로 다음 공식을 따릅니다.
Z.TEST (array, x, sigma) = 1- Norm.S.Dist ((Average (array)-x) / (sigma / (n) ^ 1 / 2 ^), TRUE)
또는 시그마가 생략 된 경우 :
Z.TEST (array, x) = 1- Norm.S.Dist ((Average (array)-x) / (STDEV (array) / (n) ^ 1 / 2 ^), TRUE)
여기서 x는 표본 평균 AVERAGE (배열)이고 n은 COUNT (배열)입니다.
주어진 두 데이터 세트 (실제 및 관찰) 간의 관계를 계산하기 위해 Z.TEST 함수를 사용하여 Z 테스트를 수행하는 방법을 알아 보겠습니다.
Excel의 Z.TEST 함수
Z.TEST 함수는 표본 평균이 데이터 세트 (배열)의 관측치 평균보다 클 확률을 반환합니다. 이 함수는 다음 인수를 사용합니다.
Z.TEST 단측 확률에 대한 함수 구문 :
|
=Z.TEST ( array , x , [sigma] ) |
이 함수는 양측 확률을 통근하는데도 사용할 수 있습니다.
Z.TEST 단측 확률에 대한 함수 구문 :
|
=2 * MIN(Z.TEST ( array , x , [sigma] ), 1-Z.TEST ( array , x , [sigma] ) ) |
array : 표본 데이터 분포 x : z 검정이 평가되는 값 [sigma] * : [선택 사항] 모집단 (알려진) 표준 편차. 생략하면 표본 표준 편차가 사용됩니다.
예 :
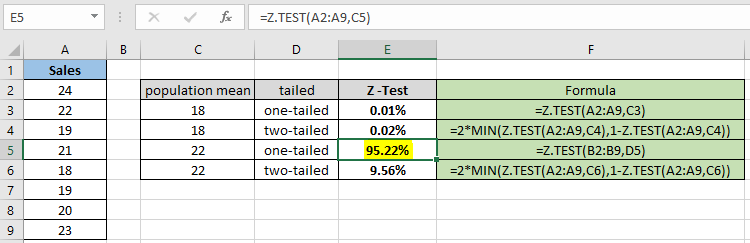
이 모든 것들은 이해하기 어려울 수 있습니다. 예제를 사용하여 함수를 사용하는 방법을 이해합시다. 여기에 샘플 데이터 세트 Sales가 있으며 단측 검정을 가정하고 주어진 가설 모집단 평균에 대한 Z 검정 확률을 찾아야합니다.
공식 사용 :
|
= Z.TEST( A2:A9 , C3 ) |
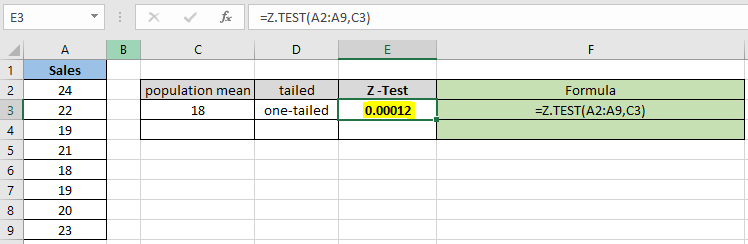
확률 값은 십진수로 표시되므로 값을 백분율로 변환하여 셀 형식을 백분율로 변경할 수 있습니다.
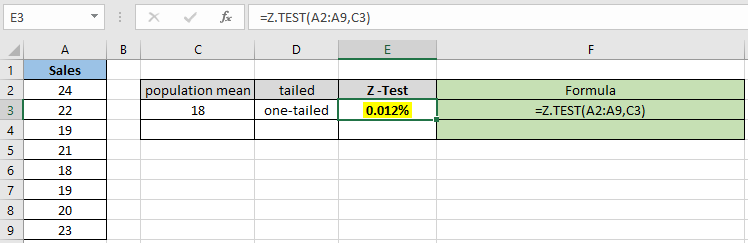
보시다시피 가정 된 모집단 평균 18의 확률 값은 단측 분포에 대해 0.012 %가됩니다. 이제 동일한 모수를 갖는 두 꼬리 분포를 가정 할 확률을 계산합니다.
공식 사용 :
|
= 2 * MIN( Z.TEST(A2:A9,C4) , 1 – Z.TEST(A2:A9,C4) ) |
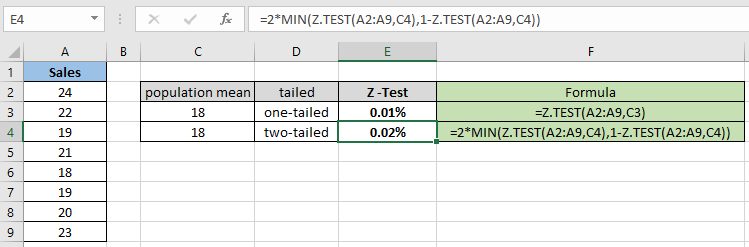
양측 분포의 경우 동일한 샘플 데이터 세트에 대해 확률이 두 배가됩니다. 따라서 귀무 가설과 대립 가설을 확인하는 것이 필요합니다. 이제 다양한 가설 모집단 평균과 단측 분포에 대한 확률을 계산합니다.
공식 사용 :
|
= Z.TEST( A2:A9 , C5 ) |
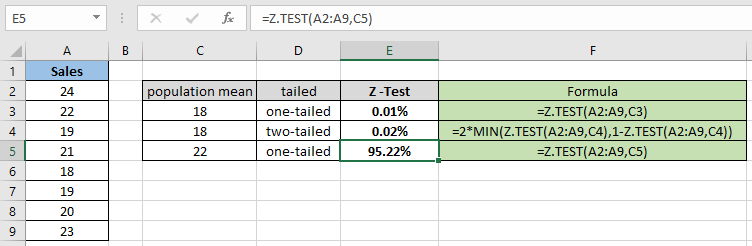
보시다시피, 가정 된 모집단 평균 22의 확률 값은 단측 분포에 대해 95.22 %로 나옵니다. 이제 동일한 모수를 갖는 두 꼬리 분포를 가정 할 확률을 계산합니다.
공식 사용 :
|
= 2 * MIN( Z.TEST(A2:A9,C6) , 1 – Z.TEST(A2:A9,C6) ) |
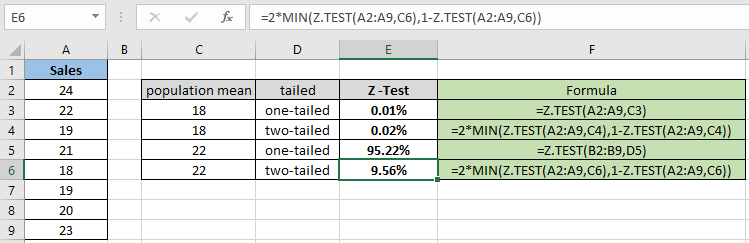
위의 스냅 샷과 다를 수 있으므로 양측 분포를 계산할 때 확률 값이 줄어 듭니다. 이 함수는 가정 된 모집단 평균 22에 대해 9.56 %를 반환합니다.
Z.TEST는 기본 모집단 평균이 0 일 때 표본 평균이 관측 된 값 AVERAGE (배열)보다 클 확률을 나타냅니다. 정규 분포의 대칭에서 AVERAGE (배열) <x이면 Z.TEST가 0.5보다 큰 값을 반환합니다.
다음은 Excel에서 Z.TEST 함수를 사용한 모든 관찰 메모입니다
참고 :
-
이 기능은 숫자로만 작동합니다. 모집단 평균 또는 시그마 인수가 숫자가 아니면 함수는 #VALUE! 오류.
-
십진수 값 또는 백분율 값은 Excel에서 동일한 값입니다.
필요한 경우 값을 백분율로 변환하십시오.
-
이 함수는 #NUM! 시그마 인수가 0 인 경우 오류입니다.
-
이 함수는 # N / A!를 반환합니다. 제공된 배열이 비어 있으면 오류가 발생합니다.
-
이 함수는 # DIV / 0!을 반환합니다. 오류, .. 배열의 표준 편차가 0이고 시그마 인수가 생략 된 경우.
-
배열에 하나의 값만 포함 된 경우.
-
Excel에서 Z.TEST 함수를 사용하는 방법에 대한이 기사가 설명이되기를 바랍니다. 여기에서 통계 공식 및 관련 Excel 함수에 대한 더 많은 기사를 찾아보십시오. 블로그가 마음에 들면 Facebook에서 친구들과 공유하세요. 또한 Twitter와 Facebook에서 우리를 팔로우 할 수 있습니다. 우리는 여러분의 의견을 듣고 싶습니다. 우리가 작업을 개선, 보완 또는 혁신하고 여러분을 위해 개선 할 수있는 방법을 알려주십시오. [email protected]로 이메일을 보내주십시오.
관련 기사 :
link : / statistical-formulas-how-to-use-t-test-function-in-excel [Excel에서 Excel TEST 기능 사용 방법]: T.TEST는 분석의 신뢰도를 판단하는 데 사용됩니다. 수학적으로 두 샘플의 평균이 같은지 여부를 아는 데 사용됩니다. T.TEST는 귀무 가설을 수락하거나 거부하는 데 사용됩니다.
link : / statistical-formulas-how-to-use-excel-f-test-function [Excel에서 Excel F.TEST 함수 사용 방법]: F.TEST 함수는 두 샘플의 F 통계를 계산하는 데 사용됩니다. 내부적으로 탁월하고 Null Hypothesis에서 F 통계의 양측 확률을 반환합니다.
link : / statistical-formulas-how-to-use-the-devsq-function-in-excel [Excel에서 DEVSQ 함수 사용 방법]: DEVSQ 함수는 제곱합을 계산하는 내장 통계 함수입니다. 제공된 데이터 값 범위의 평균 또는 평균으로부터의 편차.
link : / statistical-formulas-how-to-use-excel-normdist-function [Excel NORM.DIST 함수 사용 방법]: NORMDIST 함수를 사용하여 미리 지정된 값에 대한 정규 누적 분포에 대한 Z 점수를 계산합니다. 뛰어나다.
link : / statistical-formulas-how-to-use-excel-norm-inv-function [Excel NORM.INV 함수 사용 방법]: 미리 지정된 확률에 대한 정규 누적 분포에 대한 Z 점수의 역 계산 Excel에서 NORM.INV 함수를 사용하여 값.
link : / excel-financial-formulas-how-to-calculate-standard-deviation-in-excel [Excel에서 표준 편차를 계산하는 방법]: * 표준 편차를 계산하기 위해 Excel에는 다양한 기능이 있습니다. 표준 편차는 분산 값의 제곱근이지만 분산보다 데이터 세트에 대해 더 많이 알려줍니다.
link : / statistical-formulas-excel-var-function [Excel에서 VAR 함수 사용 방법]: Excel에서 VAR 함수를 사용하여 Excel에서 샘플 데이터 세트의 분산을 계산합니다.
인기 기사 :
link : / tips-if-condition-in-excel [Excel에서 IF 함수 사용 방법]: Excel의 IF 문은 조건을 확인하고 조건이 TRUE 인 경우 특정 값을 반환하거나 FALSE 인 경우 다른 특정 값을 반환합니다. .
link : / formulas-and-functions-introduction-of-vlookup-function [Excel에서 VLOOKUP 함수 사용 방법]: 다양한 범위의 값을 조회하는 데 사용되는 Excel에서 가장 많이 사용되는 인기 함수 중 하나입니다. 및 시트. link : / excel-formula-and-function-excel-sumif-function [Excel에서 SUMIF 함수 사용 방법]: 대시 보드의 또 다른 필수 기능입니다. 이를 통해 특정 조건에 대한 값을 합산 할 수 있습니다.
link : / tips-countif-in-microsoft-excel [Excel에서 COUNTIF 함수 사용 방법]:이 놀라운 함수를 사용하여 조건으로 값을 계산합니다. 특정 값을 계산하기 위해 데이터를 필터링 할 필요가 없습니다. Countif 기능은 대시 보드를 준비하는 데 필수적입니다.