Wie Regressionsanalyse in Excel tun
Regression ist ein Analysetool, mit dem wir große Datenmengen analysieren und Prognosen und Vorhersagen in Microsoft Excel erstellen.
Möchten Sie die Zukunft vorhersagen? Nein, wir werden keine Astrologie lernen. Wir stehen auf Zahlen und werden heute die Regressionsanalyse in Excel lernen.
Um zukünftige Schätzungen vorherzusagen, werden wir Folgendes untersuchen:
link: # link1head [REGRESSIONSANALYSE MIT EXCEL-FUNKTIONEN (MANUELLE REGRESSIONSFINDUNG)] link: # link2head [REGRESSIONSANALYSE MIT EXCEL-ANALYSE-TOOLPAK HINZUFÜGEN]
* link: # link3head [REGRESSIONSTABELLE IN EXCEL]
Lass es uns tun …
Szenario:
Nehmen wir an, Sie verkaufen alkoholfreie Getränke. Wie cool wird es sein, wenn Sie vorhersagen können:
-
Wie viele alkoholfreie Getränke werden im nächsten Jahr nach Angaben des Vorjahres verkauft?
-
Welche Bereiche müssen fokussiert werden?
-
Und wie können Sie Ihren Umsatz steigern, indem Sie Ihre Strategie ändern?
Es wird gewinnbringend großartig sein. Richtig? … ich weiß. Also lasst uns anfangen.
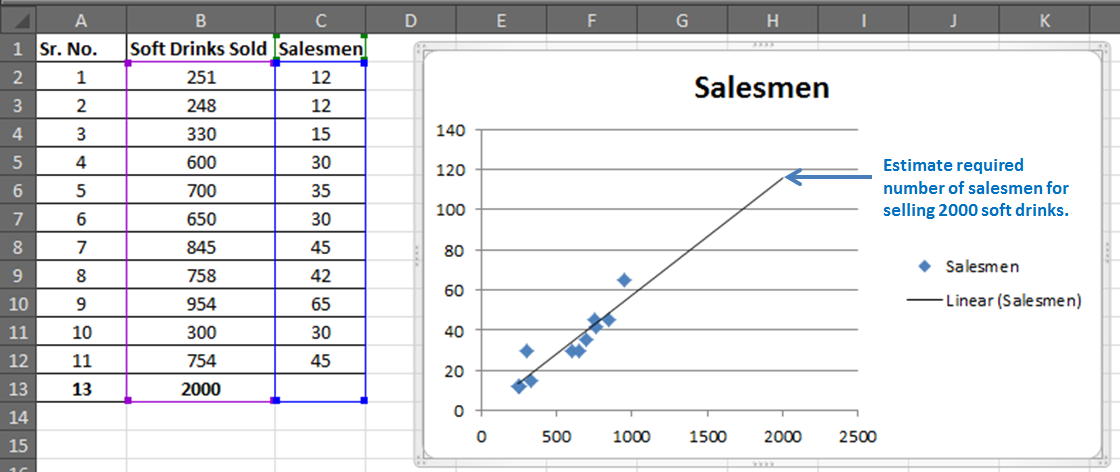
Sie haben 11 Aufzeichnungen von Verkäufern und verkauften alkoholfreien Getränken.
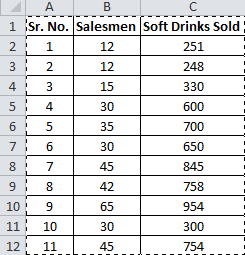
Basierend auf diesen Daten möchten Sie nun die Anzahl der Verkäufer vorhersagen, die erforderlich sind, um 2000 Verkäufe von Erfrischungsgetränken zu erzielen.

Die Regressionsgleichung ist ein Werkzeug, um solche genauen Schätzungen vorzunehmen. Dazu müssen wir zuerst die Regression kennen.
REGRESSIONSANALYSE MIT EXCEL-FUNKTIONEN (MANUELLE REGRESSIONSFINDUNG)
In diesem Teil werden Sie die Regression besser verstehen, als nur das Excel-Regressionsverfahren zu erklären.
Einführung:
Einfache lineare Regression:
Die Untersuchung der Beziehung zwischen zwei Variablen wird als einfache lineare Regression bezeichnet. Wobei eine Variable von der anderen unabhängigen Variablen abhängt. Die abhängige Variable wird häufig mit Namen wie Driven, Response und Target Variable aufgerufen. Und die unabhängige Variable wird oft als Fahr-, Prädiktor- oder einfach als unabhängige Variable ausgesprochen.
Diese Namen beschreiben sie klar.
Vergleichen wir dies nun mit Ihrem Szenario. Sie möchten wissen, wie viele Verkäufer erforderlich sind, um 2000 Verkäufe zu erzielen. Die abhängige Variable ist hier also die Anzahl der Verkäufer und die unabhängige Variable verkauft alkoholfreie Getränke.
Die unabhängige Variable wird meist als x und die abhängige Variable als y bezeichnet. In unserem Fall werden alkoholfreie Getränke x verkauft und die Anzahl der Verkäufer beträgt y.
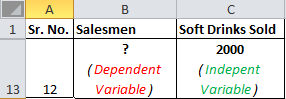
Wenn wir wissen wollen, wie viele alkoholfreie Getränke verkauft werden, wenn wir 200 Verkäufer ernennen, ist das Szenario umgekehrt.
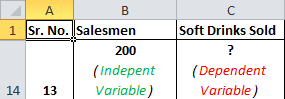
Weitermachen.
Die „einfache“ Mathematik der linearen Regressionsgleichung:
Nun, es ist nicht einfach. Aber Excel hat es einfach gemacht.
Wir müssen die erforderliche Anzahl von Verkäufern für alle 11 Fälle vorhersagen, um die zwölftnächste Vorhersage zu erhalten.
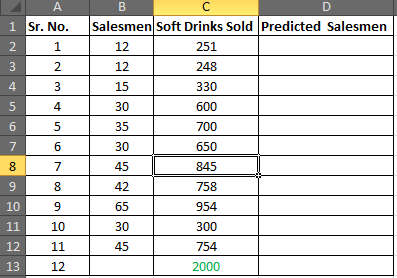
Sagen wir:
Soft Drink Verkauft ist x
Die Anzahl der Verkäufer beträgt y
Das vorhergesagte y (Anzahl der Verkäufer), auch Regressionsgleichung genannt, wäre
|
* (relax, I’ve got it covered) |
Jetzt müssen Sie sich fragen, wo die Stat Sie die Steigung und Abfangen bekommen wird. Keine Sorge, Excel hat Funktionen für sie. Sie müssen nicht lernen, wie Sie die Steigung finden und manuell abfangen.
Wenn Sie möchten, werde ich dafür ein separates Tutorial vorbereiten. Lass es mich in den Kommentaren wissen. Dies sind einige wichtige Datenanalysetools.
Kommen wir nun zu unserer Berechnung:
Schritt 1: Bereiten Sie diese kleine Tabelle vor

Schritt 2: Finden Sie die Steigung der Regressionslinie
Die Excel-Funktion für Steigungen ist
|
=SLOPE(known_y’s,known_x’s) |
Ihre bekannten_y befinden sich im Bereich B2: B12 und bekannte_x befinden sich im Bereich C2: C12
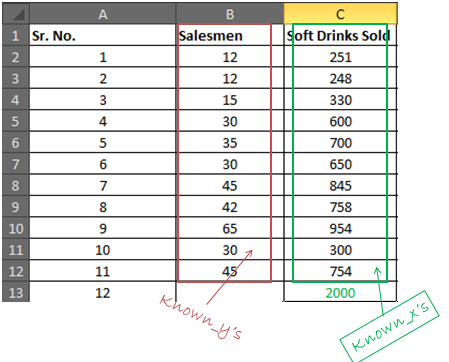
Schreiben Sie in Zelle B16 die folgende Formel
|
=SLOPE(B2:B12, C2:C12) |
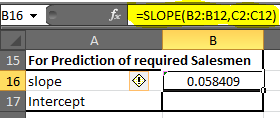
(_Hinweis: Die Steigung wird in der Regressionsgleichung auch als Koeffizient von x bezeichnet.) _ Sie erhalten 0,058409. Runden Sie auf 2 Dezimalstellen auf und Sie erhalten 0,06.
Schritt 3: Finden Sie den Achsenabschnitt der Regressionslinie
Die Excel-Funktion für den Achsenabschnitt ist
|
=INTERCEPT(known_y’s, known_x’s)* |
Wir wissen, was unsere bekannten x und y sind. Schreiben Sie in Zelle B17 diese Formel auf
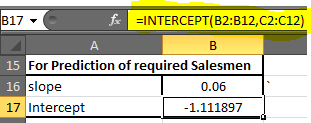
|
=INTERCEPT(B2:B12, C2:C12)* |
Sie erhalten einen Wert von -1,1118969. Auf 2 Dezimalstellen aufrunden. Sie erhalten -1,11. Unsere lineare Regressionsgleichung ist = x0,06 + (-1,11). Jetzt können wir das mögliche y in Abhängigkeit vom Ziel x leicht vorhersagen. Schritt 4: * Schreiben Sie in D2 die folgende Formel
|
=C2*$B$16+$B$17 (Regression Equation) |
Sie erhalten einen Wert von 13,55.
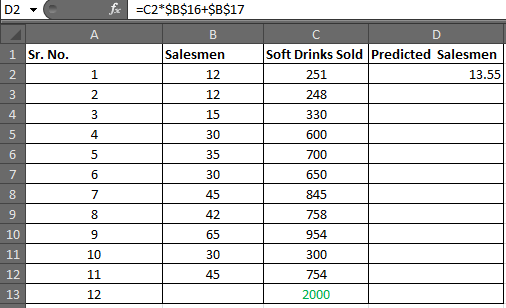
Wählen Sie D2 bis D13 und drücken Sie STRG + D, um die Formel im Bereich D2: D13
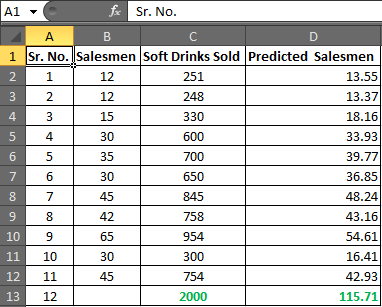
auszufüllen In Zelle D13 haben Sie die erforderliche Anzahl von Verkäufern.
|
Hence, to achieve the target of 2000 Soft Drink Sales, you need an estimate of 115.71 salesmen or say 116 since it is illegal to cut humans into pieces. |
Mit dieser Funktion können Sie jetzt problemlos eine Was-wäre-wenn-Analyse in Excel durchführen. Ändern Sie einfach die Anzahl der Verkäufe und es werden Ihnen viele Verkäufer angezeigt, die erforderlich sind, um dieses Verkaufsziel zu erreichen.
Spielen Sie herum, um herauszufinden:
Wie viel Personal benötigen Sie, um den Umsatz zu steigern?
Wie viele Verkäufe werden steigen, wenn Sie Ihre Verkäufer erhöhen?
Machen Sie Ihre Schätzung zuverlässiger:
Jetzt wissen Sie, dass Sie 116 Verkäufer benötigen, um 2000 Verkäufe zu tätigen.
In der Analytik wird nichts nur gesagt und geglaubt. Sie müssen einen Prozentsatz der Zuverlässigkeit Ihrer Schätzung angeben. Es ist wie ein Zertifikat Ihrer Gleichung zu geben.