Come utilizzare la funzione COMP.RADQ in Excel
In questo articolo, impareremo come utilizzare la funzione IMSQRT in Excel. Numero COMPLESSO (inumber) in Excel derivato per numero matematico avente coefficienti reali e immaginari. In matematica lo chiamiamo coefficiente di io j * (iota).
i = √-1 La radice quadrata di un numero negativo non è possibile, quindi ai fini del calcolo, √-1 è chiamato immaginario e lo chiama iota (i o j) *. Per il calcolo di alcuni termini come mostrato di seguito.
2 + √-25 = 2 + √-125 = 2 + √-1√25 = 2 + √-1 5 = 2 + 5i Questa equazione qui è un numero complesso (in numero) con 2 parti diverse chiamate parte reale e immaginaria parte Il coefficiente di iota (i) che è 5 è chiamato come parte immaginaria e l’altra parte 2 * è chiamata la parte reale del numero complesso.
Il numero complesso (inumber) è scritto nel formato X iY.
La radice quadrata complessa di un numero complesso (X + iY) è data dalla radice quadrata di (X iY) = √r Cos (/ 2) + i √r Sin (/ 2)
Qui . X e Y sono i coefficienti della parte reale e immaginaria del numero complesso (in numero). . r è uguale alla somma del quadrato della parte reale e immaginaria. r = √X ^ 2 ^ + Y ^ 2 ^. Cos e Sin sono i caratteri trigonometrici dove è uguale alla tangente inversa di (Y / X)
tan ^ -1 ^ (Y / X)
La funzione IMSQRT restituisce la radice quadrata complessa del numero complesso (inumber) avente sia la parte reale che quella immaginaria.
Sintassi:
=IMSQRT (inumber)
inumber: numero complesso avente sia reale che immaginario Comprendiamo questa funzione usandola in un esempio.
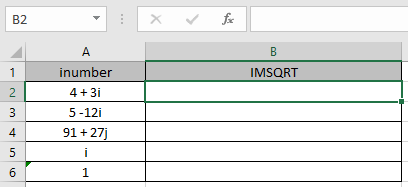
Qui abbiamo valori per i quali dobbiamo ottenere la radice quadrata complessa del numero complesso di input (inumber)
Usa la formula:
=IMSQRT (A2)
A2: numero complesso (inumber) fornito come riferimento di cella.
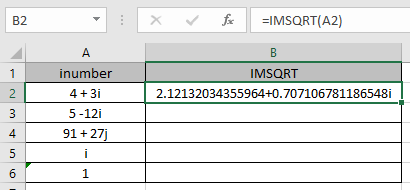
Come puoi vedere il numero complesso che ha real_num = 4 e parte immaginaria = 3. La formula restituisce la radice quadrata complessa del numero complesso.
Il segno del coefficiente di i (iota) viene modificato. Ora copia la formula nelle altre celle rimanenti usando il tasto di scelta rapida Ctrl + D *.
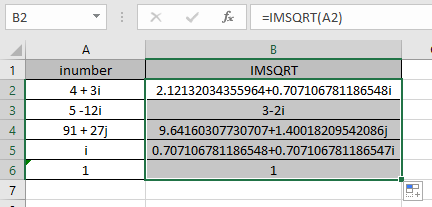
Come puoi vedere la formula della funzione IMSQRT fornisce risultati ottimali.
La tabella mostra qui spiega di più sui risultati
|
inumber |
Real part (X) |
Imaginary part (Y) |
IMSQRT |
|
i = 0 + 1i |
0 |
1 |
0.70 + 0.70 i |
|
1 = 1 + 0i |
1 |
0 |
1 |
Nota : . La formula restituisce #NUM! errore se il numero complesso non ha i minuscoli o j * (iota).
-
La formula restituisce il #VALORE! Errore se il numero complesso non ha il formato del numero complesso corretto.
Spero che tu abbia capito come utilizzare la funzione IMSQRT e la cella di riferimento in Excel. Esplora altri articoli sulle funzioni matematiche di Excel qui.
Non esitare a esprimere la tua domanda o il tuo feedback per l’articolo precedente.
Articoli correlati
link: / funzioni-matematiche-excel-log10-funzione [Come usare la funzione LOG10 di Excel]
link: / excel-formula-and-function-how-to-use-the-imexp-function-in-excel [Come usare la funzione IMEXP in Excel]
link: / excel-formula-and-function-how-to-use-the-imconjugate-function-in-excel [Come usare la funzione IMCONJUGATE in Excel]
link: / funzioni-matematiche-come-usare-la-funzione-argomento-in-excel [Come usare la funzione IMARGUMENT in Excel]
Articoli popolari
link: / excel-generals-how-to-edit-a-dropdown-list-in-microsoft-excel [Edit a dropdown list]
link: / tips-conditional-formatting-with-if-statement [If with conditional formatting]
link: / logical-formas-if-function-with-wildcards [If with wildcards]
link: / lookup-formas-vlookup-by-date-in-excel [Vlookup per data]