Регрессия — это инструмент анализа, который мы используем для анализа больших объемов данных и создания прогнозов и предсказаний в Microsoft Excel.

regression analysis excel

Хотите предсказать будущее? Нет, мы не собираемся изучать астрологию. Мы занимаемся числами, и сегодня мы изучим регрессионный анализ в Excel.

Чтобы предсказать будущие оценки, мы будем изучать:

link: # link1head [АНАЛИЗ РЕГРЕССИИ С ИСПОЛЬЗОВАНИЕМ ФУНКЦИЙ EXCEL (РУЧНОЙ ПОИСК РЕГРЕССИИ)] ссылка: # link2head [АНАЛИЗ РЕГРЕССИИ С ИСПОЛЬЗОВАНИЕМ ДОПОЛНИТЕЛЬНОГО ПАКЕТА EXCEL ANALYSIS TOOLPAK]

* ссылка: # link3head [ДИАГРАММА РЕГРЕССИИ В EXCEL]

Давай сделаем это …​

Сценарий:

Предположим, вы продаете безалкогольные напитки. Как будет круто, если ты сможешь предсказать:

  • Сколько безалкогольных напитков будет продано в следующем году по данным предыдущего года?

  • На какие поля нужно обратить внимание?

  • И как можно увеличить продажи, изменив свою стратегию?

Будет круто выгодно. Верно?… Я знаю. Итак, приступим.

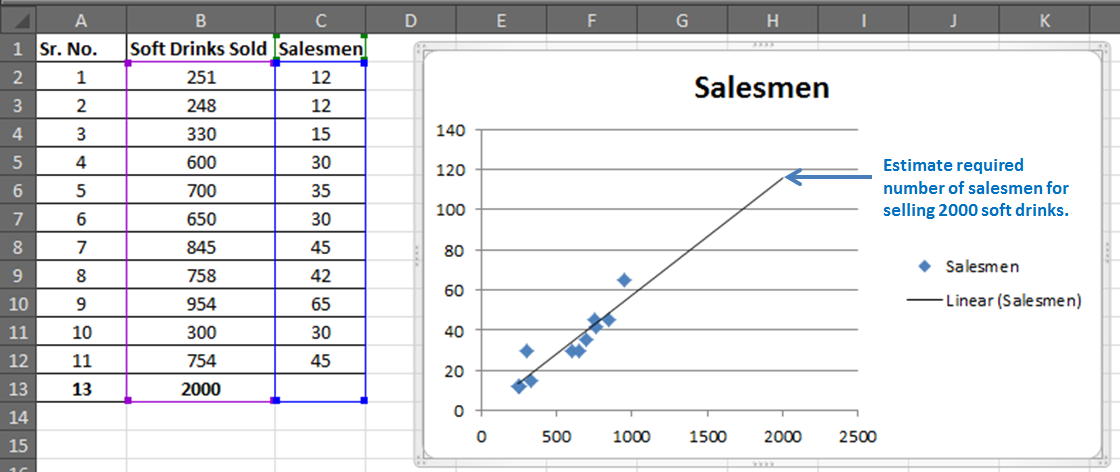
У вас есть 11 записей о продавцах и проданных безалкогольных напитках.

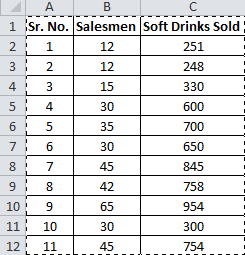
regression analysis excel

Теперь на основе этих данных вы хотите спрогнозировать количество продавцов, необходимое для достижения 2000 продаж безалкогольных напитков.

regression analysis in excel

Уравнение регрессии — инструмент для таких точных оценок. Для этого нам сначала нужно знать регрессию.

АНАЛИЗ РЕГРЕССИИ С ПОМОЩЬЮ ФУНКЦИЙ EXCEL (РУЧНОЙ ПОИСК РЕГРЕССИИ)

Эта часть поможет вам лучше понять регрессию, чем просто описание процедуры регрессии в Excel.

Введение:

Простая линейная регрессия:

Изучение взаимосвязи между двумя переменными называется простой линейной регрессией. Где одна переменная зависит от другой независимой переменной. Зависимая переменная часто вызывается такими именами, как Driven, Response и Target variable. А независимая переменная часто произносится как управляющая, предикторная или просто независимая переменная.

Эти имена ясно описывают их.

kcKoLq4gi

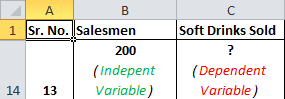
А теперь сравним это с вашим сценарием. Вы хотите знать количество продавцов, необходимое для достижения 2000 продаж. Итак, здесь зависимая переменная — это количество продавцов, а независимая переменная — это продажи безалкогольных напитков.

Независимая переменная обычно обозначается как x, а зависимая переменная как y. В нашем случае безалкогольных напитков продается x, а количество продавцов — y.

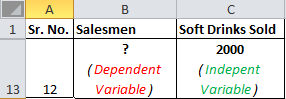
unnamed (11)

Если мы хотим знать, сколько безалкогольных напитков будет продано, если мы назначим 200 продавцов, то сценарий будет обратным.

unnamed (12)

Двигаемся дальше.

«Простая» математика уравнения линейной регрессии:

Что ж, это не просто. Но Excel сделал это просто.

Нам нужно спрогнозировать необходимое количество продавцов для всех 11 случаев, чтобы получить 12-й ближайший прогноз.

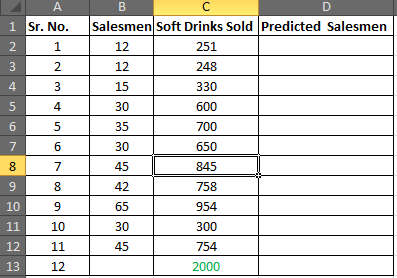
pasted image 0 (39)

Скажем:

Продано безалкогольных напитков x

Количество Продавцов y

Прогнозируемое y (количество продавцов), также называемое уравнением регрессии, будет

x`Slope+`Intercept

* (relax, I’ve got it covered)

Теперь вам должно быть интересно, где stat вы получите наклон и точку пересечения. Не волнуйтесь, в Excel есть функции для них. Не нужно учиться находить уклон и перехватывать его вручную.

Если хотите, я подготовлю для этого отдельный урок. Дайте мне знать в разделе комментариев. Это некоторые важные инструменты анализа данных.

Теперь перейдем к нашим расчетам:

Шаг 1: Подготовьте эту маленькую таблицу

pasted image 0 (40)

Шаг 2: Найдите наклон линии регрессии

Функция Excel для уклонов:

=SLOPE(known_y’s,known_x’s)

Ваши известные_y находятся в диапазоне B2: B12, а известные_x находятся в диапазоне C2: C12

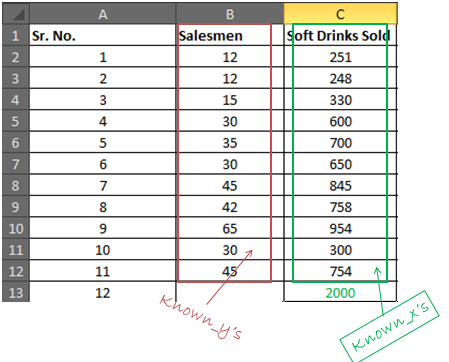
pasted image 0 (41)

В ячейке B16 запишите формулу ниже

=SLOPE(B2:B12, C2:C12)

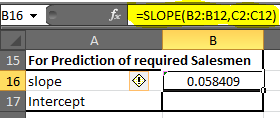
pasted image 0 (42)

(_Примечание: наклон также называется коэффициентом x в уравнении регрессии) _ Вы получите 0,058409. Округлите до 2 десятичных цифр, и вы получите 0,06.

Шаг 3: Найдите точку пересечения линии регрессии

Функция Excel для точки пересечения:

=INTERCEPT(known_y’s, known_x’s)*

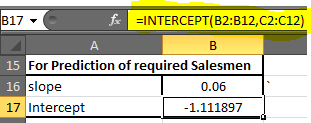
Мы знаем, каковы наши известные значения x и y. В ячейке B17 запишите эту формулу

pasted image 0 (43)

=INTERCEPT(B2:B12, C2:C12)*

Вы получите значение -1,1118969. Округление до 2 десятичных цифр. Вы получите -1.11. Наше уравнение линейной регрессии: = x0,06 + (-1,11). Теперь мы можем легко предсказать возможное y в зависимости от целевого x. Шаг 4: * В D2 напишите формулу ниже

=C2*$B$16+$B$17 (Regression Equation)

Вы получите значение 13,55.

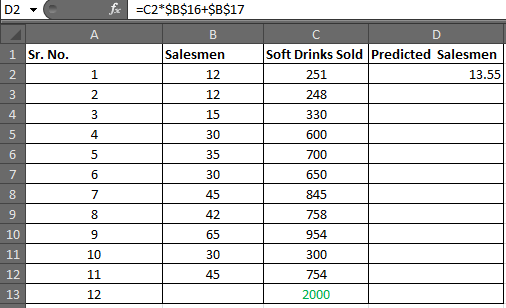
pasted image 0 (44)

Выберите от D2 до D13 и нажмите CTRL + D, чтобы заполнить формулу в диапазоне D2: D13

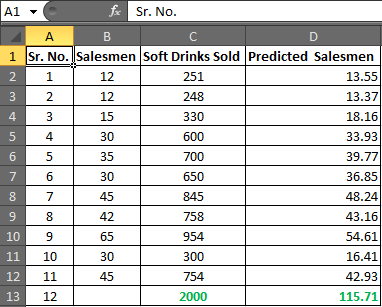
pasted image 0 (45)

В ячейке D13 указано необходимое количество продавцов.

Hence, to achieve the target of 2000 Soft Drink Sales, you need

an estimate of 115.71 salesmen or say 116 since it is illegal to cut

humans into pieces.

Теперь, используя это, вы можете легко провести анализ «что-если» в Excel. Просто измените количество продаж, и вы увидите, сколько продавцов потребуется для достижения этой цели.

Поэкспериментируйте, чтобы узнать:

Сколько сотрудников вам нужно для увеличения продаж?

На сколько продаж вырастет, если вы увеличите количество продавцов?

Сделайте свою оценку более надежной:

Теперь вы знаете, что вам нужно 116 продавцов, чтобы совершить 2000 продаж.

В аналитике ничего не говорят и не верят. Вы должны указать процент надежности своей оценки. Это все равно, что дать свидетельство о вашем уравнении.