回帰分析でExcelを実行する方法
回帰は分析ツールであり、Microsoft Excelで大量のデータを分析し、予測と予測を行うために使用します。
未来を予測したいですか?いいえ、占星術を学ぶつもりはありません。私たちは数字に興味があり、今日はExcelで回帰分析を学びます。
将来の見積もりを予測するために、次のことを検討します。
link:#link1head [Excel関数を使用した回帰分析(手動回帰検出)] link:#link2head [Excelの分析ツールパックアドインを使用した回帰分析]
* link:#link3head [Excelの回帰チャート]
やってみましょう…
シナリオ:
ソフトドリンクを販売しているとしましょう。あなたが予測できるなら、それはどれほどクールでしょう:
-
昨年のデータに基づいて、来年は何個の清涼飲料が販売されますか?
-
どの分野に焦点を当てる必要がありますか?
-
そして、戦略を変えることでどのように売上を増やすことができますか?
それは有益に素晴らしいでしょう。そうですか…わかっています。それでは始めましょう。
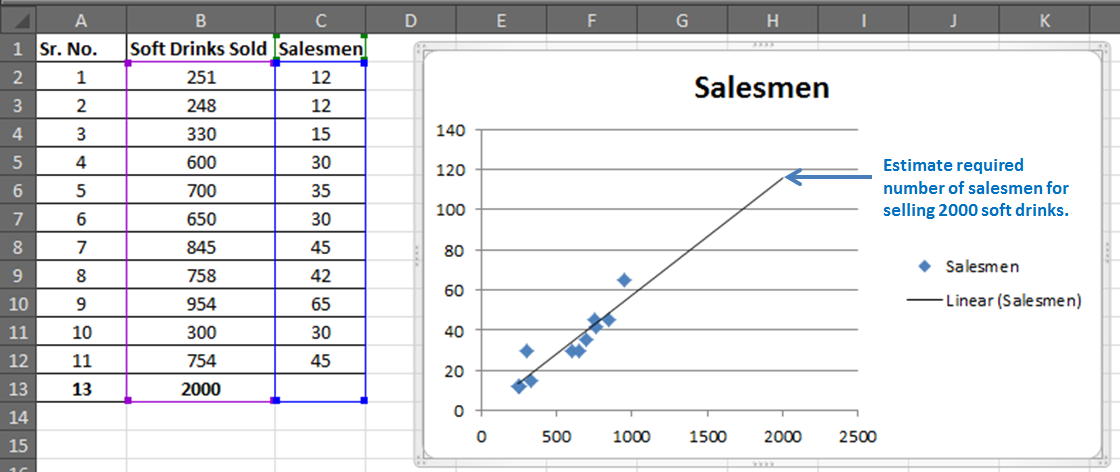
セールスマンとソフトドリンクの販売記録は11件あります。
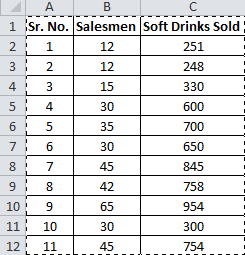
ここで、このデータに基づいて、清涼飲料の2000の販売を達成するために必要なセールスマンの数を予測します。

回帰方程式は、そのような厳密な推定を行うためのツールです。そのためには、最初に回帰を知る必要があります。
Excel関数を使用した回帰分析(手動回帰検出)
この部分では、Excelの回帰手順を説明するよりも、回帰をよりよく理解できます。
はじめに:
単純線形回帰:
2つの変数間の関係の研究は、単純線形回帰と呼ばれます。 1つの変数が他の独立変数に依存している場合。従属変数は、多くの場合、Driven、Response、Target変数などの名前で呼び出されます。また、独立変数は、運転、予測変数、または単に独立変数として発音されることがよくあります。
これらの名前はそれらを明確に説明しています。
それでは、これをシナリオと比較してみましょう。 2000の売上を達成するために必要なセールスマンの数を知りたい。したがって、ここでは、従属変数はセールスマンの数であり、独立変数はソフトドリンクを販売しています。
独立変数は主にxとして示され、従属変数はyとして示されます。私たちの場合、清涼飲料はxで販売され、販売員の数はyです。
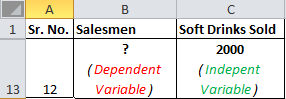
200人のセールスマンを任命した場合に販売されるソフトドリンクの数を知りたい場合は、その逆になります。
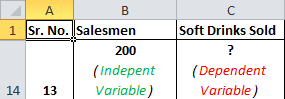
先に進みます。
線形回帰方程式の「単純な」数学:
まあ、それは簡単ではありません。しかし、Excelを使用すると簡単に実行できます。
12番目に近い予測を取得するには、11のケースすべてに必要なセールスマンの数を予測する必要があります。
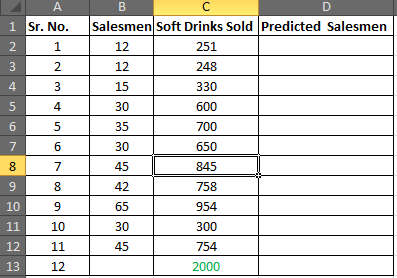
たとえば、
販売されたソフトドリンクはxです
セールスマンの数はyです
回帰方程式とも呼ばれる予測y(セールスマンの数)は
|
* (relax, I’ve got it covered) |
になります。ここで、_stat_が勾配と切片をどこで取得するのか疑問に思う必要があります。心配しないでください、Excelにはそれらのための機能があります。傾斜を見つけて手動でインターセプトする方法を学ぶ必要はありません。
必要に応じて、別のチュートリアルを用意します。コメント欄で教えてください。これらはいくつかの重要なデータ分析ツールです。
それでは、計算に移りましょう:
ステップ1:この小さなテーブルを準備する

ステップ2:回帰直線の傾きを見つける
勾配のExcel関数は
|
=SLOPE(known_y’s,known_x’s) |
ですあなたのknown_yは範囲B2:B12にあり、known_xは範囲C2:C12にあります
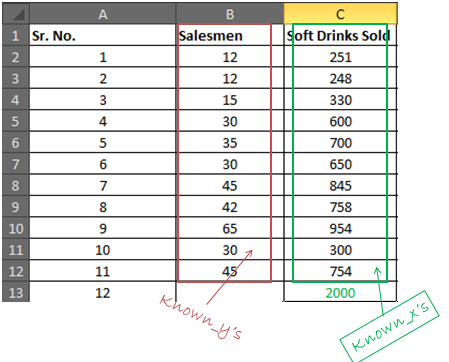
セルB16に、以下の数式を記述します
|
=SLOPE(B2:B12, C2:C12) |
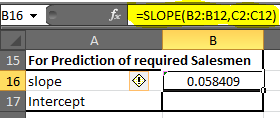
(_注:勾配は回帰方程式ではxの係数とも呼ばれます)_0.058409が得られます。小数点以下2桁に切り上げると、0.06になります。
ステップ3:回帰直線の切片を見つける
切片のExcel関数は
|
=INTERCEPT(known_y’s, known_x’s)* |
です既知のxとyが何であるかがわかっているセルB17に、この数式を書き留めます
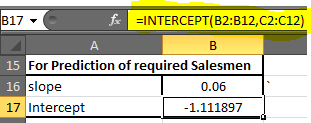
|
=INTERCEPT(B2:B12, C2:C12)* |
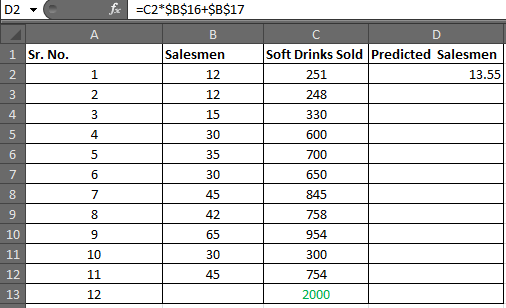
-1.1118969の値を取得します。 10進数の2桁に切り上げます。 -1.11を取得します。線形回帰方程式は= x0.06 +(-1.11)です。これで、ターゲットxに応じて可能なyを簡単に予測できます。ステップ4:* D2で、以下の式を記述します
|
=C2*$B$16+$B$17 (Regression Equation) |
13.55の値を取得します。
D2からD13を選択し、CTRL + Dを押して、D2:D13の範囲の数式を入力します
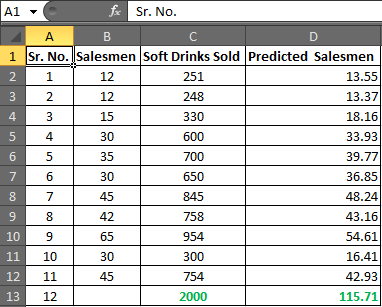
セルD13には、必要な数のセールスマンがいます。
|
Hence, to achieve the target of 2000 Soft Drink Sales, you need an estimate of 115.71 salesmen or say 116 since it is illegal to cut humans into pieces. |
これを使用すると、ExcelでWhat-If分析を簡単に実行できます。販売数を変更するだけで、その販売目標を達成するために必要な多くのセールスマンが表示されます。
それをいじって調べてください:
売上を伸ばすにはどのくらいの労働力が必要ですか?
セールスマンを増やすと、いくつの売上が増えますか?
見積もりの信頼性を高める:
これで、2000件の販売を行うには116人のセールスマンが必要であることがわかりました。
分析では、何も言われ、信じられていません。あなたはあなたの見積もりに信頼性のパーセンテージを与えなければなりません。それはあなたの方程式の証明書を与えるようなものです。